система відліку рухається щодо швидкість знайти час
задача 10007
Матеріальна точка рухається по колу з постійною кутовою швидкістю v0=π/6 рад/с. У скільки разів шлях Δs, пройдений точкою за час t = 4 с, буде більше модуля її переміщення Δr? Прийняти, що в момент початку відліку часу радіус-вектор r, що задає положення точки на колі, щодо вихідного стану був повернутий на кут φ0=π/3 рад.задача 10990
Прожектор О встановлено на відстані l = 100 м від стіни АВ і кидає світлу пляму на цю стіну. Прожектор обертається навколо вертикальної осі, роблячи один оберт за час Т = 20 с. Знайти: 1) рівняння руху світлої плями по стіні протягом першої чверті обороту; 2) швидкість v, з якою світла пляма рухається по стіні, в момент часу t = 2 с. За початок відліку прийняти момент, коли напрям променя збігається з ОС.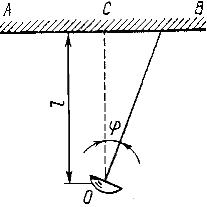
задача 11265
У лабораторній системі відліку віддаляються одна від одної дві частинки з однаковими за модулем швидкостями. Їх відносна швидкість u в тій же системі відліку дорівнює 0,5c. Визначити швидкості частинок.задача 11567
Ліфт почав підніматися з постійним прискоренням w = 1,00 м/с2. Через час t = 1,00 см від стелі кабіни ліфта відокремився і став падати шуруп. Визначити: а) час Δt падіння шурупа до удару об підлогу кабіни, б) шлях s, пройдений шурупом за час Δt в системі відліку, пов'язаній з Землею. Висота кабіни ліфта h = 2,75 м.задача 12528
При переправі через річку шириною 60 м треба потрапити в точку, що лежить на 80 м нижче за течією, ніж точка старту. Човняр управляє моторним човном так, що він рухається точно до мети зі швидкістю 8 м/с відносно берега. Яка при цьому швидкість човна відносно води, якщо швидкість течії річки 2,8 м/с?задача 12529
При переправі через річку шириною 80 м треба потрапити в точку, що лежить на 60 м вище за течією, ніж точка старту. Човняр управляє моторним човном так, що він рухається точно до мети зі швидкістю 4,5 м/с відносно берега. Яка при цьому швидкість човна відносно води, якщо швидкість течії річки 2,1 м/с?задача 12993
Швидкість течії річки v = 3 км/ч, a швидкість руху човна щодо води v1 = 6 км/год. Визначте, під яким кутом відносно берега має рухатися човен, щоб пропливти поперек річки.задача 13168
Планета масою М рухається по колу навколо Сонця зі швидкістю v (відносно геліоцентричної системи відліку) Визначте період обертання цієї планети навколо Сонця.задача 14405
Знайти швидкість v відносно берега річки: а) човна, що йде за течією; 6) човна, що йде проти течії; в) човна, що йде під кутом ? = 90° до течії. Швидкість течії річки u = 1 м/с, швидкість човна відносно води v0 = 2 м/с.задача 16176
Деяка планета маси М рухається по колу навколо Сонця зі швидкістю v = 34,9 км/с (щодо геліоцентричної системи відліку). Знайти період обертання цієї планети навколо Сонця.задача 16177
Період обертання Юпітера навколо Сонця в 12 разів більше відповідного періоду для Землі. Вважаючи орбіти планет круговими, знайти: а) у скільки разів відстань від Юпітера до Сонця перевищує відстань від Землі до Сонця; б) швидкість і прискорення Юпітера в геліоцентричній системі відліку.задача 16318
Знайти власну довжину стрижня, якщо в лабораторній системі відліку його швидкість v = c/2, довжина l = 1,00 м і кут між ним і напрямком руху θ = 45°.задача 16320
З якою швидкістю рухався в К-системі відліку годинник, якщо за час t = 5,0 с (в К-системі) він відстав від годинника цієї системи на δt = 0,10 с?задача 16335
Дві частки рухаються назустріч один одному зі швидкостями v1 = 0,50c і v2 = 0,75c по відношенню до лабораторної системи відліку. Знайти: а) швидкість зближення частинок в лабораторній системі відліку; б) їх відносну швидкість.задача 17480
Джерело світла рухається зі швидкістю v щодо приймача. Показати, що при v << с відносна зміна частоти світла визначається формулою Δω/ω= v/c·cosθ.задача 18199
Моторний човен, рухаючись за течією річки, проходить 120 м і через 1,5 хв повертається назад. Швидкість течії річки 3,6 км/год. Визначити швидкість човна відносно води.задача 19868
Власний час життя частинки дорівнює 10–6 с. Визначити час життя цієї частки в системі відліку, щодо якої вона рухається зі швидкістю 0,99c. (c — швидкість світла).задача 20533
Човен рухається щодо води зі швидкістю, в півтора рази меншою швидкості течії річки. Під яким кутом до напрямку течії човен повинен тримати курс, щоб його знесло течією якомога менше?задача 20534
Човен рухається щодо води зі швидкістю, в два рази меншою швидкості течії річки. Під яким кутом до напрямку течії човен повинен тримати курс, щоб його знесло течією якомога менше?задача 20535
Моторний човен рухається щодо води зі швидкістю в два рази більшою за швидкість течії річки. Під яким кутом до напрямку течії човен повинен тримати курс, щоб його знесло течією якомога менше?задача 21910
На моторному човні, що рухається проти течії річки зі швидкістю v0 щодо берега, несподівано заглох двигун. Як надалі буде рухатися човен, якщо сила опору води Fc = βvотн (vотн — швидкість човна відносно води)? Швидкість течії всюди постійна і дорівнює v1.задача 23269
По перетинаючих під кутом 60° дорогах рухається два автомобілі з постійними швидкостями 20 м/с та 25 м/с. Визначити модуль та напрямок швидкості одного автомобіля щодо іншого. Визначити, через який час після зустрічі відстань між машинами дорівнюватиме 1000 м?задача 24078
Дві частки рухаються назустріч одна одній зі швидкостями v1 = 0,5c і v2 = 0,75c щодо лабораторної системи відліку. Знайдіть швидкість зближення частинок в лабораторній системі відліку і відносну швидкість часток.задача 25060
В системі K' знаходиться квадрат, сторона якого паралельна осі x'. Визначити кут між його діагоналями у системі К, якщо система K' рухається щодо K зі швидкістю v=0,95c.задача 25900
Дві частки з однаковими швидкостями v = 3/4c (c — швидкість світла) рухаються по одній прямій і потрапляють в мішень. Одна з часток потрапила в мішень пізніше іншої на час τ = 10–8 c. Знайти відстань між частками в польоті в системі відліку, пов'язаній з ними.задача 40831
Знайти час і місце зустрічі об'єктів 1 і 3, якщо x1 = 250–10t, x3 = –100+10t.Другие предметы