прослизання радіус маса швидкість
задача 10044
Нитка з прив'язаними до її кінців вантажами масами m1 = 50 г і m2 = 60 г перекинута через блок діаметром D = 4 см. Визначити момент інерції J блоку, якщо під дією сили тяжіння вантажів він отримав кутове прискорення ε = 1,5 рад/с2. Тертям і проковзуванням нитки по блоку знехтувати.задача 10050
До кінців легкої та нерозтяжної нитки, перекинутої через блок, підвішені вантажі масами m1 = 0,2 кг і m2 = 0,3 кг. У скільки разів відрізняються сили, що діють на нитку по обидві сторони від блоку, якщо маса блоку m = 0,4 кг, a його вісь рухається вертикально вгору з прискоренням α = 2 м/с2? Силами тертя і прослизання нитки по блоку знехтувати.задача 12064
Порожній циліндр котиться без проковзування по гірці. Залежність його потенційної енергії від координати Wn(x) зображена на графіку. Визначити кінетичну енергію циліндра, обумовлену рухом його центру мас, в точці "С", якщо в точці "А" повна кінетична енергія циліндра дорівнює 30 Дж.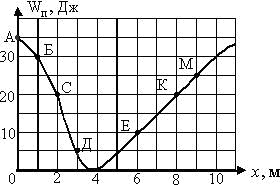
задача 14071
Обруч масою m = 0,3 кг і радіусом R = 0,5 м привели в обертання, надавши йому енергію обертального руху 1200 Дж, і відпустили на підлогу так, що його вісь обертання виявилася паралельною площині пола. Якщо обруч почав рухатися без прослизання, маючи кінетичну енергію обертання 200 Дж, то сила тертя здійснила роботу, рівну ...задача 15020
По горизонтальній площині котиться без проковзування циліндр радіусом R. Висловити декартові координати х і у деякої точки А на обід колеса через кут повороту колеса φ.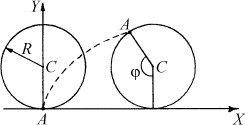
задача 15022
По опуклій циліндричній поверхні радіусом R котиться без проковзування циліндр радіусом r. Висловити кутову швидкість обертання циліндра ω через швидкість руху його центру vc.задача 16537
З гірки висотою H скочується без проковзування куля. Швидкість кулі біля основи гірки вирахували по співвідношенню: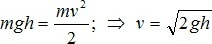 . Визначте абсолютну і відносну похибки результату.
. Визначте абсолютну і відносну похибки результату.
задача 16538
З гірки висотою h скочується без проковзування куля. Тертя дуже мале. Швидкість кулі біля основи гірки вирахували за формулою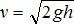 . Визначити похибку результату. Результат: 1) завищений; 2) занижений; 3) вірний.
. Визначити похибку результату. Результат: 1) завищений; 2) занижений; 3) вірний.
задача 18192
Кільце радіусом R котиться без проковзування по горизонтальній поверхні з кутовою швидкістю ω. Знайти залежність координат деякої точки А кільця (рис. 1.24) від часу, якщо в початковий момент хА = 0, уА = 0, α = 0.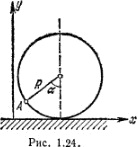
задача 19857
Суцільний однорідний циліндр радіусом r = 10 см і масою m = 2 кг скочується без проковзування з висоти 1 м уздовж похилої площини. Визначте момент імпульсу циліндра щодо осі обертання біля основи похилої площини.задача 19858
Однорідний суцільний циліндр і однорідний шар, що мають однакову масу і радіус, закочуються без прослизання на похилу площину. Знайти відношення висот, на які вони піднімуться уздовж похилої площини, якщо біля основи похилої площини їх швидкості однакові.задача 19866
Порожній циліндр котиться без проковзування по гірці. Залежність його потенційної енергії від координати Wп(x) зображена на графіку. Визначити кінетичну енергію циліндра, обумовлену обертанням, в точці "Е", якщо в точці "А" його швидкість дорівнювала нулю.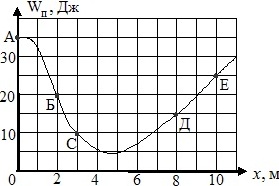
задача 20009
Однорідний суцільний циліндр масою m1 = 1 кг може обертатися без тертя навколо осі симетрії. За цю вісь він прив'язаний до бруска масою m2 = 2 кг. До бруска прикладена горизонтальна сила, рівна 20 Н. Коефіцієнт тертя бруска о площину дорівнює 0,1. Визначити прискорення циліндра, якщо він котитися без прослизання.
задача 21195
Труба радіусом 25 см котиться без проковзування по горизонтальній поверхні. Знайти модуль переміщення точки D, труби: а) за чверть обороту; б) за один оборот. Зобразити траєкторію руху цієї точки, щодо початкової точки дотику поверхні Dn.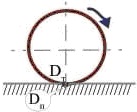
задача 22894
Обруч котиться рівномірно без прослизання. Як спрямовані вектори швидкості та прискорення точки А обруча? Вкажіть на малюнку напрямки цих векторів.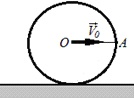
задача 23398
Однорідний диск зі стану спокою скочується без прослизання з похилої площини, висота якої h = 0,5 м. Визначте лінійну швидкість руху центру диска біля основи похилої площини і максимальну лінійну швидкість руху точок, що знаходяться на обід диска, біля основи похилої площини (в м /с).задача 23410
Суцільна і порожниста кулі, що мають однакові маси та радіуси, скочуються без ковзання з гірки висотою h. Яке з тіл матиме велику швидкість біля основи гірки та у скільки разів?задача 23414
Куля масою m = 3 кг скочується без ковзання з вершини похилої площини висотою h = 4 м без початкової швидкості. Довжина ската похилої площини l = 8 м, а значення коефіцієнта тертя кочення тіла однаково протягом усього шляху μ = 0,1. Знайдіть відстань, яка пройде кулю від підніжжя похилої площини до повної зупинки.задача 25073
Циліндр радіусом R та масою М без початкової швидкості скочується з похилої площини з кутом при основі α. Знайти прискорення циліндра і який має бути коефіцієнт тертя щоб не було прослизання.задача 25167
Куля масою 0,25 кг котиться горизонтальною поверхнею без прослизання зі швидкістю 4,0 м/с. Визначити її повну кінетичну енергію.задача 26316
Однорідний шар котиться без проковзування по гірці. Залежність його потенційної енергії від координати w1(x) зображена на графіку. Визначити кінетичну енергію кулі, обумовлену рухом його центру мас, в точці "Д", якщо в точці "А" повна кінетична енергія кулі дорівнює 10 Дж.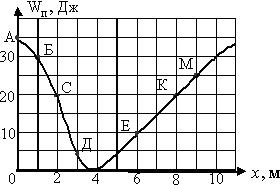
задача 26783
Однорідний шар масою 23 кг, маючи нульову початкову швидкість, починає скочуватися без прослизання з верхньої точки похилої площини висотою 3,2 м. Під час руху виділяється кількість теплоти, що дорівнює 600 Дж. Знайти швидкість кулі біля основи похилої площини.задача 40525
Кулька, маса якої m = 50 г, скочується без проковзування по жолобу з висоти h = 30 см і описує вертикальну петлю радіуса R = 10 см. З якою силою кулька тисне на жолоб у нижній і верхній точках петлі по нормалі до неї?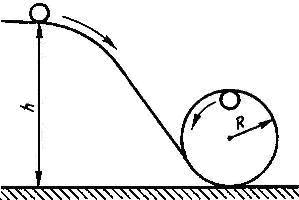
Другие предметы