однорідний радіус момент інерції маса відносно вісі проходить центр через знайти
задача 10548
Через блок радіусом R = 3 см перекинули шнур, до кінців якого прив'язані вантажі масами m1 = 100 г і m2 = 120 г. При цьому вантажі прийшли в рух з прискоренням a = 3 м/с 2. Визначити момент інерції блоку. Тертя при обертанні не враховувати.задача 11138
Визначити момент інерції J тонкого однорідного стрижня довжиною l = 60 см і масою m = 100 г відносно осі, перпендикулярної йому і що проходить через точку стержня, віддалену на а = 20 см від одного з його кінців.задача 11141
Два однорідних тонких стрижня: АВ довжиною l1 = 40 см і масою m1 = 900 г і CD довжиною l2 = 40 см і масою l2 = 400 г скріплені під прямим кутом. Визначити момент інерції J системи стрижнів щодо осі OO', коли вісь OO' проходить через точку А перпендикулярно площині креслення.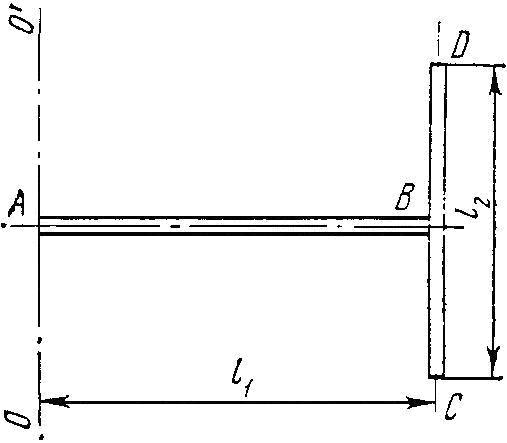
задача 11144
Знайти момент інерції J тонкого однорідного кільця радіусом R = 20 см і масою m = 100 г відносно осі, що лежить у площині кільця і проходить через його центр.задача 11145
Визначити момент інерції J кільця масою m = 50 г і радіусом R = 10 см відносно осі, дотичної до кільця.задача 11146
Діаметр диска d = 20 см, маса m = 800 г. Визначити момент інерції J диска відносно осі, що проходить через середину одного з радіусів перпендикулярно площині диска.задача 12095
Знайти момент інерції тонкого дротяного кільця радіусом а й маси m відносно осі, що збігається з його діаметром.задача 12939
Платформа у вигляді диска радіусом R = 2 м і масою m1 = 150 кг обертається за інерцією навколо вертикальної осі з частотою n = 8 хв-1. У центрі платформи стоїть людина масою m2 = 65 кг. Яку лінійну швидкість відносно Землі буде мати людина, якщо вона перейде на край платформи?задача 12946
Визначити момент інерції кільця масою m = 250 г і радіусом R = 10 см щодо осі, дотичної до кільця.задача 13063
Два однакові візки масою M кожен рухаються по інерції (без тертя) один за одним з однаковою швидкістю v0. У якийсь момент часу людина масою m, що знаходиться на задньому візку, стрибнула на передній візок зі швидкістю u відносно свого візка. Визначте швидкість v переднього візка.задача 13126
Виведіть формулу для моменту інерції циліндричної муфти відносно вісі, що збігається з її віссю симетрії. Маса муфти дорівнює m, внутрішній радіус r, зовнішній R.задача 13342
Визначте положення центру мас половини круглого диска радіусом R, вважаючи його однорідним.задача 13640
Виведіть формулу для моменту інерції тонкого кільця радіусом R і масою m відносно осі симетрії.задача 13641
Виведіть формулу для моменту інерції тонкого стрижня масою m і довжиною l щодо осі, що проходить через центр мас перпендикулярно його довжині.задача 13799
Діаметр мідної кулі 0,2 м. Чому дорівнює момент інерції кулі відносно осі, що проходить на відстані 0,5 м від її центру?задача 14228
На краю нерухомої платформи масоюзадача 14318
Людина маси m1 = 80 кг знаходиться в центрі рівномірно обертова кругла платформа. Частота обертання n платформи дорівнює 0,5 с–1. На скільки Δn зміниться частота обертання платформи, якщо людина перейде з її центру в точку платформи, що знаходиться на середині радіуса. Платформу можна розглядати як суцільний однорідний диск маси m2 = 120 кг. Момент інерції людини розраховувати як для матеріальної точки.задача 14532
Чому дорівнює момент інерції тонкого стрижня довжиною 0,5 м і масою 0,2 кг відносно осі, перпендикулярної до його довжини і що проходить через точку стрижня, яка віддалена на 0,15 м від одного з її кінців?задача 14635
Махове колесо, момент інерції якого J = 245 кг·м, обертається з частотою n = 20 об/с. Через час t = 1 хв після того, як на колесо перестав діяти момент сил М, воно зупинилося. Знайти момент сил тертя Мтр і число обертів N, яке зробило колесо до повної зупинки після припинення дії сил. Колесо вважати однорідним диском.Задача 23983
Визначте момент інерції сталевого маховика щодо осі валу. Щільність стали ρ = 7800 кг/м3, радіус центрального отвору для вала r = 0,1 м, R1 = 6r, R2 = 4r, R3 = 2r, α = 45°. Плоский маховик товщиною h = 0,02 м з циліндричними вирізами. Кількість вирізів n знайдіть за формулою n = 360/α, їх радіуси рівні r.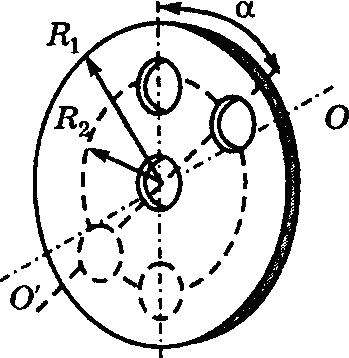
задача 14991
До обіду однорідного суцільного диска діаметром 90 см прикладена постійна дотична сила 0,1 кН, яка веде до обертання диска щодо осі, що проходить через його центр інерції. При обертанні диска на нього діє ще і момент сил тертя величиною 20 Н·м. За 5 с диск збільшує свою частоту обертання з 180 до 300 об/хв. Визначити масу диска.задача 15048
Знайти момент інерції обруча масою m і радіусом R відносно осі, що проходить через діаметр обруча.задача 15049
Знайти момент інерції полого циліндра радіусами R1 і R2 і масою m відносно осі симетрії циліндра.задача 15050
Знайти момент інерції конуса масою m і радіусом основи R відносно осі симетрії конуса.задача 16061
До кінця тонкого стрижня довжиною 1 м і масою 3 кг прикріплена маленька кулька масою 1 кг. Знайти момент інерції стрижня з кулькою щодо осі, що проходить через інший кінець стрижня.задача 16158
Ступінчастий блок з радіусами R = 2 м і r = 1 м обертається з прискоренням β = 0,2 с–2 (см. рис. 3.5). Знайти момент інерції блоку, якщо маси вантажів m1 = 4 кг, m2 = 1 кг.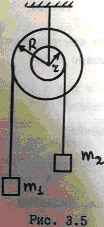
задача 16213
Платформа у вигляді диска масою 160 кг обертається за інерцією зі швидкістю 10 рад/с. На платформи стоїть людина масою 80 кг. Яка буде кутова швидкість платформи, якщо людина перейде в її центр? Вважати платформу круглим однорідним диском, а людину — точковою масою. Радіус платформи 1,5 м.задача 16536
Як зміниться момент інерції свинцевого циліндра щодо його осі, якщо його сплюснути в диск, товщина якого стала менше висоти циліндра в 10 разів?задача 17338
Людина маси m = 60 кг знаходиться на краю круглої нерухомої платформи, яка може вільно обертатися навколо вертикальної осі, що проходить через її центр. Радіус R платформи дорівнює 1 м. З якою кутовою швидкістю |ω| почне обертатися платформа, якщо людина піде по краю платформи зі швидкістю u = 2 м/с щодо платформи? Момент інерції J платформи прийняти рівним 180 кг·м2. Момент інерції людини розраховувати як для матеріальної точки.задача 17476
Знайдіть момент інерції J і момент кількості руху L земної кулі відносно осі обертання, якщо прийняти Землю за однорідну кулю масою М і радіусом R. Період обертання Землі Т.задача 17477
Знайти момент інерції і момент імпульсу земної кулі відносно осі обертання, якщо прийняти Землю за однорідну кулю масою m = 5,96·1024 кг і радіусом R = 6,37·106 м.задача 17490
Циліндр масою 5 кг і радіусом 15 см обертається навколо осі, що проходить через його центр. Рівняння обертання циліндра має вигляд: φ(t) = 1+6t2–t3, рад. Знайти закон зміни моменту сил, що діють на циліндр, їх величину в момент часу 3 с. Обчислити момент інерції циліндра, якщо вісь обертання буде проходити по його поверхні.задача 17513
Диск масою 5 кг і радіусом 10 см обертається навколо осі, що проходить через його центр. Рівняння обертання диска має вигляд φ = φ0 + 2t2 – t3, рад. Знайти закон зміни моменту сил, що діє на диск. Обчисліть момент сил в момент часу 4 с. Обчислити момент інерції диска, якщо вісь обертання буде проходити через половину радіуса.задача 17987
Порожній циліндр обертається щодо осі, що збігається з віссю циліндра. Закон обертання має вигляд φ = 10 – 5t + 0,5t2. Визначити момент інерції і масу циліндра, якщо його радіус 0,05 м. Момент сили відносно осі обертання, що діє на циліндр, 0,75 Н·м.задача 19103
Визначити момент інерції однорідного диска радіусом 20 см і масою 1 кг відносно осі, перпендикулярної площині диска і проходить через: а) центр диска; б) середину одного з радіусів диска.задача 19142
Куля масою 2 кг і радіусом 10 см обертається навколо осі, що проходить через її центр. Рівняння обертання кулі має вигляд: φ(t) = φ0 + 4t2 – t3. Знайти закон зміни моменту сил, що діють на кулю, величину їх в момент часу 2 с. Обчисліть момент інерції кулі, якщо вісь обертання буде проходити через половину радіуса.задача 19505
Визначити момент інерції диска радіусом R = 30 см з центральним отвором радіусом r = 10 см щодо осі симетрії. Маса диска m = 4 кг.задача 19914
Дві гирі масами 500 г і 600 г з'єднані легкою ниткою і перекинуті через блок, момент інерції якого 50 кг·м2 і радіус 20 см. Знайти кутову швидкість обертання блоку через 3 с після початку руху. Гальмуючий момент в осі блоку дорівнює 100 Н·м.задача 20075
На кінцях тонкого однорідного стрижня довжиною 30 см і масою 400 г закріплені вантажі масою 200 і 300 м Визначити момент інерції цього фізичного маятника і період його власних коливань щодо осі, що проходить через середину стержня.задача 20735
Дві матеріальні точки масами m розташовані симетрично щодо осі O1O1', розташованої в площині креслення. Як зміниться момент інерції цих точок при повороті осі в площині креслення на кут α = 45° з положення O1O1' в положення O2O2'.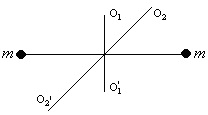
задача 20737
Визначте момент інерції дротяного рівностороннього трикутника зі стороною а = 10 см щодо осі, що збігається з однією з сторін трикутника. Маса трикутника дорівнює m = 12 г і рівномірно розподілена по довжині дроту.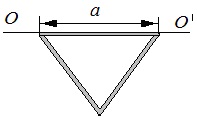
задача 21317
Одне або декілька тіл (циліндри, кулі, диски, обручі) радіусом r і масою m1 підвішені в точці А чи закріплені на стержнях масою m2 = 100 г, довжина яких l = 40 см значно перевищує їх товщину. Знайти моменти інерції J систем тіл щодо заданої осі АА'. Виконати додаткове завдання.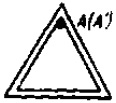
задача 21659
Порожній циліндр масою 8 кг має внутрішній діаметр 1 м, зовнішній 1,1 м. Чому дорівнює момент інерції цього циліндра щодо своєї осі?задача 21917
Знайти тензор інерції тонкої прямокутної пластини маси М зі сторонами а і b відносно осей, що проходять через центр мас пластини. Осі х і у паралельні сторонам пластини, вісь z перпендикулярна площині пластини.задача 21948
Шарик радіуса 6,2 см з пластичного матеріалу має деякий момент інерції I1. Цю кульку перетворюють в циліндр висоти 3,8 см. Момент інерції циліндра відносно його осі виявився I2. Знайти відношення I2/I1.задача 22204
Знайти момент інерції I і момент імпульсу L земної кулі відносно осі обертання. Маса Землі дорівнює m = 6·1024 кг, радіус Землі вважати рівним R = 6400 км.задача 23951
Радіус-вектор частки залежить від часу за законом: r(t) = 3ti+4t2j+5k. Знайдіть тангенс кута між вектором швидкості v та віссю х у момент часу t = 2 с.задача 24043
Знайдіть момент інерції кулі радіусом R і масою m щодо осі, що проходить через центр кулі.задача 24051
Чому дорівнює момент інерції диска I радіусом r щодо осі ГО, коли з нього вирізали диск радіусом r/2. Товщина диска b, щільність ρ.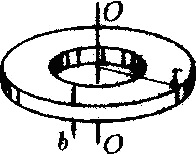
задача 24143
Вал радіусом 8 см та масою 40 кг щодо осі АА' має момент інерції (в кг·м2):
задача 24171
Знайдіть момент інерції тонкого кільця щодо осі, перпендикулярної площині кільця і яка проходить через будь-яку точку його кола. Маса кільця m, радіус кільця R.задача 24358
Кут повороту диска масою m, радіусом R = 0,7 м та моментом інерції I описується рівнянням φ = Bt2 + Ct3, де B = 0,5 с–2, C = 0,2 с–3, M = 3 Н·м — момент сил, що діють диск в момент часу t = 7 с. Знайти m.задача 24722
При розрахунку моментів інерції тіла щодо осей, які проходять через центр мас, використовують теорему Штейнера. У скільки разів збільшиться момент інерції тонкостінної трубки, якщо вісь обертання перенести з центру мас на утворюючу?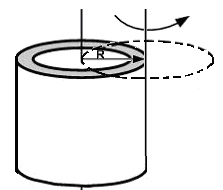
задача 24723
Момент інерції тонкого обруча масою m, радіусом R щодо осі, що проходить через центр обруча перпендикулярно площині, в якій лежить обруч, дорівнює J = mR2. Як зміниться момент інерції обруча, якщо вісь обертання перенести паралельно до точки на обручі?задача 24724
Визначте скільки разів зміниться момент інерції тонкого однорідного стрижня, якщо вісь обертання стрижня перенести з центру мас на один з його кінців (див. малюнок)?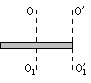
задача 24879
Диск з вирізом має масу М. Визначити момент інерції I щодо осі, що проходить через точку А перпендикулярно до площини диска.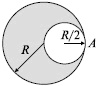
задача 24920
Чотири однакові тіла маси m кожне розташовані на площині у вершинах квадрата зі стороною L. Чому дорівнює момент інерції I цієї системи щодо осі, що проходить через одне з тіл цієї системи перпендикулярно до площини?задача 24969
Знайти момент інерції системи, що складається з колеса маси 1 кг і радіуса 0,5 м і двох стрижнів маси 0,3 кг, кожен щодо осі, що проходить через точку. О'.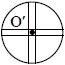
задача 25052
Тверде тіло є фізичним маятником і може здійснювати коливання у вертикальній площині біля горизонтальної осі, що проходить через точку О на ньому. Визначте: а) положення центру мас С маятника щодо точки O; б) момент інерції маятника J щодо горизонтальної осі, що проходить через точку О; в) період коливань та наведену довжину маятника. Тіло – однорідний диск масою 2m радіусу. R=40см, на кінці діаметра закріплений вантаж масою m. Положення точки О — на протилежному від вантажу кінці діаметра; положення осі - перпендикулярно площині диска.задача 25055
Тверде тіло є фізичним маятником і може здійснювати коливання у вертикальній площині біля горизонтальної осі, що проходить через точку О на ньому. Визначте: а) положення центру мас С маятника щодо точки O; б) момент інерції маятника J щодо горизонтальної осі, що проходить через точку О; в) період коливань та наведену довжину маятника. Тіло - однорідне кільце радіусу R = 40 см та масою 2m, на протилежних кінцях діаметра якого перебувають вантажі масами m і 2m. Положення точки О — на кінці діаметра з меншим вантажем, перпендикулярно площині кільця.задача 25058
Тверде тіло є фізичним маятником і може здійснювати коливання у вертикальній площині біля горизонтальної осі, що проходить через точку О на ньому. Визначте: а) положення центру мас С маятника щодо точки O; б) момент інерції маятника J щодо горизонтальної осі, що проходить через точку О; в) період коливань та наведену довжину маятника. Тіло – однорідний диск масою 2m радіусу. R=40см, на кінці діаметра закріплений вантаж масою m. Положення точки О — на протилежному від вантажу кінці діаметра, перпендикулярно площині диска.задача 26448
Визначити момент інерції кулі масою 10 кг і радіусом 20 см відносно осі, розташованої на відстані l = 0,5R від центру кулі.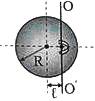
задача 26624
Балка 1 масою m1 = 200 кг лежить на валах 2 і 3, моменти інерції яких відносно осі обертання I1 = I2 = 0, 1 кг·м2. Визначити силу F, яку необхідно прикласти до балці, щоб надати їй прискорення а = 1 м/с2, якщо радіус r = 0,1 м.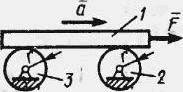
задача 26694
Платформа у вигляді суцільного диска радіусом R = 1,5 м і масою М = 180 кг обертається за інерцією близько вертикальної осі з частотою n = 10 хв -1. У центрі платформи стоїть людина масою m = 60 кг. Яку лінійну швидкість відносно підлоги матиме людина, якщо він перейде на край платформи?задача 40501
Визначте момент інерції системи, що складається з тонкого однорідного стрижня масою m = 100 г і довжиною l = 80 см і двох куль масами m1 = 400 г і m2 = 300 г, якщо перший куля закріплена на середині стрижня, a друга - на його кінці. Вісь обертання перпендикулярна стрижню і проходить через його вільний кінець. Кулі вважати матеріальними точками.задача 40675
На краю горизонтальної платформи стоїть людина масою 80 кг. Платформа являє собою круглий однорідний диск масою 160 кг, що обертається навколо вертикальної осі, яка проходить через її центр, з частотою 6 об/хв. Скільки обертів на хвилину робитиме платформа, якщо людина перейде від краю платформи до її центру? Момент інерції людини розраховувати як для матеріальної точки.задача 40737
Приймаючи людину за циліндр радіусом 20 см, висотою 1,7 м і масою 70 кг, визначити момент інерції його в положенні лежачи відносно вертикальної осі, яка проходить через коліна на відстані 55 см від стопи.задача 40782
Визначте момент інерції тонкого диска маси m = 5 кг і радіуса R = 47 см відносно осі, перпендикулярної до площини диска і що проходить через його край.Другие предметы