температура швидкість визначити інтервал часу
задача 10490
Визначити частку вільних електронів в металі при температурі T = 0 К, енергії ε яких укладені в інтервалі значень від 1/2εmax до εmax.задача 10505
Точка рухається по прямій відповідно до рівняння х = At+Bt3, де A = 6 м/с; B = 0,125 м/с3. Визначити середню швидкість <Δs/Δt> точки в інтервалі часу від t1 = 2 с до t2 = 6 с.задача 11002
Рух точки по прямій задано рівнянням x = At+Bt2, де A = 2 м/с, В = -0,5 м/с2. Визначити середню шляхову швидкість руху точки в інтервалі часу від t1 = 1 с до t2 = 3 с.задача 11035
Велосипедне колесо обертається з частотою n = 5 с–1. Під дією сил тертя воно зупинилося через інтервал часу Δt = 1 хв. Визначити кутове прискорення ε і число N обертів, яке зробить колесо за цей час.задача 11701
Електрон знаходиться в однорідному електричному полі напруженістю Е = 200 кВ/м. Який шлях пройде електрон за час t = 1 нс, якщо його початкова швидкість дорівнювала нулю? Якою швидкістю буде володіти електрон в кінці цього інтервалу часу?задача 12469
Визначте, яка частина молекул азоту при температурі t = 27°С має швидкості, модулі яких лежать в інтервалі від 210 до 215 м/с.задача 12556
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 11 м воно було два рази з інтервалом в часі 3 с.задача 12689
Газоподібний азот знаходиться в рівноважному стані при нормальних умовах. Знайти відносне число молекул, що мають позитивні проекції швидкості vx в інтервалах від 60 до 65 м/с і від 300 до 305 м/с. Пояснити отриманий результат.задача 12702
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 10 м воно було два рази з інтервалом в часі 4 с. Опір повітря не враховувати.задача 12703
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 11 м воно було два рази з інтервалом в часі 4 с. Опір повітря не враховувати.задача 12704
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 11 м воно було два рази з інтервалом в часі 5 с. Опір повітря не враховувати.задача 12705
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 12 м воно було два рази з інтервалом в часі 4 с. Опір повітря не враховувати.задача 12706
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 14 м воно було два рази з інтервалом в часі 3 с. Опір повітря не враховувати.задача 12707
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 15 м воно було два рази з інтервалом в часі 2 с. Опір повітря не враховувати.задача 12708
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 15 м воно було два рази з інтервалом в часі 3 с. Опір повітря не враховувати.задача 12709
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 15 м воно було два рази з інтервалом в часі 4 с. Опір повітря не враховувати.задача 12710
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 17 м воно було два рази з інтервалом в часі 5 с. Опір повітря не враховувати.задача 12711
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 18 м воно було два рази з інтервалом в часі 3 с. Опір повітря не враховувати.задача 12712
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 19 м воно було два рази з інтервалом в часі 4 с. Опір повітря не враховувати.задача 12713
Визначити початкову швидкість, з якою тіло кинуто вертикально вгору, якщо на висоті 20 м воно було два рази з інтервалом в часі 4 с. Опір повітря не враховувати.задача 13011
Залежність пройденого тілом шляху від часу задається рівнянням s = A−Bt + Ct² + Dt³ (A = 6 м, В = 3 м/с, С = 2 м/с², D = 1 м/с³). Визначте для тіла в інтервалі часу від t1 = 1 с до t2 = 4 с 1) середню швидкість, 2) середнє прискорення.задача 14102
Визначити частку Δзадача 14230
Температура кисню 208°С. Визначити відношення числа молекул цього газу, модулі швидкостей яких лежать в інтервалі 798-802 м/с, до числа молекул, модулі швидкостей яких лежать в інтервалі 398-402 м/с.задача 14231
Температура кисню 28°С. Визначити відношення числа молекул цього газу, модулі швидкостей яких лежать в інтервалі 798-802 м/с, до числа молекул, модулі швидкостей яких лежать в інтервалі 398-402 м/с.задача 14232
Температура кисню 210°С. Визначити відношення числа молекул цього газу, модулі швидкостей яких лежать в інтервалі 800-804 м/с, до числа молекул, модулі швидкостей яких лежать в інтервалі 400-404 м/с.задача 14245
Знайти число ΔN молекул кисню, що займає при нормальних умовах об'єм V = 10 мм3, швидкості яких лежать в інтервалі значень від v1 = 0 до v2 = 0,01vвер. Число Лошмідта nл = 2,69·1019 см–3 вважати відомим. На графіку Nf(v) заштрихувати площу, відповідну знайденому значенню Δзадача 14412
Тіло кинуто вертикально вгору з початковою швидкістю v0 = 9,8 м/с. Побудувати графік залежності висоти h і швидкості v від часу t для інтервалу 0 ≤ t ≤ 2 с через 0,2 с.задача 15312
Два тіла кинуті вертикально вгору з однієї точки один за одним з інтервалом часу t = 5 с і однаковими початковими швидкості v0 = 2 м/с. Через деякий час t1 відраховується від моменту кидання першого тіла, тіла зустрінуться?задача 15312
Тіло кинуто під кутом 30° до горизонту. З якою швидкістю було кинуто тіло і яка горизонтальна дальність його польоту, якщо воно перебувало в польоті 2 с? Яка максимальна висота підйому тіла? Опором повітря знехтувати.задача 15930
Рівняння руху точки має вигляд x = –270+12t. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 20 c, Δt = 2,0 c); 6) вказати характер руху точки.задача 15931
Рівняння руху точки має вигляд x = –1,5t. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 10 c, Δt = 1,0 c); 6) вказати характер руху точки.задача 15932
Рівняння руху точки має вигляд x = 2+0,4t2. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 40 c, Δt = 4,0 c); 6) вказати характер руху точки.задача 15933
Рівняння руху точки має вигляд x = 1–0,2t2. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 30 c, Δt = 3,0 c); 6) вказати характер руху точки.задача 15934
Рівняння руху точки має вигляд x = –0,4t2. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 20 c, Δt = 2,0 c); 6) вказати характер руху точки.задача 15935
Рівняння руху точки має вигляд x = 2+5t. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 50 c, Δt = 5,0 c); 6) вказати характер руху точки.задача 15936
Рівняння руху точки має вигляд x = 150–10t. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 40 c, Δt = 4,0 c); 6) вказати характер руху точки.задача 15937
Рівняння руху точки має вигляд x = 400–0,6t. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 100 c, Δt = 10,0 c); 6) вказати характер руху точки.задача 15938
Рівняння руху точки має вигляд x = 10t+0,4t2. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 20 c, Δt = 2,0 c); 6) вказати характер руху точки.задача 15939
Рівняння руху точки має вигляд x = 2t–t2. По рівнянню визначити: 1) координату х0 точки в початковий момент часу; 2) початкову швидкість v0 точки; 3) прискорення а точки; 4) написати формулу залежності швидкості від часу v = f(t); 5) побудувати графік залежності координати від часу x = f(t) і швидкості від часу v = f(t) в інтервалі 0 < t < τ з кроком Δt (τ = 15 c, Δt = 1,5 c); 6) вказати характер руху точки.задача 20454
Знайти для газоподібного азоту при Т = 300 К відношення числа молекул з компонентами швидкості уздовж осі х в інтервалі 300±0,31 м/с до числа молекул з компонентами швидкості уздовж тієї ж осі в інтервалі 500±0,51 м/с.задача 20578
На малюнку представлений графік функції розподілу молекул ідеального газу за швидкостями (розподіл Максвелла), де f(V) = dN/(N·dN) — частка молекул, швидкості яких укладені в інтервалі від V до V + dV в розрахунку на одиницю цього інтервалу. Для цієї функції вірним твердженням є … 1) При зниженні температури площа під кривою зменшується. 2) При підвищенні температури максимум кривої зміщується вліво. 3) Площа заштрихованої смужки з ростом температури буде зменшуватися. 4) Зі зменшенням температури величина максимуму зменшується.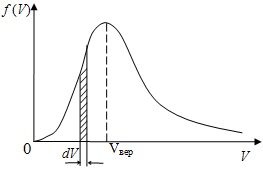
задача 20581
На малюнку представлений графік функції розподілу молекул ідеального газу за швидкостями (розподіл Максвелла), де f(V) = dN/(N·dN) — частка молекул, швидкості яких укладені в інтервалі від V до V+dV в розрахунку на одиницю цього інтервалу. Якщо, не змінюючи температури, взяти інший газ з більшою молярною масою і таким же числом молекул, то ... 1) величина максимуму зменшиться; 2) площа під кривою збільшиться; 3) площа заштрихованої смужки зменшиться; 4) максимум кривої зміститься вліво.
задача 20586
На малюнку представлений графік функції розподілу молекул ідеального газу за швидкостями (розподіл Максвелла), де f(V) = dN/(N·dN) — частка молекул, швидкості яких укладені в інтервалі від V до V+dV в розрахунку на одиницю цього інтервалу. Якщо, не змінюючи температури, взяти інший газ з меншою молярною масою і таким же числом молекул, то … 1) величина максимуму збільшиться; 2) площа під кривою зменшиться; 3) максимум кривої зміститься вправо, в бік великих швидкостей. 4) площа заштрихованої смужки зменшиться.
задача 20589
У трьох посудинах знаходяться гази, причому для температур і мас молекул газів мають місце такі співвідношення: Т1 = Т2 = Т3, m01 = m02 = 2m03. На малюнку схематично представлені графіки розподілу молекул ідеального газу за швидкостями (розподіл Максвелла) для цих газів, де f(V) = dN/(N·dV) — частка молекул, швидкості яких укладені в інтервалі від V до V+dV в розрахунку на одиницю цього інтервалу. Для графіків цих функцій вірними є твердження, що ... 1) Крива 1 відповідає розподілу за швидкостями молекул газу в посудині 2; 2) крива 3 відповідає розподілу за швидкостями молекул газу в посудині 1; 3) крива 2 відповідає розподілу за швидкостями молекул газу в посудині 2; 4) крива 3 відповідає розподілу за швидкостями молекул газу в посудині 3.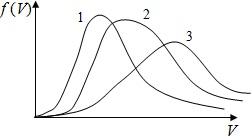
задача 20591
На малюнку представлений графік функції розподілу молекул ідеального газу за швидкостями (розподіл Максвелла), де f(V) = dN/(N·dN) — частка молекул, швидкості яких укладені в інтервалі від V до V+dV в розрахунку на одиницю цього інтервалу. Якщо, не змінюючи температури, взяти інший газ з більшою молярною масою і таким же числом молекул, то 1) величина максимуму зменшиться 2) площа під кривою збільшиться 3) максимум кривої зміститься вліво, в сторону менших швидкостей 4) максимум кривої зміститься вправо, в бік великих швидкостей.
задача 21693
За який час охолоне до температури навколишнього середовища tкон = 0 °С куля радіусом R = 5 см з матеріалу щільністю ρ = 2,6·103 кг/м3 і теплоємністю λ = 896 Дж/(кг·К), що знаходиться при температурі tнач = 500 °С. Кулю можна вважати абсолютно чорним тілом; охолодження відбувається тільки за рахунок випромінювання.задача 21694
За який час охолоне до температури навколишнього середовища tкон = 0 °С куля радіусом R = 10 см з матеріалу щільністю ρ = 7,9·103 кг/м3 і теплоємністю λ = 500 Дж/(кг·К), що знаходиться при температурі tнач = 100 °С. Кулю можна вважати абсолютно чорним тілом; охолодження відбувається тільки за рахунок випромінювання.задача 21697
За який час охолоне до температури навколишнього середовища tкон = 0 °С куля радіусом R = 8 см з матеріалу щільністю ρ = 11,3·103 кг/м3 і теплоємністю λ = 126 Дж/(кг·К), що знаходиться при температурі tнач = 100 °С. Кулю можна вважати абсолютно чорним тілом; охолодження відбувається тільки за рахунок випромінювання.задача 21701
За який час охолоне до температури навколишнього середовища tкон = 0 °С куля радіусом R = 10 см з матеріалу щільністю ρ = 2,6·103 кг/м3 і теплоємністю λ = 896 Дж/(кг·К), що знаходиться при температурі tнач = 300 °С. Кулю можна вважати абсолютно чорним тілом; охолодження відбувається тільки за рахунок випромінювання.задача 22878
Задано початкове значення радіус-вектора r1 = 4i–3j, м і кінцеве r2 = –i–2j, м описують положення рухомої матеріальної точки для моментів часу t1 = 1 c і t2 = 3 c. Намалюйте вектор переміщення точки в координатах X-Y. Знайдіть величину середньої швидкості переміщення точки за цей інтервал часу.задача 23148
Рух матеріальної точки за двома взаємно перпендикулярними напрямками визначається рівняннями: х = 5 – 2t3 (м), y = 3 + 6t2 (м). Визначити середню швидкість переміщення в інтервалі від t1 = 0 с до t2 = 3 c.задача 23351
Виходячи з розподілу Максвелла за абсолютними швидкостями, визначити середнє відносне число молекул водню при Т = 200 К, швидкості яких лежать в інтервалі (198÷202) м/с.задача 23642
Отримати залежність коефіцієнта внутрішнього тертя від температури газів. Побудувати графік залежності коефіцієнта внутрішнього тертя водню від температури в інтервалі від 100 до 600 К через кожні 100 К.задача 23643
Побудувати графік залежності коефіцієнта внутрішнього тренування азоту від температури в інтервалі 100 К ≤ Т ≤ 600 К через шкірні 100 К.задача 23818
Відомо, що людське вухо сприймає пружні хвилі в інтервалі частот від ν1 = 20 Гц до ν2 = 20 кГц. Яким довжинам хвиль відповідає цей інтервал у повітрі? У воді? Швидкості звуку у повітрі у воді рівні відповідно υ1 = 340 м/с і υ2 = 1400 м/с.задача 24459
Знайдіть, при якій температурі число молекул азоту, швидкості яких лежать в інтервалі 299 - 301 м/с, дорівнює кількості молекул зі швидкостями в інтервалі 599 - 601 м/с?задача 24602
У деякому інтервалі температур ν молей газу, які займають об'єм V0, розширюються так, що температура газу змінюється згідно із законом Т = aV–bV2, де a та b задані константи. Визначте роботу газу при збільшенні його об'єму θ рази. Намалюйте графік процесу на р, V діаграмі. Чи цей процес є політропним?задача 24603
У деякому інтервалі температур ν молей газу, які займають об'єм V0, розширюються так, що температура газу змінюється згідно із законом Т = aV–bV2, де a та b задані константи. Визначте роботу газу зі збільшенням його об'єму вдвічі. Намалюйте графік процесу на р, V діаграмі. Чи цей процес є політропним?задача 24820
При вимірі опору власного напівпровідника було встановлено, що за температури t1 його опір дорівнює R1 = 5657 Ом, а при температурі t2 = 57°С дорівнюε R2 = 3428 Ом. ΔE = 0,32 еВ — ширина забороненої зони. 1. Знайдіть t1. 2. Побудуйте графік залежності опору напівпровідника від температури в інтервалі від t2 до t1 з кроком Δt = 3°С. 3. Знайдіть значення температурного коефіцієнта опору напівпровідника за температури t2 і t1. 4. Використовуючи довідкові таблиці, визначте назву напівпровідника.задача 40656
Рух точки задано рівнянням х = At + Bt2, де А = 4м/с, В = –0,05 м/с2 . Побудувати графіки залежності шляху, переміщення, швидкості і прискорення точки в інтервалі часу від t1 = 0 до t2 = 80с.задача 40884
З високої вежі з інтервалом t = 1 с кидають з нульовою початковою швидкістю два камені. На якій відстані s один від одного знаходитимуться камені в той момент, коли швидкість другого стане рівною 30 м/с?Другие предметы