точка здійснює два гармонійні коливання визначити рівняння знайти
задача 10073
Точка здійснює прості гармонійні коливання, рівняння яких x = Asinωt, де А = 5 см, ω = 2 с. B момент часу, коли точка володіла потенційною енергією П = 0,1 мДж, на неї діяла повертаюча сила F = 5 мН. Знайти цей момент часу t.задача 10074
Визначити частоту ν простих гармонійних коливань диска радіусом R = 20 см біля горизонтальної осі, що проходить через середину радіуса диска перпендикулярно його площині.задача 10075
Визначити період Т простих гармонійних коливань диска радіусом R = 40 см біля горизонтальної осі, що проходить через творчу диска.задача 10566
Точка здійснює гармонійні коливання, рівняння яких має вигляд х = A sin ωt, де A = 5 см; ω = 2 с. B момент, коли на точку діяла повертаюча сила F = +5 мН, точка мала потенційну енергію П = 0,1 мДж. Знайти цей момент часу t і відповідну йому фазу φ коливання.задача 10568
Матеріальна точка масою m = 0,01 кг здійснює гармонійні коливання, рівняння яких має вигляд х = А sinωt, де A = 0,2 м; ω = 8π с–1. Знайти повертаючу силу F в момент часу t = 0,1 с, a також повну енергію Е точки.задача 10571
Визначити період Т простих гармонійних коливань диска радіусом R = 30 см біля горизонтальної осі, що проходить через творчу диска.задача 10574
Точка здійснює одночасно два гармонійних коливання, що відбуваються по взаємно перпендикулярним напрямам і які висловлюються рівняннями: x = A1cos ω1t і y = A2sin ω2t, де А1 = 1 см; ω1 = 0,5 с–1; A2 = 1 см; ω2 = 1 с–1. Знайти рівняння траєкторії, побудувати її з дотриманням масштабу і вказати напрямок руху.задача 11308
Точка здійснює гармонійні коливання. Найбільше зміщення xmax точки дорівнює 10 см, найбільша швидкість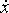
max = 20 см/с. Знайти кутову частоту ω коливань і максимальне прискорення 
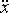max точки.
задача 11321
Точка здійснює одночасно два гармонійних коливання, що відбуваються по взаємно перпендикулярним напрямам і виражаються рівняннями x = A1cosωt і y = A2cosω(t+τ), де А1 = 4 см, A1 = 8 см, ω = π c–1, τ = 1 с. Знайти рівняння траєкторії точки і побудувати графік її руху.задача 11322
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються за взаємно перпендикулярними напрямами, які виражаються рівняннями: 1) x = Acosωt і y = Acosωt; 2) x = Acosωt і y = A1cosωt; 3) x = Acosωt і y = Acos(ωt+φ1); 4) x = A2cosωt и y = Acos(ωt+φ2); 5) x = A1cosωt і y = A1sinωt; 6) x = Acosωt і y = A1sinωt; 7) x = A2sinωt і y = A1sinωt; 8) x = A2sinωt і y = Asin(ωt+φ2). Знайти (для восьми випадків) рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 11324
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, які виражаються рівняннями x = A1cosωt і y = A2sinωt, де A1 = 2 см, A2 = 1 см. Знайти рівняння траєкторії точки і побудувати її, вказавши напрямок руху.задача 12238
Рівняння гармонійних коливань дано у вигляді: Х = 0,2cos (2πt + π/3), м. Знайти, яку частку становить кінетична енергія від повної енергії в момент часу t = T/6.задача 12270
Точка виконує гармонічні коливання відповідно до рівняння x = 0,4 sinπt (м). Визначити швидкість і прискорення точки через 1/6 c від початку коливань.задача 12277
Гармонійні коливання в контурі описуються рівнянням: q = 10–9cos(104t+π/2), Кл. Записати рівняння коливань напруги на пластинах конденсатора і струму. Ємність конденсатора дорівнює С = 0,1 нФ.задача 12552
Точка бере участь одночасно в двох гармонійних коливаннях, що відбуваються у взаємно перпендикулярних напрямках і описуваних рівняннями х = cos πt і у = cos πt/2. Визначити рівняння траєкторії точки і накреслити її з нанесенням масштабу.задача 12874
Матеріальна точка, яка здійснює гармонічні коливання з частотою ν = 1 Гц, в момент часу t = 0 проходить положення, яке визначається координатою х0 = 5 см, зі швидкістю v0 = –15 см/с. Визначте амплітуду коливань.задача 12875
Матеріальна точка, яка здійснює гармонічні коливання з частотою ν = 2 Гц, в момент часу t = 0 проходить положення, яке визначається координатою х0 = 6 см, зі швидкістю v0 = 14 см/с. Визначте амплітуду коливань.задача 13637
Точка здійснює гармонічні коливання за законом x = 3cos(πt/2+π/8), м. Визначте: 1) період коливань, 2) максимальну швидкість vmax точки; 3) максимальне прискорення аmаx точки.задача 13639
Швидкість матеріальної точки, що здійснює гармонічні коливання, задається рівнянням v(t) = -6sin 2πt. Запишіть залежність зміщення цієї точки від часу.задача 13644
Тіло масою m = 10 г здійснює гармонійні коливання за законом х = 0,1 cos(4t + π/4), м. Визначте максимальні значення: 1) повертаючої сили, 2) кінетичної енергії.задача 13645
Матеріальна точка масою m = 50 г здійснює гармонійні коливання згідно рівняння x = 0,1 cos(3πt/2), м. Визначте: 1) повертаючу силу F для моменту часу t = 0,5 с; 2) повну енергію E точки.задача 13646
Матеріальна точка масою m = 20 г здійснює гармонійні коливання за законом х = 0,1 cos(4πt + π/4) м. Визначте повну енергію E цієї точки.задача 13648
Визначте відношення кінетичної енергії Т точки, що здійснює гармонічні коливання, до її потенційної енергії П, якщо відома фаза коливання.задача 13688
Точка бере участь одночасно в двох гармонічних коливаннях, що відбуваються у взаємно перпендикулярних напрямках і описуваних рівняннями x = 3 cos 2ωt, см і у = 4 cos(2ωt + π), см. Визначте рівняння траєкторії точки і викресліть її з нанесенням масштабу.задача 13690
Точка бере участь одночасно в двох гармонічних коливаннях, що відбуваються у взаємно перпендикулярних напрямках і описуваних рівняннями x = A sin(ωt+π/2), y = A sin ωt. Визначте рівняння траєкторії точки і накресліть її з нанесенням масштабу, вказавши напрямок її руху по цій траєкторії.задача 13692
Точка бере участь одночасно в двох гармонічних коливаннях, що відбуваються у взаємно перпендикулярних напрямках і описуваних рівняннями x = A sin ωt і у = A sin 2ωt. Визначте рівняння траєкторії точки і викресліть її з нанесенням масштабу.задача 13768
Один кінець пружного стрижня з'єднаний з джерелом гармонійних коливань, що підкоряються закону ξ = A cosωt, a другий його кінець жорстко закріплений. Враховуючи, що відображення в місці закріплення стрижня походить від менш щільного середовища, визначте характер коливань в будь-якій точці стрижня.задача 14001
Матеріальна точка масою m = 0,05 кг здійснює гармонійні коливання, рівняння яких має вигляд: х = 0,1 sin (5t) м. Знайти силу F, що діє на точку: 1) в момент, коли фаза коливання φ = 30°, 2) в положенні найбільшого відхилення точки.задача 14021
Повна енергія тіла, що здійснює гармонійні коливання, дорівнює 30 мкДж, максимальна сила, що діє на тіло, дорівнює 1,5 мН. Написати рівняння руху цього тіла, якщо період коливань дорівнює 2 с, а початкова фазa дорівнює нулю.задача 14125
Рука людини при ходьбі здійснює гармонійні коливання за рівнянням x = 17sin1,6πt см. Визначити час проходження руки від положення рівноваги до максимального відхилення.задача 14358
Рівняння гармонійних коливань тіла має вигляд x = 5sin π(t+0,1), см. Чому рівні період і циклічна частота цих коливань?задача 15028
В процесі гармонійних коливань грузик математичного маятника має максимальну швидкість 3 м/с і максимальне прискорення 3,14 м/с2. Чому дорівнює період коливань маятника?задача 15488
Повна енергія тіла, що здійснює гармонійний коливальний рух, W = 30 мкДж; максимальна сила, що діє на тіло, Fmax = 1,5 мН. Написати рівняння руху цього тіла, якщо період коливань T = 2 с і початкова фаза φ = π/3.задача 15575
Період гармонійних коливань математичного маятника зменшується в 2 рази. На скільки відсотків зросте при цьому частота коливань?задача 15696
Побудуйте в зошиті графіки і спектри гармонійних коливань, заданих наступними часовими залежностями: x1 = 2 sin πt, х2 = sin 2πt. Виконайте додавання цих коливань, розташуйте графіки точно один під іншим. Побудуйте спектри коливань.задача 15927
Визначити повну енергію точки масою 20 г, що здійснює гармонічні коливання x = 0,15cos(4πt+π/5) (м), а також визначити силу, що діє на точку в момент часу t = 0,2 с.задача 15967
Математичний маятник масою m = 100 г і довжиною l = 1 м здійснює гармонійні коливання за законом x = 2,5sin2πt см. Визначити натяг в момент часу t = T/4.задача 16105
По заданому рівнянню x = 20 cos 2πt (см) гармонійних коливань пружинного маятника визначити основні параметри коливальної системи (xm, ω, ν, T, k), намалювати графіки залежності координати, швидкості і прискорення від часу. m = 10 г.задача 17925
Частка бере участь в двох гармонійних коливаннях, що проходять уздовж одного напрямку. Частота однакова для обох коливань і дорівнює 9 Гц, початкові фази мають значення π/6 рад і 0 рад, амплітуди відповідно рівні 7 см і 4 см. Запишіть рівняння вихідних коливань. Знайдіть амплітуду і початкову фазу результуючого коливання, запишіть його рівняння.задача 18129
Матеріальна точка здійснює гармонічні коливання. Найбільше зміщення точки 25 см, максимальна швидкість 50 см/с. Знайти максимальне прискорення точки і її зміщення через 2 с.задача 18130
Матеріальна точка масою 0,2 кг здійснює гармонійні коливання, рівняння яких має вигляд х = A sin ωt, де А = 0,4 м; ω = 30 рад/с. Знайти повну енергію точки і повертаючу силу в момент часу 0,2 с.задача 18134
Максимальна сила, що діє на тіло, яке здійснює гармонійне коливання, дорівнює 2·10–3 Н, повна енергія дорівнює 5·10–5 Дж. Написати рівняння руху цього тіла, якщо період коливань 3 с і початкова фаза 30°.задача 18953
Точка бере участь одночасно в двох гармонійних коливаннях, що відбуваються у взаємно перпендикулярних напрямках і описуваних рівняннями х = 3cosωt, см і у = 4cosωt, см. Визначте рівняння траєкторії точки і викресліть її з нанесенням масштабу.задача 19608
Математичний маятник масою m = 10 г і довжиною l = 10 м здійснює гармонійні коливання за законом α = 0,25·sin2πt. Визначити силу натягу в момент часу t = T/2.задача 19945
Матеріальна точка здійснює гармонічні коливання за законом x = xmsinω0t. Графік, на якому зображена залежність проекції прискорення ax цієї точки від часу t, наведено під номером ...
задача 19950
Точка здійснює одночасно два гармонійних коливання, що відбуваються по взаємно перпендикулярних напрямках і виражаються рівняннями x = 4cosπt см і y = 8cos(πt+π) см. Знайдіть рівняння траєкторії точки і побудуйте графік її руху.задача 19955
Матеріальна точка здійснює коливання за законом x = xmcosω0t. Залежність проекції vx швидкості цієї точки від часу t наведена на графіку під номером ...
задача 20109
Точка здійснює гармонійні коливання з частотою 10 Гц. B момент, прийнятий за початковий, точка мала максимальне зміщення 1 мм. Написати рівняння коливань точки і накреслити їх графік.задача 21121
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються у взаємно перпендикулярних напрямках. Рівняння коливань х = A cos ωt і у = A cos (ωt + φ). Визначити рівняння траєкторії точки у вигляді f(x, у) = 0. Прийняти А = 2 см, φ = π/2.задача 21409
Точка здійснює одночасно два гармонійних коливання, що відбуваються по взаємно перпендикулярних напрямках і виражаються рівняннями х = 4 cos πt см і у = 2 sin π(t + 1) см. Знайти рівняння траєкторії точки і побудувати графік її руху.задача 21744
Рівняння коливань звучного камертона має вигляд: Δр(t) = 0,003sin(800πt), Па. Звук, що видається камертоном, поширюється в повітрі у вигляді плоскої хвилі при нормальному атмосферному тиску і температурі 17° С. Обчисліть швидкість поширення хвилі і звуковий тиск в точці М, що знаходиться на відстані 10 м від камертона через 0,03 с після початку коливань. Газ вважати двоатомним з молярною масою 29 кг/кмоль.задача 21756
Написати рівняння руху x (t) частки, що одночасно бере участь у двох коливаннях одного напрямку: x1 = 30cos πt/3 і x2 = 30cos(πt/3 + π/6) (мм).задача 21985
Точка масою 5 г здійснює гармонійне коливання закону x = 5sin(3/5πt + π/3) (см). Написати рівняння коливань кінетичної і потенційної енергії точки: визначити повну енергію точки.задача 22014
Матеріальна точка бере участь одночасно в двох гармонійних коливаннях, що проходять уздовж однієї прямої. В одиницях СІ рівняння доданків коливань записуються у вигляді x1 = 0,1cos π(t+1/6) и x2 = 0,05cos π(t+1/2). Визначити рівняння результуючих коливань.задача 22015
Матеріальна точка бере участь одночасно в двох гармонійних коливаннях, що проходять уздовж однієї прямої. В одиницях СІ рівняння доданків коливань записуються у вигляді x1 = 0,1cos πt/2 і x2 = 0,12 cos π(t+1)/2. Визначити рівняння результуючих коливань.задача 22141
Рівняння гармонійних коливань має вигляд х = Acos(ωt). Відомо, що при фазі π/6 рад змішання дорівнює 2 см. Визначити змішання і швидкість точки при фазі 3π/4 рад, якщо період коливань Т = 2 с.задача 22191
Повна енергія тіла, що здійснює гармонійні коливання, дорівнює 45 мкДж, максимальна сила, що діє на тіло, дорівнює 2 мН. Написати рівняння руху цього тіла, якщо період коливань дорівнює 3 с і початкова фаза 30° (косинусоидальной залежність).задача 22225
Рівняння коливань у ніжки звучного камертона має вигляд: Δр(t) = 0,003sin(800πt), Па. Звук, що видається камертоном, поширюється в повітрі (μ = 29 кг/кмоль) при нормальному атмосферному тиску і температурі 17 ° С. Визначити: 1) швидкість поширення хвилі; 2) звуковий тиск в точці М, що знаходиться на відстані y(M) = 10 м від камертона через t = 0,03 с після початку коливань. Газ вважати двоатомним (γ = 7/5), хвилю плоскою.задача 22635
Матеріальна точка бере участь одночасно в двох гармонійних коливаннях, що проходять уздовж однієї прямої. В одиницях СІ рівняння доданків коливань записуються у вигляді x1 = 0,1cos πt/2 и x2 = 0,12cos π(t+1)/2. Визначити рівняння результуючих коливань.задача 22843
Матеріальна точка здійснює гармонічні коливання. Найбільше зміщення точки дорівнює xmax = 10 см, а максимальна швидкість υmax = 20 см/с. Визначити циклічну частоту коливань ω і максимальне прискорення amax точки.задача 23448
Матеріальна точка масою m = 20 г здійснює гармонічні коливання згідно із законом х = 0,2 cos(2πt + π/6) м. Визначити максимальне значення швидкості частки vmax та повну енергію W цієї точки.задача 23455
Матеріальна точка маси m = 10 г під дією пружної сили здійснює гармонічні коливання згідно із законом х = Аcos(ω0t + φ0), де А = 5,0 см, ω0 = 3 рад/с, φ0 = π рад. Визначити модуль пружної сили, що діє на матеріальну точку в момент часу t = 3 після початку коливань.задача 23457
Крапка здійснює одночасно два гармонійні коливання, що відбуваються за взаємно перпендикулярними напрямками і виражаються рівняннями х = А1cos ωt і у = А2cos ω(t + τ), де А1 = 4 см, А2 = 8 см, ω = π с–1, τ = 1 с. Знайти рівняння траєкторії точки та побудувати її з дотриманням масштабу, вказавши напрямок руху точки. Поясніть свою відповідь.задача 23471
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються за взаємно перпендикулярними напрямками і виражаються рівняннями: x = 2cos ωt см і y = cos ωt см. Запишіть рівняння траєкторії результуючого руху точки і побудуйте її з дотриманням масштабу.задача 23609
Визначити натяг нитки в момент t, якщо математичний маятник масою m, довжиною l здійснює гармонічні коливання за заданим законом а = а0 sin(ωt + φ).задача 24057
Повна енергія тіла, що здійснює гармонійний коливальний рух, дорівнює 30 мкДж; максимальна сила, що діє тіло, дорівнює 1,5 мН. Написати рівняння руху цього тіла, якщо період коливань дорівнює 2 с і початкова фаза дорівнює π/3.задача 24098
Точка здійснює коливання, що описуються рівнянням: x = 5 sin(0,1πt), см. У певний момент часу сила, що діє на точку, та її потенційна енергія відповідно рівні 2·10–2 Н і 5·10–4 Дж. Чому рівні фаза коливань та кінетична енергія точки в цей момент часу?задача 24506
Матеріальна точка здійснює гармонічні коливання, рівняння яких має вигляд х = 0,05 sin (2t + π/4) м. Визначити період коливань, а також момент часу (найближчий до початку відліку), коли потенційна енергія точки дорівнює Wp = 1·10–4 Дж, а повертаюча сила F = 5·10–3 Н.задача 24735
Точка здійснює гармонійні коливання. Найбільше зміщення точки дорівнює 10 см, максимальна швидкість 20 см/с. Знайти кутову частоту коливань та максимальне прискорення точки.задача 24736
Наведено рівняння гармонійних коливань чотирьох систем з різними коефіцієнтами пружності k та однаковими масами m. У якому разі коефіцієнт пружності найменший? Підтвердьте ваш вибір розрахунками. 1) х = 2 cos(3πt + π), см 2) х = 3 cos(2πt + π), см 4) х = 3 cos(5πt + π/2), см 8) х = 4 cos(4πt + π/2), см.задача 24738
Матеріальна точка здійснює гармонійні коливання згідно із законом косинуса. Знайти відношення кінетичної енергії Wk точки, до її потенційної енергії Wp для моментів часу t = T/12, t = T/8 і t = T/6.задача 25181
Крапка здійснює одночасно два гармонійні коливання, що відбуваються у взаємно перпендикулярних напрямках за рівняннями: х = A cos 2ωt і у = A1 cos ωt. Визначити рівняння траєкторії точки. Прийняти: А = 2 см; А1 = 3 см.задача 26197
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються у взаємно перпендикулярних напрямках, які виражаються рівняннями x = Acosωt і y = Acosωt. Знайти рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 26198
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються по взаємно перпендикулярним напрямам, що виражаються рівняннями x = Acosωt і y = A1cosωt. Знайти рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 26199
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються по взаємно перпендикулярним напрямам, що виражаються рівняннями x = Acosωt і y = Acos(ωt+φ1). Знайти рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 26200
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються по взаємно перпендикулярним напрямам, що виражаються рівняннями x = A2cosωt і y = Acos(ωt+φ2). Знайти рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 26201
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються по взаємно перпендикулярним напрямам, що виражаються рівняннями x = A1cosωt і y = A1sinωt. Знайти рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 26202
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються по взаємно перпендикулярним напрямам, що виражаються рівняннями x = Acosωt і y = A1sinωt. Знайти рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 26203
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються по взаємно перпендикулярним напрямам, що виражаються рівняннями x = A2sinωt і y = A1sinωt. Знайти рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 26204
Точка здійснює одночасно два гармонійних коливання однакової частоти, що відбуваються по взаємно перпендикулярним напрямам, що виражаються рівняннями x = A2sinωt и y = Asin(ωt+φ2). Знайти рівняння траєкторії точки, побудувати її з дотриманням масштабу і вказати напрямок руху. Прийняти: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.задача 26322
Точка здійснює одночасно два гармонійних коливання, що відбуваються за взаємно перпендикулярними напрямами і виражаються рівняннями: x = sin ωt/2; y = cosωt. Знайти рівняння траєкторії точки і побудувати графік її руху.задача 26535
Тіло масою 10 г здійснює гармонійні коливання за законом x = 0,1cos(4πt+π/4), м. Визначте максимальні значення: 1) повертаючої сили; 2) кінетичної енергії.задача 26671
Визначити повертає силу F в момент часу t = 0,2 c і повну енергію Е точки масою m = 20 г, що здійснює гармонічні коливання згідно рівняння х = A·sin (ωt), де А = 0,15 м і ω = 4π с-1.задача 40142
Математичний маятник масою m = 100 г і довжиною l = 1 м здійснює гармонійні коливання за законом α = 0,25sin2πt. Визначити натяг в момент часу t = T/2.задача 40604
Чому дорівнює відношення кінетичної енергії точки, що здійснює гармонічні коливання, до її потенційної енергії для моменту часу t = T/12, де Т – період коливань.задача 40631
Матеріальна точка масою m = 0,01 кг здійснює гармонійні коливання, рівняння яких має вигляд x = 0,2 sin 8πt (довжина виражена в сантиметрах, час — в секундах). Знайти повертаючу силу F в момент часу t = 0,1 с, а також повну енергію Е точки.задача 40717
Повна енергія тіла масою 1 кг, що здійснює гармонійні коливання, дорівнює 10 Дж, максимальна повертаюча сила, що діє на тіло становить 100 Н. Написати рівняння коливального руху тіла, якщо початкова фаза дорівнює 45°.задача 40781
Повна енергія тіла, що здійснює гармонійні коливання, дорівнює Е = 3·10–5 Дж. Максимальна сила, що діє на тіло, дорівнює F = 1,5·10–3 Н. Написати рівняння руху цього тіла, якщо період коливань дорівнює Т = 2 с і початкова фаза 60°.Другие предметы