точка рухається по колу радіусом визначити повне нормальне тангенціальне прискорення знайти швидкість у момент часу після початку руху
задача 10006
Тіло кинуто під кутом α=30º до горизонту зі швидкістю v0=30 м/с. Які будуть нормальне αn і тангенціальне ατ прискорення тіла через час t = 1 с після початку руху?задача 10010
Точка рухається по колу радіусом R = 30 см з постійним кутовим прискоренням ε. Визначити тангенціальне прискорення аτ точки, якщо відомо, що за час t = 4 с вона зробила три оберти і в кінці третього обороту її нормальне прискорення an=2,7 м/с2.задача 10503
Матеріальна точка рухається по колу радіуса R = 2 м згідно рівняння S = At+Bt3, де А = 8 м/с; B = –0,2 м/с3. Знайти швидкість v, тангенціальне at, нормальне an і повне a прискорення в момент часу t = 3 с.задача 10507
Диск радіусом R = 0,2 м обертається згідно з рівнянням φ = А+Bt+Ct3, де А = 3 рад; B = –1 рад/с; C = 0,1 рад/с3. Визначити тангенціальне aτ, нормальне an і повне a прискорення точок на окружності диска для моменту часу t = 10 с.задача 10508
По дузі кола радіуса R = 10 м обертається точка. B деякий момент часу нормальне прискорення точки an = 4,9 м/с2, вектор повного прискорення утворює в цей момент з вектором нормального прискорення кут α = 60°. Знайти швидкість v і тангенціальне прискорення aτ точки.задача 10776
Однорідне електричне (E = 1000 В / м) і магнітне (H = 1000 А / м) поля збігаються за напрямком. Визначити нормальне an і тангенціальне аτ прискорення протона, що рухається в цих полях у напрямку силових ліній зі швидкістю v = 8·105 м/с. Визначити також an і aτ в момент входження протона в поля з тією ж швидкістю, якби він рухався перпендикулярно силовим лініям.задача 11007
Точка рухається по кривій з постійним тангенціальним прискоренням аτ = 0,5 м/с2. Визначити повне прискорення а точки на ділянці кривої з радіусом кривизни R = 3 м, якщо точка рухається на цій ділянці зі швидкістю v = 2 м/с.задача 11008
Точка рухається по колу радіусом R = 4 м. Початкова швидкість v0 точки дорівнює 3 м/с, тангенціальне прискорення аτ = 1 м/с2. Для моменту часу t = 2 с визначити: 1) довжину шляху s, пройденого точкою; 2) модуль переміщення |Δr|; 3) середню шляхову швидкість; 4) модуль вектора середньої швидкості |<v>|.задача 11012
Точка движется по окружности радиусом R = 8,00 м. В момент времени t1 нормальное ускорение точки аn = 4,00 м/с2;, а вектор полного ускорения а образует с вектором нормального ускорения аn угол α = 50,0°. Найти скорость v и тангенциальное ускорение аτ точки в этот момент времени t1.задача 11013
Точка рухається по колу радіусом R = 2 м згідно рівняння ξ = At3, де A = 2 м/с3. У який момент часу t нормальне прискорення аn точки дорівнюватиме тангенціальному аτ. Визначити повне прискорення а в цей момент.задача 11026
Камінь кинули з вишки в горизонтальному напрямку з початковою швидкістю v0 = 30 м/с. Визначити швидкість v, тангенціальне аτ і нормальне аn прискорення каменю в кінці другої секунди після початку руху.задача 11027
Тіло кинуто під кутом α = 30° до горизонту. Знайти тангенціальне аτ і нормальне аn прискорення в початковий момент руху.задача 11032
Диск радіусом r = 10 см, що знаходився в стані спокою, почав обертатися з постійним кутовим прискоренням ε = 0,5 рад/с2. Знайти тангенціальне аτ, нормальне аn і повне а прискорення точок на окружності диска в кінці другої секунди після початку обертання.задача 11033
Диск радіусом r = 20 см обертається згідно з рівнянням φ = A+Bt+Сt3, де A = 3 рад, В = -1 рад/с, С = 0,1 рад/с3. Визначити тангенціальне аτ нормальне аn і повне а прискорення точок на окружності диска для моменту часу t = 10 с.задача 11151
Однорідний диск радіусом R = 10 см може вільно обертатися навколо горизонтальної осі, перпендикулярної до площини диска і що проходить через точку О на ньому. Диск відхилили на кут α і відпустили. Визначити для початкового моменту часу кутове ε і тангенціальне аτ прискорення точки В, що знаходиться на диску. Обчислення виконати для наступних випадків: 1) a = R, b = R/2, α = π/2; 2) a = R/2, b = R, α = π/6; 3) a = 2/3R, b = 2/3R, α = 2/3π.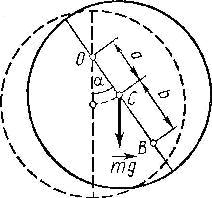
задача 11210
Точка рухається по колу радіусом 60 см з постійним тангенційним прискоренням. Знайти нормальне прискорення точки через 3 с після початку руху, якщо відомо, що до кінця п'ятого обороту після початку руху лінійна швидкість точки дорівнює 5 м/с.задача 12100
Матеріальна точка починає рухатися по колу радіусом R = 6 м з кутовим прискоренням ε = At, де А — постійна. Знайти шлях S, пройдений точкою до моменту часу, коли її тангенціальне і нормальне прискорення стануть рівними один одному.задача 12243
Камінь кинули з вишки в горизонтальному напрямку зі швидкістю 20 м/с. Визначити швидкість, тангенціальне і нормальне прискорення каменю в кінці другої секунди після початку руху.задача 12245
З вежі висотою 49 м в горизонтальному напрямку кинуто важке тіло зі швидкістю 5 м/с. Визначити тангенціальне і нормальне прискорення тіла в точці, що відповідає половині всього часу падіння тіла. Встановити, на якій відстані від башти воно впало.задача 12246
З вежі висотою 25 м в горизонтальному напрямку кинуто тіло зі швидкістю 5 м / с. Визначити тангенціальне і нормальне прискорення тіла в точці, що відповідає половині всього часу падіння тіла. Встановити, на якій відстані від башти впало тіло?задача 12267
Нормальне прискорення точки, що рухається по колу радіусом 4 м, задається рівнянням an = At3 (A = 0,5 м/с5). Визначити: 1) тангенціальне прискорення точки в момент часу 5 c; 2) шлях, пройдений точкою за час 5 с після початку руху; 3) повне прискорення для моменту часу 1 с.задача 12612
Використовуючи дані попередньої задачі, визначити: 1) частоту обертання диска у момент часу t2 в об/с і об/хв; 2) в момент часу t2 визначити швидкість, нормальне, тангенціальне і повне прискорення точок, що знаходяться на відстані 10 см від осі обертання.Дані з попередньої задачі: t2 = 15 с; ω(t2) = 11,8 рад/с; β(t2) = 1,1 рад/с2.
Попередня задача: Диск обертається згідно з рівнянням φ = а + bt + ct2 + dt3, де φ — кут повороту радіуса у радіанах, t — час у секундах. Визначити кутову швидкість і прискорення у моменти часу t1 = 11 с і t2 = 15 с. Які середні значення кутової швидкості і кутового прискорення у проміжку часу від t1 = 11 до t2 = 15 с включно, якщо для Вашого варіанту а = 1, b = 2 с–1, с = 0,1 с–2, d = 0,01 с–3?
задача 13018
Нормальне прискорення точки, що рухається по колу радіусом r = 4 м, задається рівнянням аn = А + Bt + Ct² (А = 1 м/с², В = 6 м/с³, С = 9 м/с4). Визначте: 1) тангенціальне прискорення точки; 2) шлях, пройдений точкою за час t1 = 5 с після початку руху; 3) повне прискорення для моменту часу t2 = 1 с.задача 13020
Залежність пройденого тілом шляху по окружності радіусом r = 3 м задається рівнянням s = At² + Bt (A = 0,4 м/с, В = 0,1 м/с). Визначте для моменту часу t = 1 с після початку руху прискорення: 1) нормальне, 2) тангенціальне; 3) повне.задача 13030
Точка рухається по колу радіусом R = 15 см с постійним тангенціальним прискоренням аτ. До кінця четвертого обороту після початку руху лінійна швидкість точки v1 = 15 см/с. Визначте нормальне прискорення аn2 точки через t2 = 16 с після початку руху.задача 13089
Матеріальна точка масою m = 20 г рухається по колу радіусом R = 10 см з постійним тангенціальним прискоренням. До кінця п'ятого обороту після початку руху кінетична енергія матеріальної точки виявилася рівною 6,3 мДж. Визначити тангенціальне прискорення.задача 13144
На однорідний суцільний циліндричний вал радіусом R = 5 см і масою М = 10 кг намотана легка нитка, до кінця якої прикріплений вантаж масою m = 1 кг. Визначити: 1) залежність s(t), згідно з якою рухається вантаж; 2) силу натяжіння нитки Т; 3) залежність φ(t), згідно якої обертається вал; 4) кутову швидкість ω вала через t = 1 с після початку руху; 5) тангенціальне (аτ) і нормальне (аn) прискорення точок, що знаходяться на поверхні валу.задача 13260
Маховик діаметром 18 см обертається на осі електродвигуна з частотою 20 об/с. Після відключення електричного струму маховик разом з ротором електродвигуна зробив 120 обертів і зупинився. Знайти і написати закон зміни кутової швидкості маховика, і закони зміни нормального і тангенціального прискорення (для точок, що лежать на ободі маховика) від часу.задача 13286
Рух точки по колу задано рівнянням S = 2t3. Як змінюється з часом кут між векторами повного і тангенціального прискорень точки?задача 13305
Матеріальна точка починає рухатися по колу радіусом r = 12,5 см з постійним тангенціальним прискоренням аτ = 0,5 см/с2. Визначте: 1) момент часу, при якому вектор прискорення а утворює з вектором швидкості v кут α = 45°; 2) шлях, пройдений за цей час рухомою точкою.задача 13307
Диск радіусом R = 10 см обертається навколо нерухомої осі так, що залежність кута повороту диска від часу задається рівнянням φ = A + Bt + Ct2 + Dt3 (B = 1 рад/с, С = 1 рад/с2, D = 1 рад/с3). Визначте для точок на ободі диска до кінця другої секунди після початку руху 1) тангенціальне прискорення аτ; 2) нормальне прискорення an; 3) повне прискорення а.задача 13318
Диск обертається навколо нерухомої осі так, що залежність кута повороту радіуса диска від часу задається рівнянням φ = At2 (А = 0,5 рад/с2). Визначте на кінець другої секунди після початку руху: 1) кутову швидкість диска; 2) кутове прискорення диска; 3) для точки, яка знаходиться на відстані 80 см від осі обертання, тангенціальне аτ, нормальне аn і повне а прискорення.задача 13322
Диск радіусом R = 10 см обертається так, що залежність кута повороту радіуса диска від часу задається рівнянням φ = A + Bt3 (А = 2 рад, B = 4 рад/с3). Визначте для точок на ободі колеса 1) нормальне прискорення ап в момент часу t = 2 с; 2) тангенціальне прискорення для цього ж моменту; 3) кут повороту φ, при якому повне прискорення становить з радіусом колеса кут α = 45°.задача 13816
Точка рухається по колу так, що залежність шляху від часу задається рівнянням: S = А + Bt +Ct2, де В = –2 м/с і С = 1 м/с2. Знайти лінійну швидкість точки, її тангенціальне, нормальне і повне прискорення через 3 с після початку руху, якщо відомо, що нормальне прискорення в момент часу 2 с становить 0,5 м/с2.задача 14141
Знайти нормальне, тангенціальне і повне прискорення електрона на довільній стаціонарній орбіті в іоні Не+.задача 14431
Камінь кинули горизонтально зі швидкістю vx = 15 м/с. Знайти нормальне аn і тангенціальне аτ прискорення каменю через час t = 1 с після початку руху.задача 14437
Тіло кинуто зі швидкістю v0 = 14,7 м/с під кутом α = 30° до горизонту. Знайти нормальне an і тангенціальне aτ прискорення тіла через час t = 1,25 с після початку руху.задача 14452
Точка рухається по колу радіусом R = 20 см з постійним тангенціальним прискоренням aτ = 5 см/с2. Через який час t після початку руху нормальне прискорення an точки буде: а) дорівнювати тангенціальному; б) удвічі більше тангенціального?задача 14453
Точка рухається по колу радіусом R = 10 см з постійним тангенціальним прискоренням а τ. Знайти тангенціальне прискорення аτ точки, якщо відомо, що до кінця п'ятого обороту після початку руху лінійна швидкість точки v = 79,2 см/с.задача 14454
Точка рухається по колу радіусом R = 10 см з постійним тангенціальним прискоренням а τ. Знайти нормальне прискорення аn точки через час t = 20 с після початку руху, якщо відомо, що до кінця п'ятого обороту після початку руху лінійна швидкість точки v = 10 см/с.задача 14456
Колесо радіусом R = 10 см обертається з кутовим прискоренням ε = 3,14 рад/с2. Знайти для точок на ободі колеса до кінця першої секунди після початку руху: а) кутову швидкість ω; б) лінійну швидкість v; в) тангенціальне прискорення аτ; г) нормальне прискорення аn; д) повне прискорення а; е) кут α, що складається вектором повного прискорення з радіусом колеса.задача 14457
Точка рухається по колу радіусом R = 2 см. Залежність шляху від часу дається рівнянням s = Ct3, де С = 0,1 см/с3. Знайти нормальне a n і тангенціальне aτ прискорення точки в момент, коли лінійна швидкість точки v = 0,3 м/с.задача 14458
Точка рухається по колу так, що залежність шляху від часу дається рівнянням s = A–Bt+Ct2, де В = 2 м/с і С = 1 м/с2. Знайти лінійну швидкість v точки, її тангенціальне аτ, нормальне аn і повне а прискорення через час t = 3 с після початку руху, якщо відомо, що при t' = 2 c нормальне прискорення точки а'n = 0,5 м/с2.задача 14461
Колесо радіусом R = 0,1 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням ? = А + Bt + Ct3, де В = 2 рад/с і С = 1 рад/c3. Для точок, що лежать на ободі колеса, знайти через час t = 2 с після початку руху: а) кутову швидкість ω; б) лінійну швидкість v; в) кутове прискорення ε; г) тангенціальне аτ і нормальне аn прискорення.задача 14465
У скільки разів нормальне прискорення аn точки, що лежить на ободі колеса, більше її тангенціального прискорення аτ для того моменту, коли вектор повного прискорення точки становить кут аn = 30° з вектором її лінійної швидкості?задача 14519
Тіло масою m = 10 г рухається по колу радіусом R = 6,4 см. Знайти тангенціальне прискорення аτ тіла, якщо відомо, що до кінця другого обороту після початку руху його кінетична енергія Wк = 0,8 мДж.задача 14528
Камінь кинули горизонтально зі швидкістю 15 м/с. Визначити тангенціальне і нормальне прискорення каменю через 1,0 с після початку руху, радіус кривизни траєкторії в цей момент часу. Який кут утворює вектор повного прискорення з вектором швидкості при t = 1,0 с?задача 14700
Рух точки по колу радіуса R = 4 м задано рівнянням: S = A+Bt+Ct2. Визначити тангенціальне, нормальне і повне прискорення точки в момент часу t = 2 с, якщо А = 10 м, В = –2 м/с і С = 1 м/с2.задача 14861
Заряджена частинка рухається в однорідному магнітному полі по гвинтовій лінії. Чи відмінні від нуля проекції прискорення частинки: а) тангенційна, б) нормальна?задача 15007
Точка рухається по колу радіусом R = 1,20 м. Рівняння руху точки має вигляд: φ = At + Bt3, де А = 0,500 рад/с, В = 2,50 рад/с3. Визначити тангенціальне аτ, нормальне ап і повне a прискорення точки в момент часу t = 0,954 с.задача 15008
Тіло кинуто зі швидкістю v0 = 50,0 м/с під кутом α = 40,0° до горизонту. Нехтуючи опором повітря, визначити для моменту часу t = 5,40 с після початку руху нормальне ап і тангенціальне аτ прискорення.задача 15246
Тіло кинуто під кутом 60° до горизонту з початковою швидкістю 20 м/с. Визначити координати точок на траєкторії тіла, в яких нормальне прискорення дорівнює тангенціальному.задача 15569
З вишки кинули камінь в горизонтальному напрямку. Через проміжок часу t = 2 c камінь впав на відстані S = 20 м від підстави вишки. Визначити тангенціальне прискорення каменю в кінцевій точці траєкторії.задача 15623
Матеріальна точка рухається по колу радіуса 80 см за законом S = 10t–0,1t3 (шлях в метрах, час у секундах). Знайти швидкість, тангенціальне, нормальне і повне прискорення через 2 с після початку руху.задача 15940
Колесо радіусом R = 0,2 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 5 рад/с і С = 6 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 2,5 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15941
Колесо радіусом R = 0,15 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 3 рад/с і С = 4 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 1,5 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15942
Колесо радіусом R = 0,25 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 7 рад/с і С = 3 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 3,0 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15943
Колесо радіусом R = 0,1 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 2 рад/с і С = 8 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 2,0 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15944
Колесо радіусом R = 0,5 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 3 рад/с і С = 4 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 3,0 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15945
Колесо радіусом R = 0,3 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 1 рад/с і С = 7 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 1,5 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15946
Колесо радіусом R = 0,45 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 4 рад/с і С = 2 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 3,0 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15947
Колесо радіусом R = 0,5 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 1 рад/с і С = 3 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 2,5 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15948
Колесо радіусом R = 0,25 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct3, де В = 5 рад/с і С = 4 рад/с3. Знайти для точок, що лежать на ободі колеса через t = 1,5 сек після початку руху: 1) кутову швидкість; 2) лінійну швидкість; 3) кутове прискорення; 4) тангенціальне прискорення; 5) нормальне прискорення; 6) повне прискорення.задача 15996
За проміжок часу τ = 10,0 с точка пройшла половину кола радіуса R = 160 см. Обчислити за цей час: а) середню швидкість (v), б) модуль середнього вектора швидкості |<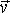 >|; в) модуль середнього вектора повного прискорення |<
>|; в) модуль середнього вектора повного прискорення |<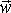 >|, якщо точка рухалася з постійним тангенціальним прискоренням.
>|, якщо точка рухалася з постійним тангенціальним прискоренням.
задача 16135
Колесо обертається так, що залежність кута повороту радіуса колеса від часу визначається рівнянням φ(t) = 1 + 2t – 2t3, рад. Нормальне прискорення точок, що лежать на ободі колеса до кінця другого секунди руху, дорівнює 200 м/с2. Обчисліть:1) залежність лінійної і кутової швидкостей, лінійного і кутового прискорень від часу;
2) радіус колеса;
3) кутову швидкість і прискорення, тангенціальне і повне прискорення в кінці 2-ої секунди руху.
задача 16311
Диск обертається так, що залежність кута повороту радіуса диска від часу визначається рівнянням: φ(t) = 2 + 4t – 4t3 (рад). Нормальне прискорення точок, що лежать на ободі колеса до кінця другого секунди руху, дорівнює 250 м/с. Визначити: 1) залежність лінійних і кутових швидкостей і прискорень від часу; 2) радіус диска; 3) кутову швидкість і прискорення (тангенціальне і повне) в кінці другої секунди руху.задача 16464
Електрон, зі швидкістю v = 106 м/с , рухається в однорідному магнітному полі перпендикулярно його лініям індукції. Визначити нормальне an і тангенціальне aτ прискорення електрона, якщо індукція магнітного поля B = 0,1 мТл.задача 17399
Кількість теплоти Q, що виділилася за 4,4 с, при постійній щільності струму в провіднику перерізом S = 4 мм2 довжиною l = 16 м, склало 20,8 Дж. Визначити заряд q, що пройшов через провідник за цей час, і тангенціальну складову напруженості електричного поля, якщо його провідність σ дорівнює 5,7·106 Ом–1·cм–1.задача 17509
Знайти нормальне і тангенціальне прискорення тіла в початковий момент часу і через 2 с після початку руху в полі сили тяжіння в разі якщо тіло кинуто з початковою швидкістю v0 = 10 м/с, під кутом 60° до горизонту з висоти 40 м.задача 17555
Точка починає рухатися по колу радіуса R = 16,0 м з тангенціальним прискоренням аτ = 10 м/с2. 1. Чому дорівнює повне прискорення точки через три секунди t = 3 с після початку руху? Рішення поясніть малюнком. 2. Чому дорівнює величина кутової швидкості та кутового прискорення при цьому русі в цей момент часу?задача 17617
Матеріальна точка рухається по площині. Рух точки в векторному вигляді описується рівнянням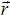 (t) =
(t) = 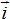 At3 +
At3 + 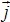 Bt (
Bt (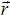 — радиус-вектор,
— радиус-вектор, 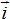 ,
, 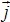 — одиничні орти відповідно по осях ОХ і OY). Написати залежність вектора швидкості від часу
— одиничні орти відповідно по осях ОХ і OY). Написати залежність вектора швидкості від часу 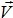 =
= 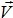 (t). Знайти в момент часу t = 1 с після початку руху: 1) модуль швидкості; 2) модуль тангенціального прискорення; 3) модуль нормального прискорення; 4) модуль повного прискорення, якщо А = 0,1 м/с3, В = 1 м/с.
(t). Знайти в момент часу t = 1 с після початку руху: 1) модуль швидкості; 2) модуль тангенціального прискорення; 3) модуль нормального прискорення; 4) модуль повного прискорення, якщо А = 0,1 м/с3, В = 1 м/с.
задача 19559
Рівняння траєкторії матеріальної точки має вигляд x2+y2 = A2, де А = 2 м, а залежність шляху від часу задається виразом S = (Bt2+Ct+D), де В = 2 м/с2, C = 1 м/с, D = 1 м. Знайти швидкість, нормальне і тангенціальне прискорення через t1 = 1 с.задача 19827
Матеріальна точка рухається по колу радіусом R = 4 м. Закон її руху описується рівнянням ξ = A+Bt2, де A = 8 м, B = –2 м/с2, а ξ відраховується вздовж окружності. Знайти момент часу, коли нормальне прискорення точки дорівнює 9 м/с2, а також швидкість, тангенціальне і повне прискорення точки в цей момент часу.задача 19828
Обертання колеса задається рівнянням φ(t) = A+Bt+Ct3, де A = 3 рад, B = 2 рад/с, C = 1 рад/с3. Радіус колеса дорівнює 1 м. Для точки, що лежить на ободі колеса, знайти через t = 3 с після початку руху кутову і лінійну швидкості, кутове, тангенціальне і нормальне прискорення.задача 19831
Матеріальна точка рухається по колу радіуса R = 2 м. Закон її руху описується рівнянням ξ(t) = At2 + Bt3, де А = 3 м/с2, В = 1 м/с3, а координата ξ(t) відраховується вздовж окружності. Знайти момент часу, коли тангенціальне прискорення точки дорівнює 18 м/с2, а також нормальне і повне лінійне прискорення точки в цей момент часу.задача 19927
Однорідний диск, що має вагу Р = 124 Н, обертається з постійним кутовим прискоренням, і його рух описується рівнянням φ = 30t2+ 2t + 1. Диск обертається під дією постійної дотичної тангенціальної сили Fτ = 90,2 Н, прикладеної до обода диска. Визначити момент сил тертя Мтр, діючих на диск при обертанні. Радіус диска R = 0,15 м.задача 19975
Тіло рухається по криволінійній траєкторії. Пройдений шлях змінюється з часом за законом s = 2 + 0,5t2, м. Визначити нормальне, тангенціальне і повне прискорення при t = 1 с. Радіус кривизни траєкторії руху в цей момент часу дорівнює 50 см. Яка середня швидкість за 1 с руху?задача 19977
Матеріальна точка почала обертатися з постійним кутовим прискоренням з положення 1 і через 0,1 с виявилася в положенні 2. Знайти кутові прискорення і швидкість в точці 2. Вказати напрямки тангенціального, нормального і повного прискорень, а також лінійної і кутової швидкостей для положення 2.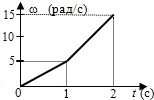
задача 20067
Матеріальна точка рухається по колу діаметром 40 м. Залежність її координати від часу руху визначається рівнянням S = t3+4t2–3t+8. В який момент точка змінює напрямок руху? Визначити пройдений шлях, швидкість, нормальне, тангенціальне і повне прискорення рухомої точки через 4 с після початку руху.задача 20115
Камінь кинули горизонтально зі швидкістю v0 = 20 м/с. Знайти радіус кривизни траєкторії каменю через 2 с після початку руху. Чому рівні в цей момент нормальне і тангенціальне прискорення?задача 20159
Частка зі стану спокою почала рухатися по дузі окружності радіусом R = 2 м з кутовою швидкістю, модуль якої змінюється з плином часу за законом ω = 2t2. Ставлення нормального прискорення до тангенціальному через 2 секунди дорівнює ... 1) 1; 2) 2; 3) 4; 4) 8.задача 20205
Матеріальна точка починає рухатися за годинниковою стрілкою по колу радіусом R = 10 см з постійним тангенціальним прискоренням аτ = 0,4 см/с2. Через проміжок часу t вектор повного прискорення а утворює з вектором миттєвої швидкості v кут β = 60°. Визначити t.задача 20206
Матеріальна точка починає рухатися за годинниковою стрілкою по колу радіусом R = 20 см з постійним тангенціальним прискоренням аτ. Через проміжок часу t = 5,0 с вектор повного прискорення а утворює з вектором миттєвої швидкості v = 0,02 м/с угол β. Визначити a.задача 20207
Матеріальна точка починає рухатися за годинниковою стрілкою по колу радіусом R = 30 см з постійним тангенціальним прискоренням аτ = 0,5 см/с2. Через проміжок часу t вектор повного прискорення а утворює з вектором миттєвої швидкості v кут β = 45°. Визначити v.задача 20208
Матеріальна точка починає рухатися за годинниковою стрілкою по колу радіусом R з постійним тангенціальним прискоренням аτ. Через проміжок часу t = 6,5 с вектор повного прискорення а = 0,8 см/с2 утворює з вектором миттєвої швидкості v = 0,03 м/с угол β. Визначити β.задача 20209
Матеріальна точка починає рухатися за годинниковою стрілкою по колу радіусом R = 50 см з постійним тангенціальним прискоренням аτ = 0,5 см/с2. Через проміжок часу t вектор повного прискорення а = 0,9 см/с2 утворює з вектором миттєвої швидкості v угол β. Визначити v.задача 20300
Частка зі стану спокою почала рухатися по дузі кола радіуса R = 1 м з постійним кутовим прискоренням ε = 2 с–2. Ставлення нормального прискорення до тангенціальному через одну секунду дорівнює ...задача 20389
Матеріальна точка рухається по колу радіуса R, причому φ = ωt (φ – кут між радіус-вектором точки, проведеним з деякою точки А окружності, і прямої, що з'єднує точку А і центр окружності; ω — константа). Знайти тангенціальну і нормальну складові швидкості і прискорення точки.задача 20390
Матеріальна точка рухається по параболі у = kх2 так, що її прискорення паралельно осі у, а його модуль постійний і дорівнює w. Визначити нормальну і тангенціальну складові прискорення точки як функції часу.задача 20424
Камінь кинули під кутом 60° до горизонту зі швидкістю 19,6 м/с. Визначити нормальне і тангенціальне прискорення каменю через 1 с після початку руху. Через скільки часу, після початку руху нормальне прискорення каменю буде максимальним?задача 20452
Матеріальна точка рухається по колу. Закон руху має вигляд s(t) = A + Bt +Ct2, A = –1 м, В = 4,5 м/с, С = –1,1 м/с2. Знайти залежність лінійної швидкості і тангенціального прискорення точки від часу. Визначити координати s, швидкість v і прискорення а, які матиме точка в момент часу t = 2 с. Який шлях пройде точка за цей час? Побудувати графіки залежності s(t), v(t) і a(t) в інтервалі від t = 0 с до t = 4 с.задача 21021
Диск радіуса R починає обертатися зі стану спокою в горизонтальній площині навколо осізадача 21100
Велосипедист і пішохід рухаються в одну сторону з однієї точки кругового треку, радіус якого 30,6 м, зі швидкостями vв = 7,22 м/с і vп = 1,51 м/с. В який момент часу: а) учасники руху виявляться в діаметрально протилежних точках трека; б) велосипедист вперше обжене пішохода? Скільки разів велосипедист обжене пішохода, поки той пройде одне коло?задача 21411
Матеріальна точка рухається по колу. Закон руху має вигляд s(t) = A + Bt + Ct2, А = –2 м, В = –3 м/с, С = 1 м/с2. Знайти залежність лінійної швидкості і тангенціального прискорення точки від часу. Визначити координату s, швидкість v, і прискорення аτ, які матиме точка в момент часу t = 1,5 c. Який шлях пройде точка за цей час? Побудувати графіки залежності s(t), v(t) і aτ(t) в інтервалі від t = 0 с до t = 4 с.задача 21501
Зміни координат матеріальної точки по двох взаємно перпендикулярних напрямах описується рівняннями x(t) = 10cos3t, y(t) = 10sin3t м. Обчисліть: 1) залежність швидкості і прискорення від часу; 2) величину швидкості, нормального і тангенціального прискорень; 3) рівняння траєкторії руху точки і характер руху точки, радіус кривизни траєкторії; 4) модуль переміщення за чверть періоду.задача 21514
Матеріальна точка масою 1 г рухається по колу радіусом 1 м відповідно до рівняння S = 8t – 0,2t3. Визначте швидкість, тангенціальне прискорення, нормальне прискорення в момент часу t = 2 с.задача 21656
До кінця десятого обороту крісла каруселі досягли швидкості 20 м/с. З яким тангенціальним прискоренням рухаються крісла, радіус обертання яких 4,9 м?задача 21791
Які нормальне і тангенціальне прискорення електрона, що рухається в співпадаючих по напрямку електричному і магнітному полях? Розглянути випадки: а) швидкість електрона спрямована вздовж полів; б) швидкість електрона спрямована перпендикулярно до них.задача 21800
Матеріальна точка рухається по колу. Закон руху має вигляд s(t) = А + Вt + Сt2, А = 1 м, В = 2 м/с, С = –3 м/с2. Знайти залежність лінійної швидкості і тангенціального прискорення точки від часу. Визначити координату s, швидкість v і прискорення аτ, які матиме точка в момент часу t = 3 с. Який шлях пройде точка за цей час? Побудувати графіки залежності s(t), v(t) і аτ(t) в інтервалі від t = 0 с до t = 4 с.задача 21905
Автомашина рухається з постійним тангенціальним прискоренням ατ = 0,62 м/с по горизонтальній поверхні, описуючи коло радіуса R = 40 м. Коефіцієнт тертя ковзання між колесами машини і поверхнею k = 0,2. Який шлях пройде машина без ковзання, якщо в початковий момент її швидкість дорівнює нулю?задача 22129
Камінь кинули під кутом 60° до горизонту зі швидкістю 19,6 м/с. Які будуть нормальне і дотичне прискорення каменю через 0,5 с після початку руху? Через скільки часу після початку руху нормальне до траєкторії прискорення каменю буде максимальним?задача 22187
Точка рухається по колу радіусом 79 см з постійним тангенціальним прискоренням. Знайти нормальне прискорення точки через 3 с після початку руху, якщо відомо, що до кінця п'ятого обороту після початку руху лінійна швидкість точки дорівнює 3 м/с.задача 22203
Точка рухається по колу радіусом R = 0,1 м з постійним тангенціальним прискоренням. Знайти прискорення точки через 10 секунд після початку руху, якщо відомо, що до кінця п'ятого обороту після початку руху лінійна швидкість точки v = 0,8 м/с.задача 22431
З вежі висотою H = 25 м горизонтально кинуто камінь зі швидкістю V0 = 15 м/с. Знайти тангенціальне і нормальне прискорення каменю через час t = 1 с після початку польоту.задача 22807
Рух точки по колу радіусом R = 2 м задано рівнянням φ = A+Bt+Ct2, де А = 10 м, В = –3 м/с, С = 2 м/с2. Знайти тангенціальне, нормальне і повне прискорення точки в момент часу t = 2 с.задача 22891
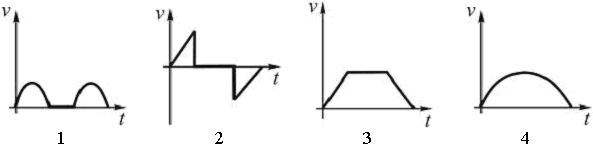
Тангенційне прискорення точки змінюється згідно з графіком. Виберіть графік залежності швидкості від часу, який відповідає такому руху. Відповідь обґрунтуйте. Побудуйте схематично графік залежності координати від часу.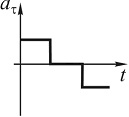
задача 22892
Точка М рухається спіраллю в напрямку, вказаному стрілкою. Нормальне прискорення за величиною не змінюється. Визначте, як змінюються у цьому русі величини тангенціального і повного прискорень точки? Поясніть вашу відповідь.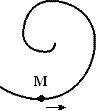
задача 22960
Частка рухається так, що її радіус-вектор змінюється згідно із законом: r(t) = 7i + 4tj + 3t2k (м). За яким законом змінюється вектор швидкості V та вектор прискорення а частки? Знайти модуль вектора швидкості V в момент часу t = 3 с та переміщення тіла Δr за перші 4 с руху.задача 23063
Модуль швидкості v частки змінюється з часом t згідно із законом v = b + ct, де b і с - Позитивні постійні. Модуль прискорення а = 3 м/с2. Знайти тангенціальне aτ і нормальне аn прискорення частки.задача 23420
Рух матеріальної точки задано рівнянням r(t) = i(A + Bt2)+ jCt, де A = 10 м, В = –5 м/с2, С = 10 м/с; t — час. Для моменту часу t = 1 с обчислити модулі тангенційного та нормального прискорень.задача 23548
Знайти модулі швидкості та повного прискорення матеріальної точки в момент часу t1 = 2 c, якщо вона рухається згідно із законом: r = At·ex + B·sin ωt·ey; А = 8 м/с, В = –8 м, ω = π/2 рад/с.задача 23610
М'яч кинутий горизонтально зі швидкістю v0 = 9,8 м/с. Через який проміжок часу і в якому місці нормальне прискорення м'яча буде вдвічі більшим за тангенціальний?задача 23836
Тіло рухається по колу радіуса R = 2 м так, що кут повороту φ залежить від часу відповідно до рівняння φ(t) = A+Bt+Ct2+Dt3, де A = 0,1 рад, B = 0 рад/с, C = 0 рад/с2, D = 0,001 рад/с3. Для моменту часу t = 6 с визначте: а) кут повороту, пройдений шлях s і переміщення |Δr|; б) кутову та лінійну швидкості; в) кутове, тангенціальне, нормальне та повне прискорення.задача 23976
За час Δt = 0,4 с швидкість тіла змінилася від V1 = 14 м/с до V2 = 20 м/с та вектор швидкості повернувся на кут α = 5°. Визначити середні значення повного, нормального та тангенціального прискорення за цей проміжок часу. Завдання вирішити графічно. Графічну побудову виконати в масштабі: 1 см - 2 м/с. Розрахувати радіус кривизни траєкторії.задача 23990
Камінь кинутий з вежі в горизонтальному напрямку з початковою швидкістю v0 = 30 м/с. Визначити нормальне an прискорення каменю наприкінці четвертої секунди після початку руху.задача 24007
Точка рухається по колу радіусом 1 м із постійним тангенціальним прискоренням, рівним 73 см/с2. Через скільки часу після початку руху нормальне прискорення точки вдвічі більше за тангенційне?задача 24135
Тіло кинуто зі швидкістю v1 = 10 м/с під кутом α1 = 60° до горизонту. Знайдіть радіус кривизни траєкторії цього тіла, а також тангенціальне та нормальне прискорення в той момент, коли його швидкість складає з горизонтом кут α2 = 30°.задача 24163
Крапка рухається в площині так, що проекції її швидкості на осі прямокутної системи координат дорівнюють vx = 6π·cos(2π·t), vy = 6π·sin(2π·t). Обчисліть величину тангенціального прискорення точки, що відповідає моменту часу t = 1/π після старту.задача 24350
Точка рухається по кривій так, що її координати на площині описуються рівняннями: X = A1 + B1t + С1t3, Y = А2 + B2t + С2t2, где A1 = 3 м, B1 = 0,5 м/с, C1 = 0,1 м/с2, A2 = 2 м, B2 = 0,3 м/с, C2 = 0,8 м/с2. Знайдіть швидкість, повне, нормальне та тангенційне прискорення точки в момент часу t = 2 с. Побудуйте наступні залежності: v(t), an(t), aτ(t), a(t).задача 24484
Матеріальна точка рухається по колу радіусом r = 2 м відповідно до рівняння j = at+bt3, де a = 8 рад/с, b = -0,2 рад/с3. Знайти тангенціальне, нормальне та повне прискорення у момент часу t = 3 с.задача 24546
Крапка рухається по колу радіусом 20 см з постійним дотичним прискоренням 0,5 м/с2. Через скільки часу після початку руху нормальне прискорення точки дорівнюватиме тангенційному прискоренню?задача 24689
Матеріальна точка масою 1 г рухається по колу радіуса 2 м відповідно до рівняння S = 8t – 0,2t3. Знайти кутову та лінійну швидкість точки, тангенціальне, нормальне та повне прискорення точки в момент часу t = 2 с.задача 24875
Визначте, чому дорівнює повне прискорення а, а також його нормальна an та тангенціальна aτ складові та радіус кривизни R у вищій точці підйому тіла, кинутого під кутом α до горизонту з початковою швидкістю v0·задача 25016
Тіло рухається по колу радіусу R = 0,9 м так, що кут повороту φ залежить від часу відповідно до рівняння φ(t) = A+Bt+Ct2+Dt3, де A = 0,2 рад, B = 0,01 рад/с, C = 0,01 рад/с2, D = 0 рад/с3. Для моменту часу t = 4 с визначте:а) Кут повороту φ, пройдений шлях s та переміщення |Δr|;
б) кутову та лінійну швидкості;
в) кутове, тангенціальне, нормальне та повне прискорення.
задача 25017
Тіло рухається по колу радіусу R = 3 м так, що кут повороту φ залежить від часу відповідно до рівняння φ(t)=A+Bt+Ct2+Dt3, де A = 0,2 рад, B = 0 рад/с, C = 0,01 рад/с2, D = 0 рад/с3. Для моменту часу t = 8 с визначте:а) Кут повороту φ, пройдений шлях s та переміщення Δr.
б) Кутову та лінійну швидкості.
Кутове, тангенціальне, нормальне та повне прискорення.
задача 25018
Тіло рухається по колу радіусу R = 0,4 м так, що кут повороту φ залежить від часу відповідно до рівняння φ(t)=A+Bt+Ct2+Dt3, де A = 0 рад, B = –0,2 рад/с, C = 0,01 рад/с2, D = 0 рад/с3. Для моменту часу t = 4 с визначте:а) Кут повороту φ, пройдений шлях s та переміщення Δr.
б) Кутову та лінійну швидкості.
Кутове, тангенціальне, нормальне та повне прискорення.
задача 25020
Тіло рухається по колу радіусу R = 1 м так, що кут повороту φ залежить від часу відповідно до рівняння φ(t) = A+Bt+Ct2+Dt3, де A = 0 рад, B = 0,1 рад/с, C = 0,02 рад/с2, D = 0 рад/с3. Для моменту часу t = 10 с визначте:а) Кут повороту φ, пройдений шлях s та переміщення |Δr|;
б) кутову та лінійну швидкості;
в) кутове, тангенціальне, нормальне та повне прискорення.
задача 25021
Тіло рухається по колу радіусу R = 2 м так, що кут повороту φ залежить від часу відповідно до рівняння φ(t) = A+Bt+Ct2+Dt3, де A = 1 рад, B = 0 рад/с, C = 0 рад/с2, D = 0,002 рад/с3. Для моменту часу t = 10 с визначте:а) Кут повороту φ, пройдений шлях s та переміщення |Δr|;
б) кутову та лінійну швидкості;
в) кутове, тангенціальне, нормальне та повне прискорення.
задача 26047
Тіло, що спочатку покоїлось, пройшло за час t = 10 с півтора кола радіуса R = 5 м з постійним тангенційним прискоренням. Обчислити відповідні цьому проміжку часу значення: а) середнього модуля швидкості <v>, б) модуля середньої швидкості |<v>|, в) модуля середнього прискорення |<a>|.задача 26336
Тангенціальне прискорення матеріальної точки, що рухається по криволінійній траєкторії, змінюється за законом ατ = AS, де А = 5,00 1/с2, S - пройдений шлях. Маса точки дорівнює т = 5,00 кг. Чому дорівнює робота сил, що діють на матеріальну точку на ділянці траєкторії ΔS = 5,00 м?задача 26684
Однорідний диск, що має вагу Р = 124 Н, обертається з постійним кутовим прискоренням, і його рух описується рівнянням φ = 30t2+ 2t + 1. Диск обертається під дією постійної тангенціальної сили Fτ = 90 Н, прикладеної до обода диска. Визначити момент сил тертя, що діють на диск при його обертанні. Радіус диска R = 15 см.задача 26687
Колесо радіусом 0,3 м обертається згідно з рівнянням φ = 5-2t + 0,3t2. Знайти нормальне, тангенціальне і повне прискорення точок на ободі колеса через 5 с після початку руху.задача 26707
Закон руху матеріальної точки по колу радіусом 2м виражається рівнянням: S = 12-3t2. Знайти: 1) в який момент часу нормальне прискорення точки дорівнюватиме 36 м/с2; 2) чому дорівнюють швидкість, тангенціальне і повне прискорення точки в цей момент часу.задача 40000
Колесо з радіусом 0,1 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = 5+t+2t2+t3 рад. Для точок, що лежать на ободі колеса, визначити кутову швидкість, кутове, нормальне, тангенціальне і повне прискорення до кінця другої секунди. Який кут утворює вектор повного прискорення і вектор лінійної швидкості?задача 40124
Точка рухається по колу радіусом 4 м. Закон її руху виражається рівнянням s = 8 – 2t2, м. Визначити: а) в який момент часу нормальне прискорення точки дорівнюватиме 9 м/с2; б) чому дорівнюють швидкість, тангенціальне і повне прискорення точки в цей момент часу?задача 40485
Точка рухається по колу радіусом R = 4 м так, що в кожен момент часу її нормальне і тангенціальне прискорення рівні за модулем. B початковий момент часу t = 0 швидкість точки V0 = 0,2 м/с. Знайти швидкість точки в момент часу t1 = 10 c.задача 40503
За проміжок часу τ = 10,0 с частинка пройшла половину кола радіусом R = 160 см з постійним тангенціальним прискоренням. Обчислити за цей час а) середній модуль швидкості |< >|; б) модуль среднего вектора полного ускорения |<
>|; б) модуль среднего вектора полного ускорения |< >|.
>|.
задача 40541
Точка рухається по колу радіусом 8 м з постійним тангенціальним прискоренням, рівним 57 см/с2. Через скільки часу після початку руху нормальне прискорення точки буде вдвічі більше тангенціального?задача 40559
Точка рухається по колу радіусом R = 8 м. B деякий момент часу нормальне прискорення точки дорівнює 4 м/с2, вектор повного прискорення утворює в цей момент з вектором нормального прискорення кут 60°. Знайти лінійну швидкість і тангенціальне прискорення точки.задача 40639
Матеріальна точка рухається по колу радіуса 1 м згідно рівняння s = 8t – 0,2t3. Знайти швидкість, тангенціальне, нормальне і повне прискорення в момент часу 3 с.задача 40658
Точка обертається по колу радіусом R = 1,2 м. Рівняння руху точки φ = Аt + Вt3, де А = 0,5 рад/с; В = 0,2 рад/с3. Визначити тангенціальне аτ, нормальне an і повне а прискорення точки в момент часу t = 4 с.задача 40702
Колесо радіусом R = 0,1 м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = A+Bt+Ct2, де B = 2 рад/с, C = 1 рад/с2. Для точок, що лежать на ободі колеса, знайти через час t = 2с після початку руху: а) кутову швидкість ω; б) лінійну швидкість v; в) кутове прискорення ε; г) тангенціальне прискорення aτ; д) нормальне прискорення an.задача 40804
Матеріальна точка починає рухатися без початкової швидкості по колу радіусом R = 20 см з постійним тангенціальним прискоренням aτ = 5 см/с2. Через яке число обертів після початку руху нормальне прискорення точки стане рівним тангенціальному?задача 40841
Нормальна складова прискорення частинки, що рухається по колу радіусом R = 3,2 м, з плином часу за законом аn = Аt2, де А = 2,5 м/с2. Знайти: 1) шлях, пройдений частинкою за t1 = 5 с з моменту початку руху; 2) тангенціальну складову і повне прискорення в кінці цієї ділянки шляху.задача 40879
Камінь кинули під кутом 60° до горизонту зі швидкістю 12 м/с. Визначити нормальне і тангенціальне прискорення каменя через 0,5 с після початку руху. Через скільки часу, після початку руху нормальне прискорення каменя буде максимальним?задача 70318
Перпендикулярно однорідному магнітному полю (В = 1 мТл) збуджено однорідне електричне поле (E = 1 кВ/м). Перпендикулярно полям влітає α-частка зі швидкістю v = 1 Мм/с. Визначити нормальне аn і тангенціальне аτ прискорення α-частинки в момент входження її в поле.Другие предметы