обертається навколо осі з кутовою швидкістю радіус визначити масу
задача 10053
Платформа у вигляді диска діаметром D = 3 м і масою m1 = 180 кг може обертатися навколо вертикальної осі. З якою кутовою швидкістю буде обертатися ця платформа, якщо по її краю піде людина масою m2 = 70 кг зі швидкістю v = 1,8 м/с відносно платформи?задача 10057
На краю платформи у вигляді диска, що обертається за інерцією навколо вертикальної осі з частотою n1 = 8 хв–1, стоїть людина масою m1 = 70 кг. Коли людина перейшла в центр платформи, вона стала обертатися з частотою n2 = 10 хв–1. Визначити масу m2 платформи. Момент інерції людини розраховувати як для матеріальної точки.задача 10059
Горизонтальна платформа масою m1 = 150 кг обертається навколо вертикальної осі, що проходить чepeз центр платформи, з частотою n = 8 хв–1. Людина масою m2 = 70 кг варто при цьому на краю платформи. З якою кутовою швидкістю ω почне обертатися платформа, якщо людина перейде від краю платформи до її центру? Вважати платформу круглим, однорідним диском, a людину — матеріальною точкою.задача 10553
Платформа у вигляді диска радіусом R = l м обертається за інерцією з частотою n1 = 6 об/хв. На краю платформи стоїть людина, маса якої m = 80 кг. З якою частотою буде обертатися платформа, якщо людина перейде в її центр? Момент інерції платформи J = 120 кг·м2. Момент інерції людини розраховувати, як для матеріальної точки.задача 11029
Лінійна швидкість v1 точок на колі обертового диска дорівнює 3 м / с. Точки, розташовані на ΔR = 10 см ближче до осі, мають лінійну швидкість v2 = 2 м/с. Визначити частоту обертання n диска.задача 11037
Диск обертається з кутовим прискоренням ε = –2 рад/с2. Скільки обертів N зробить диск при зміні частоти обертання від n1 = 240 хв–1 до n2 = 90 хв–1? Знайти час Δt, протягом якого це станеться.задача 11087
По площині диска радіуса R = 10 см рівномірно розподілений заряд з поверхневою площиною σ = 0,5 нКл/см2. Диск рівномірно обертається з частотою n = 1,8·103 об/хв навколо осі, що проходить через центр диска перпендикулярно його площині. Визначити магнітний момент рт, створюваний обертовим диском.задача 11159
Куля масою m = 10 кг і радіусом R = 20 см обертається навколо осі, що проходить через його центр. Рівняння обертання кулі має вигляд φ = A+Bt2+Ct3, де В = 4 рад/с2, С = –1 рад/с3. Знайти закон зміни моменту сил, що діють на кулю. Визначити момент сил М в момент часу t = 2 с.задача 11178
Куля масою m = 10 г летить зі швидкістю v = 800 м/с, обертаючись близько поздовжньої осі з частотою n = 3000 с–1. Беручи кулю за циліндрик діаметром d = 8 мм, визначити повну кінетичну енергію Т кулі.задача 11371
Стрижень масою 3 кг і довжиною 1.5 м обертається навколо осі, що проходить через один з його кінців, за законом φ = 6+4t+2t2. Визначити момент сили, що діє на інший його кінець.задача 11410
Візок рухається зі швидкістю v. На ньому обертається диск з кутовою швидкістю ω. Радіус ротора дорівнює r. Визначити абсолютні швидкості трьох точок ротора, зазначених на малюнку.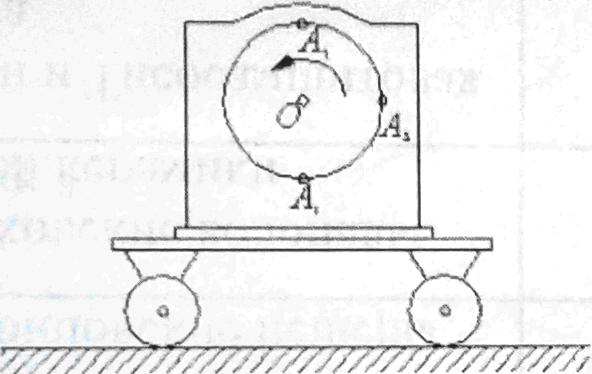
задача 11875
Диск обертається навколо осі, що проходить через його центр мас. Залежність кута повороту від часу має вигляд φ(t) = –4 + 2π(t + t2) (рад). Для моменту часу t1 = 2 с знайти: 1) скільки оборотів зробить диск; 2) кутову швидкість; 3) кутове прискорення. Визначити для точки, що знаходиться на відстані r = 0,1 м від осі обертання, повне лінійне прискорення в момент часу t2, коли диск зробив N = 2 оберти.задача 12620
Горизонтальна платформа, що має форму диска, обертається навколо вертикальної осі, роблячи 10 об/хв. На краю платформи стоїть людина, маса якої 60 кг. Визначити частоту обертання, якщо людина перейде у центр платформи. Маса платформи 250 кг, її радіус 3,5 м. Людину вважати точковою масою.задача 12715
Платформа, що має форму диска, обертається близько вертикальної осі з частотою n1 = 10 мин–1. На краю платформи стоїть людина. З якою частотою n2 обертатиметься платформа, якщо людина перейде до її центру? Маса платформи m1 = 280 кг, маса людини m2 = 80 кг. Платформу вважати круглим однорідним диском, а людину – точковою масою.задача 13027
Колесо обертається з постійним кутовим прискоренням ε = 3 рад/с. Визначте радіус колеса, якщо через t = 1 с після початку руху повне прискорення колеса а = 7,5 м/с2.задача 13133
Куля радіусом R = 10 см і масою m = 5 кг обертається навколо осі симетрії згідно рівняння φ = А + Вt² + Сt³ (В = 2 рад/с², С = −0,5 рад/с³). Визначте момент сил М для t = 3 с.задача 13153
Людина масою m = 60 кг, стоїть на краю горизонтальної платформи масою М = 120 кг, обертається за інерцією навколо нерухомої вертикальної осі з частотою n1 = 10 хв−1, переходить до її центру. Вважаючи платформу круглим однорідним диском, a людину - точковою масою, визначте, з якою частотою n2 буде тоді обертатися платформа.задача 13171
Дві матеріальні точки масами m1 і m2 розташовані один від одного на відстані R. Визначте кутову швидкість обертання, з якою вони повинні обертатися навколо загального центру мас, щоб відстань між ними залишилася постійною.задача 13447
Диск маси m і радіуса R рівномірно обертається навколо своєї осі з кутовою швидкістю ω. Під дією зовнішніх сил диск зупиняється. Чому дорівнює робота А зовнішніх сил?задача 13828
Диск масою 2 кг і радіусом 0,1 м обертається навколо осі, що проходить через його центр. Рівняння руху φ = 5 – 6t 2 + t3. Визначити момент сил, що діють на диск, в момент часу 4 с. Визначити закон зміни моменту сил.задача 13829
Куля масою 10 кг і радіусом 20 см обертається навколо осі, що проходить через її центр. Рівняння обертання кулі має вигляд: φ = 2+4t2–t3. Знайти закон зміни моменту сил, що діють на кулю. Визначити момент сил в момент часу 2 с.задача 13840
Горизонтальна платформа масою 250 кг обертається навколо вертикальної осі, роблячи 10 об/хв. На краю платформи стоїть людина — точкова маса 80 кг. У скільки разів збільшиться кінетична енергія платформи, якщо людина переміститься на 0,5R до центру платформи? (R — радіус платформи).задача 14238
Однорідний диск може вільно обертатися навколо горизонтальної осі, що проходить через його центр О. В точку А на твірній диска потрапляє горизонтально летюча маленька пластилінова кулька і прилипає до його поверхні. Швидкість v кульки дорівнює 10 м/с. Визначити лінійну швидкість u точки В на диску в початковий момент часу. Маса m1 кульки дорівнює 10 г. Маса m2 диска дорівнює 0,1 кг.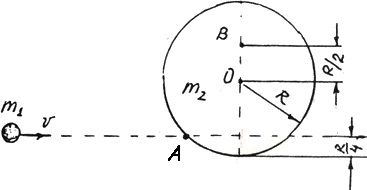
задача 14451
Вал обертається з частотою n = 180 об/хв. З деякого моменту вал починає обертатися рівноуповільнено з кутовим прискоренням ε = 3 рад/с2. Через який час t вал зупиниться? Знайти число обертів N валу до зупинки.задача 14460
Колесо обертається з кутовим прискоренням ε = 2 рад/с2. Через час t = 0,5 с після початку руху повне прискорення колеса а = 13,6 см/с2. Знайти радіус R колеса.задача 14539
Металевий диск радіуса R обертається з кутовою швидкістю ω навколо осі, перпендикулярної до диску і що проходить через її центр. Знайти величину вектора напруженості електричного поля, що виник на краю диска.задача 14640
Дві гирі з різними масами з'єднані ниткою, перекинутою через блок, момент інерції якого J = 50кг·м2 і радіус R = 20 см. Момент сил тертя обертового блоку Mтр = 98,1 Н·м. Знайти різницю сил натягу нитки T1–Т2 по обидві сторони блоку, якщо відомо, що блок обертається з кутовим прискоренням ε = 2,36 рад/с2. Блок вважати однорідним диском.задача 14666
Горизонтальна платформа масою m = 100 кг обертається навколо вертикальної осі, що проходить через центр платформи, з частотою n1 = 10 об/хв. Людина масою m0 = 60 кг варто при цьому на краю платформи. З якою частотою n2 почне обертатися платформа, якщо людина перейде від краю платформи до її центру? Вважати платформу однорідним диском, а людину — точковою масою.задача 14670
Людина масою m0 = 60 кг знаходиться на нерухомій платформі масою m = 100 кг. З якою частотою n буде обертатися платформа, якщо людина буде рухатися по колу радіусом r = 5 м навколо осі обертання? Швидкість руху людини щодо платформи v0 = 4 км/год. Радіус платформи R = 10 м. Вважати платформу однорідним диском, людини - точковою масою.Задача 23952
Молекулу NO2 можна змоделювати трикутником, у вершинах якого знаходяться ядра атомів. Кут між ядрами кисню дорівнює 140°. Відстань між ядрами азоту і кисню одно 0,118 нм. Визначте радіус кола, описуваного ядром азоту, вважаючи, що молекула обертається навколо осі, перпендикулярної її площині і що проходить через центр мас.Задача 24042
Два горизонтальних диска вільно обертаються в різних напрямках навколо вертикальної осі, що проходить через їх центри. Маси дисків рівні 10 кг і 40 кг, їх радіуси 0,2 м і 0,1 м, кутові швидкості 10 рад/с і 20 рад/с відповідно. Після падіння верхнього диска на нижній обидва диска завдяки тертю між ними почали через деякий час обертатися як єдине ціле. Знайдіть зміну сумарної кінетичної енергії дисків.задача 14690
Тіло обертається так, що залежність кутової швидкості від часу визначається рівнянням; ω = 2 + 0,5t. Знайти повне число обертів, здійснених тілом за 20 с після початку обертання. Вказати початкову кутову швидкість і прискорення тіла.задача 15000
На краю каруселі, що має форму диска, масою 200 кг і діаметром 4 м, що обертається з частотою 1 об/с, стоять п'ять чоловік, кожен масою по 60 кг. Знайти частоту обертання каруселі, якщо всі люди змістяться до її центру на половину радіуса. Вважати, що в порівнянні з розміром каруселі люди являють собою матеріальні точки.задача 15026
Візки пов'язані ниткою і обертаються, не зміщуючись, на відцентровій машині. Визначте масу другого візка, якщо r1 = 30 см; r2 = 10 см, а маса першого візка дорівнює 300 г.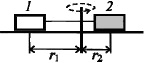
задача 15037
Людина масою 80 кг знаходиться на нерухомій круглій платформі радіусом 20 м і масою 200 кг, яка може обертатися навколо своєї вертикальної осі. З якою кутовою швидкістю буде обертатися платформа, якщо людина буде рухатися по колу радіусом 10 м з лінійною швидкістю 2,5 м/с щодо платформи?задача 15453
Людина масою m знаходиться на нерухомій круглій платформі масою M і радіусом R, яка може обертатися навколо вертикальної осі симетрії платформи. З якою кутовою швидкістю буде обертатися платформа, якщо людина почне рухатися по колу радіусом r зі швидкістю v відносно платформи?задача 15613
Яку мінімальну швидкість V повинен мати математичний маятник, проходячи через положення стійкої рівноваги, для того щоб він міг обертатися по колу у вертикальній площині?задача 15888
Визначте період обертання навколо Землі супутника, який віддалений від поверхні Землі на відстань, рівну трьом радіусам Землі.задача 16064
Куля масою 10 кг і радіусом 20 см обертається навколо осі, що проходить через її центр. Залежність кута повороту кулі від часу має вигляд: φ = Сt2, де С = 10 рад/с2. Визначити момент сил, що діють на кулю.задача 16598
Обруч радіусом R, який обертається навколо вертикальної осі, перпендикулярної до площини обруча і проходить через його центр, з кутовою швидкістю ω0, опускають на горизонтальну поверхню. Коефіцієнт тертя обруча об поверхнюзадача 16714
Колесо обертається навколо нерухомої осі з кутовим прискоренням ε = At2 + В, де А = 12 рад/с4, В = 4 рад/с2. На який кут повернеться колесо через 2 с, якщо в початковий момент часу кутова швидкість ω0 = 0 і кут повороту φ0 = 0.задача 18193
Стрічка перемотується з однієї котушки на іншу. Швидкість подачі стрічки постійна і дорівнює ν. Знайти кутову швидкість обертання мотка через час t після початку перемотування. Початковий радіус мотка r0, товщина стрічки Δl.задача 18269
Платформа, що представляє собою однорідний суцільний циліндр масою 200 кг і радіусом 2 м, на краю якої стоїть людина масою 80 кг, обертається без тертя навколо вертикальної осі з частотою 18 об/хв. Людина почала рухатися по краю платформи зі швидкістю 2 м/с щодо неї в напрямку її обертання? З якою частотою стала обертатися платформа. Людину розглядати як матеріальну точку.задача 19581
Супутник обертається навколо Землі в площині екватора. Визначте висоту орбіти h, якщо за добу супутник здійснює n = 14 обертів навколо Землі.задача 19670
Однорідний тонкий стрижень, що знаходиться на гладкій горизонтальній поверхні, вільно обертається навколо свого кінця з деякою кутовою швидкістю ω0. В деякий момент вісь витягують, і стрижень ковзає по площині, обертаючись. Визначити кутову швидкість цього обертання.задача 19689
На малюнку дано графік залежності енергії тіла, що обертається Wвр від кутової швидкості. Чому буде дорівнювати момент імпульсу тіла, при величині кутової швидкості рівній ω = 4 рад/с?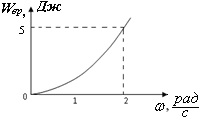
задача 19853
На однорідний суцільний циліндр радіуса r = 0,2 м і маси m = 1 кг, який може обертатися навколо осі, що збігається з його віссю симетрії (вісь z), намотана нитка. За нитку тягнуть так, що залежність кута повороту циліндра від часу має вигляд φ(t) = Bt3, де B = 10 рад·с–3. Визначити силу натягу нитки через дві секунди після початку обертання циліндра, якщо з боку осі на циліндр, що обертається діє постійний гальмуючий момент, величина якого |Mтр| = 1 Н·м.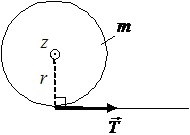
задача 19854
Однорідна кулю радіуса r = 0,1 м і маси m = 2 кг може обертатися навколо осі z, що проходить через її центр. На "екватор" кулі намотана нитка, за яку тягнуть так, що залежність кута повороту кулі від часу має вигляд φ(t) = Bt4, де B = 1 рад·с–4. Визначити силу натягу нитки через дві секунди після початку обертання кулі, якщо з боку осі на кулю, що обертається, діє постійний гальмуючий момент, величина якого |Mтр| = 10 Н·м.
задача 19863
Однорідний суцільний циліндр радіусом r = 0,5 м і масою m = 2 кг може обертатися навколо горизонтальної осі (точка О). Його відхилили з положення рівноваги на кут 90° і відпустили. Визначити постійний момент сили тертя, який вісь прикладає до циліндра, якщо при проходженні положення рівноваги кутова швидкість циліндра ω = 5 рад/с.
задача 19908
На малюнку дано графік залежності моменту імпульсу кулі, що обертається навколо осі, яка проходить через його центр, від часу. 1) Побудувати графік залежності моменту сили, що діє на кулю, від часу. 2) Визначити величину кутової швидкості і кутового прискорення кулі при t = 2 с. Маса кулі 1 кг, радіус кулі 50 см.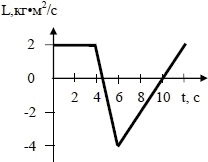
задача 19917
Диск радіусом 10 см і масою 2 кг обертається навколо осі, що проходить перпендикулярно його площині через середину радіуса. Закон руху диска φ = 6 + 4t – t2 (рад). Визначити момент сили, що діє на диск, і кінетичну енергію диска через 2 с після початку обертання диска. Побудувати графік залежності моменту сили і моменту імпульсу диска від часу.задача 20144
Людина масою 70 кг, що стоїть на краю платформи радіусом 2 м і масою 100 кг, кидає по дотичній до краю вантаж масою 2 кг зі швидкістю 4 м/с. З якою кутовою швидкістю почне обертатися платформа?задача 20370
На малюнку показані тіла однакової маси і розмірів, що обертаються навколо вертикальної осі з однаковою частотою. Кінетична енергія першого тіла Wк1вр = 0,5 Дж. Знайдіть момент імпульсу другого тіла, якщо m = 1 кг, R = 10 см.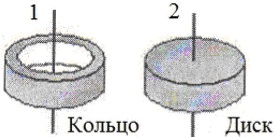
задача 20406
Тонкий диск з постійною щільністю заряду обертається навколо осі, що проходить через центр перпендикулярно площині диска. Радіус диска а, заряд Q, кутова швидкість обертання ω. Знайдіть індукцію магнітного поля в центрі диска.задача 20455
Суцільний диск масою 0,2 кг обертається навколо осі, що проходить через його центр мас під дією моменту сил 0,8·10–2 Н·м. Закон обертання має вигляд φ = 5–t+2t2. Визначити радіус диска.задача 20744
Однорідний диск радіусом R = 20 см і масою m1 = 0,20 кг може вільно обертатися навколо нерухомої горизонтальної осі, перпендикулярної площині диска і що проходить через точку О на ньому. В точку А на твірній диска потрапляє пластилінова кулька, що летить горизонтально зі швидкістю v = 10 м/с, і прилипає до його поверхні. Маса кульки m2 = 10 г. Визначте кутову швидкість диска і лінійну швидкість точки В відразу після прилипання кульки (див. рис.).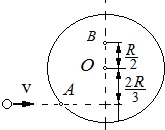
задача 20869
По сфері радіуса R = 10 см рівномірно розподілений заряд Q = 10–8 Кл. Сфера обертається з частотою f = 10 1 / c щодо осі, що проходить через центр сфери. Знайти магнітний момент кругового струму, створюваного сферою, що обертається.задача 21102
Горизонтальна платформа в формі диска (m1 = 100 кг; R = 1,5 м) обертається навколо своєї осі, здійснюючи 10 оборотів в хвилину. Людина (m2 = 60 кг) стоїть на краю платформи. Якою буде частота обертання, якщо людина перейде від краю платформи до центру?задача 21385
Тонкий стрижень масою m і довжиною l обертається з кутовою швидкістю 10 с–1 в горизонтальній площині навколо вертикальної осі, що проходить через середину стержня. Продовжуючи обертатися в тій же площині, стрижень переміщається так, що вісь обертання тепер проходить через кінець стержня. Знайти кутову швидкість у другому випадку.задача 21418
Платформа у вигляді суцільного диска радіусом 1,5 м і масою 180 кг обертається за інерцією навколо вертикальної осі з частотою ν = 10 хв–1. На краю платформи стоїть людина масою 60 кг. Яку кутову швидкість матиме платформа, якщо людина перейде в центр платформи?задача 21528
Однорідний суцільний циліндр, що має радіус r = 0,1 м і масу m = 1 кг, може обертатися навколо осі, що збігається з його віссю симетрії (вісь z). На циліндр намотана нитка, за яку тягнуть так, що залежність кута повороту циліндра від часу має вигляд φ(t) = Bt5, де B = 1 рад·с–5. Визначити момент часу, коли сила натягу нитки T стане рівною 28 Н, якщо з боку осі на циліндр, що обертається, діє постійний гальмуючий момент, величина якого |Mтр| = 2 Н·м.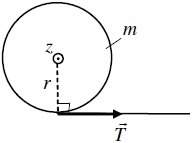
задача 21572
Людина масою 70 кг, що стоїть на краю горизонтальної платформи масою 1000 кг, що обертається навколо нерухомої вертикальної осі з кутовою швидкістю 0,2 рад/с, переходить до її центру. Вважаючи платформу однорідним диском, а людину - матеріальною точкою, визначте, з якою частотою буде обертатися платформа після цього переходу.задача 22406
Платформа у вигляді горизонтального диска масою М = 200 кг і радіусом R = 1 м обертається навколо вертикальної осі з частотою n = 6 об/хв. На краю платформи стоїть людина масою m = 75 кг. Людина ловить м'яч масою m0 = 1 кг, летить горизонтально зі швидкістю υ = 5 м/с на відстані, рівній радіусу платформи, від її центру. З якою кутовою швидкістю ω на відстані, рівній радіусу платформи, від її центру. З якою кутовою швидкістюзадача 22895
На малюнку стрілками показані напрями кутового прискорення дисків, що обертаються, а також вказано, як змінюється їх кутова швидкість по модулю з плином часу. Який із дисків обертається проти годинникової стрілки (якщо дивитися зверху)?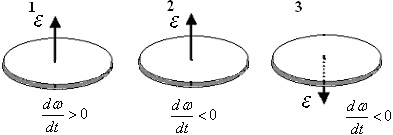
задача 22896
На малюнку стрілками показані напрями кутового прискорення дисків, що обертаються, а також вказано, як змінюється їх кутова швидкість по модулю з плином часу. Які диски обертаються проти годинникової стрілки (якщо дивитися зверху)?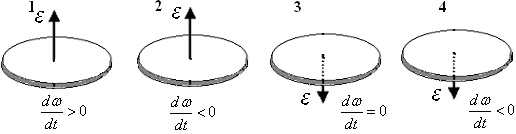
задача 23397
На малюнку дано графік залежності енергії тіла, що обертається Wвр від кутової швидкості. Чому дорівнюватиме момент імпульсу тіла, при величині кутової швидкості, рівної ω = 3 рад/с?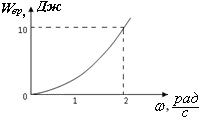
задача 23703
Тіло обертається навколо нерухомої осі згідно із законом φ = At – Bt2, де A = 10 рад/с, В = 2,0 рад/с2. Через який час тіло зупиниться і скільки обертів зробить до зупинки?задача 24008
Визначити середнє кутове прискорення маховика, кутова швидкість якого за час 18 повних обертів зросла від частоти 7 обертів на секунду до 17 обертів на секунду.задача 24046
Куля радіусом R = 0,20 м та масою m = 10 кг обертається навколо осі, що проходить через його центр. За яким законом змінюється момент сили та момент імпульсу кулі, якщо кутове прискорення кулі змінюється з часом за законом ε = A·t, c–2, де А = 2 с–3. У початковий момент часу (t = 0) куля була нерухома.задача 24518
Однорідний стрижень завдовжки l = 1,2 м і масою m = 0,3 кг обертається в горизонтальній площині навколо вертикальної осі, що проходить через один із його кінців з кутовим прискоренням ε = 9,81 с–1. Скільки оборотів зробить стрижень за час t = 5,0 с, якщо він почав обертатися зі стану спокою? Як зміниться момент, що обертає, якщо вісь обертання перемістити в центр мас стрижня, а діюча сила не змінюється?задача 24531
Сфера радіусом R = 2,0 м рівномірно обертається навколо вертикального діаметра із частотою n = 60 об/хв. Усередині сфери знаходиться кулька масою m = 0,3 кг. Знайти висоту h, відповідну положенню рівноваги кульки щодо дна сфери, та реакцію сфери N.задача 24586
Людина масою 80 кг стоїть на краю нерухомої платформи, що є однорідним суцільним циліндром масою 100 кг і радіусом 2 м, який може обертатися без тертя навколо вертикальної осі. З якою кутовою швидкістю почне обертатися платформа після того, як людина зловить м'яч масою 0,5 кг, що летить горизонтально по дотичній до платформи зі швидкістю 10 м/с. Людину розглядати як матеріальну точку.задача 24587
Внаслідок вибуху зірка, яка оберталася навколо своєї осі, збільшила об'єм у 8 разів. Вважаючи зірку однорідною кулею, визначити яким став період її обертання, якщо до вибуху він дорівнював 1 місяцю?задача 24609
Нормальне прискорення точки М диска, що обертається навколо нерухомої осі, дорівнює 6,4 м/с2. Визначити кутову швидкість ω цього диска, якщо його радіус R = 0,4 м.задача 24720
На графіку представлена залежність кута φ повороту тіла, що обертається від часу t. Визначте початкову кутову швидкість обертання тіла.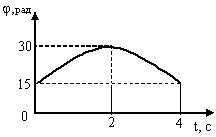
задача 24721
Тіло обертається навколо нерухливої осі. Залежність кутової швидкості від часу ω(t) показано на рисунку. Напишіть рівняння φ = f(t), відбиває залежність кута повороту тіла від часу, якщо початкове положення тіла відповідає значенню φ0 = 2 рад.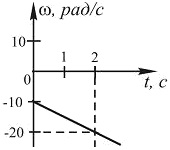
задача 24754
Платформа у вигляді диска діаметром D = 4 м та масою m1 = 200 кг обертається навколо вертикальної осі. З якою кутовою швидкістю ω1 буде обертатися ця платформа, якщо її краєм пройде людина масою m2 = 65 кг із швидкістю v = 1,5 м/с щодо платформи?задача 24962
Суцільний металевий циліндр радіуса R обертається з постійною кутовою швидкістю ω. Знайдіть залежність напруженості поля Е від відстані r від осі циліндра та різниця потенціалів U між поверхнею циліндра та його віссю.задача 24970
Однорідний диск радіуса 0,2 м та маси 5 кг обертається навколо осі, що проходить через його центр. Залежність кутової швидкості обертання диска іноді дається рівнянням ω(t) = 0,5 + 8t, рад/с. Знайти величину дотичної сили, що утворює момент, що крутить.задача 24991
Між зубчастими колесами радіусами R та r знаходиться в зачепленні ролик (рис. 1.14). Колеса починають обертатись у протилежні сторони з кутовими швидкостями ω1 і ω2. Якою буде кутова швидкість обертання ролика навколо власної осі? Куди і з якою швидкістю рухатиметься вісь ролика? Розв'яжіть задачу за умови, що колеса обертаються в один бік.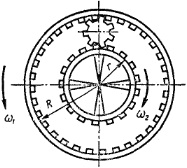
задача 25040
Однорідний диск радіусу R = 80 см може обертатися у вертикальній площині навколо горизонтальної осі, що проходить через точку O на ньому, віддалену на відстань a = R/2 від центру диска. Диск відхилено від положення рівноваги на кут α = 30° і відпустили. Визначте: а) початкові кутове прискорення диска ε та тангенціальне прискорення aτс його центру мас, б) кутову ω та лінійну швидкості vc центру мас диска під час проходження ним положення рівноваги.задача 25041
Однорідний диск радіусу R = 40 см може обертатися у вертикальній площині навколо горизонтальної осі, що проходить через точку O на ньому, віддалену на відстань a = R/4 від центру диска. Диск відхилено від положення рівноваги на кут α = 50° і відпустили. Визначте: а) початкові кутове прискорення диска ε та тангенціальне прискорення aτс його центру мас, б) кутову ω та лінійну швидкості vc центру мас диска під час проходження ним положення рівноваги.задача 25042
Однорідний диск радіусу R = 40 см може обертатися у вертикальній площині навколо горизонтальної осі, що проходить через точку O на ньому, віддалену на відстань a = R/2 від центру диска. Диск відхилено від положення рівноваги на кут α = 25° і відпустили. Визначте: а) початкові кутове прискорення диска ε та тангенціальне прискорення aτс його центру мас, б) кутову ω та лінійну швидкості vc центру мас диска під час проходження ним положення рівноваги.задача 25179
Однорідний диск радіуса R = 100 см може обертатися у вертикальній площині навколо горизонтальної осі, що проходить через точку О на ньому, що віддаляється на відстань a = R від центру диска. Диск відхилили від рівноваги на кут α = 20° і відпустили. Визначте: а) початкове кутове прискорення диска ε та тангенціальне прискорення aτс його центру мас, б) кутову ω та лінійну швидкості vc центру мас диска під час проходження ним положення рівноваги.задача 25961
Горизонтальна платформа масою 100 кг обертається навколо вертикальної осі, що проходить через центр платформи, роблячи 10 об/хв. Людина вагою 60 кг стоїть при цьому на краю платформи. З якою швидкістю почне обертатися платформа, якщо людина перейде до її центру? Вважати платформу круглим однорідним диском, а людину — точковою масою.задача 26355
На краю круглої горизонтальної платформи радіусом R = 0,40 м стоїть людина. Платформа разом з ним обертається з кутовою швидкістю ω0 = 25,0 рад/с навколо вертикальної осі, що проходить через центр ваги платформи. У деякий момент часу людина починає йти вздовж краю платформи зі швидкістю vч = 1,80 м/с (по відношенню до платформи) в протилежну сторону її обертання. Знайти змінену швидкість платформи ωч, якщо її маса M = 200 кг, а маса людини m = 70,0 кг.задача 26401
Горизонтальна платформа масою m = 30 кг зі стоячою на її краю людиною обертається з частотою n1 = 5 об/хв навколо вертикальної осі, що проходить через її центр. З якою частотою почне обертатися платформа, якщо людина масою m1 = 60 кг перейде від краю платформи до її центру? Вважати людину матеріальною точкою, а платформу-однорідним диском.задача 26417
За наведеним графіком побудувати графіки залежності кутового прискорення і кутового шляху від часу, враховуючи, що φ(0) = 0. Визначити число обертів, зроблене обертовим тілом за перші 6 с руху.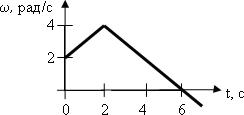
задача 26440
Обруч радіусом r = 0,5м і масою m = 1 кг може обертатися навколо горизонтальної осі (точка О). Його відхилили з положення рівноваги на кут 90 ° і відпустили. Визначити постійний момент сили тертя, який вісь прикладає до обруча, якщо при проходженні положення рівноваги кутова швидкість обруча ω = 4 рад/с.
задача 26490
Гирька лежить на обертовому щодо вертикальної осі диску. На якій відстані від осі лежить гирька, якщо диск обертається з кутовою швидкістю 10 рад/с? Коефіцієнт тертя між диском і гирькою дорівнює 0,1.Задача 26585
Котушка обертається навколо осі OO1 з кутовою швидкістю ω = 2 рад/с. Уздовж котушки переміщається точка М за законом М0М = 0,04t2. Визначити абсолютне прискорення точки M, якщо радіус r = 0,02 м.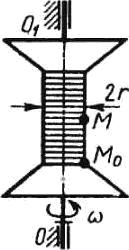
Задача 26586
По стороні трикутника, що обертається навколо боку АВ з постійною кутовою швидкістю ω = 4 рад/с, рухається точка М з відносною швидкістю vr. У момент часу, коли відстань МВ = 0,5 м, визначити модуль переносного прискорення точки M, якщо кут α = 30°.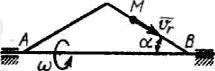
Задача 26599
Резервуар 1, момент інерції якого щодо вертикальної осі ?z дорівнює 1 кг·м2, обертається з кутовою швидкістю ω0 = 18 рад/с. Після відкриття засувки 2 він заповнюється сипучим матеріалом. Визначити кутову швидкість заповненого резервуара, якщо його момент інерції дорівнює 3 кг·м2.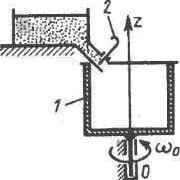
Задача 26602
До диску, який обертається навколо осі О, притискаються дві гальмівні колодки з силами F1 = F2 = 100 Н. Обчислити роботу сил тертя ковзання при гальмуванні диска радіуса r = 0 , 1 м за 10 обертів. Коефіцієнт тертя ковзання гальмівної колодки про диск f = 0,3.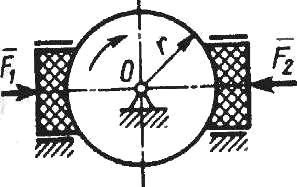
Задача 26615
Яку початкову кутову швидкість ω0 треба надати однорідному стрижню довжиною l = 3 м, щоб він, обертаючись навколо горизонтальної осі О, зробив півоберта?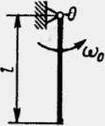
задача 26625
Визначити модуль постійного моменту М пари сил, при дії якої барабан I обертається з кутовим прискоренням ε = 1 рад/с2. Барабан 1 і каток 2 - однорідні циліндри однакового радіуса r = 0,2 м, маси тіл m1 = m2 = 2 кг.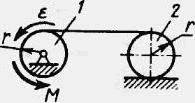
задача 26665
Платформа у вигляді диска радіусом R = 1 м обертається за інерцією з частотою n1 = 6 об/хв. На краю платформи стоїть людина, маса якої m = 88 кг. З якою частотою буде обертатися платформа, якщо людина перейде в її центр? Момент інерції платформи J = 120 кг·м2. Момент інерції людини розраховувати як для матеріальної точки.задача 26692
Куля масою 10 кг і радіусом 20 см обертається навколо осі, що проходить через його центр. Кут повороту змінюється в часі за законом φ = А + Вt2+ Сt3, де А = 5 рад; B = 4 рад/c2; C = -1 рад/c3. Визначити величину моменту сил, прикладених до кулі в момент часу 2 с.задача 26724
Однорідний диск радіуса R = 60 см може обертатися у вертикальній площині навколо горизонтальної осі, що проходить через точку О на ньому, яка віддалена на відстань a = R/3 від центру диска. Диск відхилили від положення рівноваги на кут. α = 40° і відпустили. Визначте: а) початкове кутове прискорення диска ε та тангенціальне прискорення aτс його центру мас, б) кутову ω та лінійну швидкості vc центру мас диска під час проходження ним положення рівноваги.задача 40490
На два взаємно перпендикулярних стрижня, що утворюють хрестовину, надіті чотири кулі масою 30 г і радіусом 2,5 см. Коли кулі знаходяться на відстані 10 см від осі обертання, що проходить через центр хрестовини, система обертається з частотою 3 об / с. C якою частотою стане обертатися дана система, якщо під час обертання кулі перемістяться на краї стрижнів. Довжина кожного стрижня 30 см, маса 150 г.задача 40496
На верхній поверхні горизонтального диска, який може обертатися навколо вертикальної осі, прокладені по колу радіусом 50 см рейки іграшкової залізниці. Маса диска 10 кг, його радіус 60 см. На рейки нерухомого диска був поставлений заводний паровозик масою 1 кг і випущений з рук. Він почав рухатися відносно рейок зі швидкістю 0,8 м/с. C якою кутовою швидкістю буде обертатися диск?задача 40521
Космонавт, маса якої m = 75 кг, знаходиться в центрифузі, що обертається навколо вертикальної осі з кутовою швидкістю ω = 4,33 рад/с. Радіус центрифуги R = 3 м. Визначити числове значення і напрям ваги Р космонавта.задача 40522
Куля, радіус якого R = 0,1 м і маса m = 10 кг, обертається навколо своєї осі згідно рівняння φ = Аt3 + Bt2 + С, де А = 1 рад/с3, В = –3 рад/с2. Визначити момент сили М для моментів часу t1 = 1 с і t2 = 2 с.задача 40741
Кутова швидкість обертового тіла змінюється за законом ω = 2t + 3t2. На який кут повернулося тіло зa час від t1 = 1 с до t2 = 3 с?задача 40811
Диск радіусом R обертається з кутовою швидкістю ω = 2 – 2t. Чому дорівнює кутове прискорення диска? Як спрямовані вектори кутової швидкості та кутового прискорення? Зробити креслення. Вісь обертання проходить через центр диска.задача 40813
Тіло обертається навколо нерухомої осі. Кутове прискорення ε = –3 с–2. Початкове значення кутової швидкості 30 с–1. Записати закон зміни кутової швидкості. Показати на малюнку, як спрямовані вектори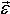 і
і 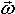 .
.
задача 40858
Шар радіусом 10 см і масою 5 кг обертається навколо вісі симетрії за законом φ = A + Bt2 + Ct3, де В = 2 рад/с2, С = –0,5 рад/с3. Визначити момент сил відносно вісі обертання для моменту часу t = 3 c.Другие предметы