кінематичний вісь прискорення точка визначити матеріал рівняння руху швидкість момент часу де
задача 10502
Рухи двох матеріальних точок виражаються рівняннями x1 = A1 + В1t + С1t2 і x2 = A2 + В2t + С2t2 де A1 = 20 м; В1 = 2 м/с; С1 = –4 м/с2; A2 = 2 м; B2 = 2 м/с; С2 = 0,5 м/с2. У який момент часу швидкості цих точок будуть однакові? Чому дорівнюють швидкості і прискорення точок в цей момент?задача 10988
Рух матеріальної точки задано рівнянням x = At+Bt2, де A = 4 м/с, В = -0,05 м/с2. Визначити момент часу, в який швидкість v точки дорівнює нулю. Знайти координату і прискорення в цей момент. Побудувати графіки залежності координати, шляху, швидкості і прискорення цього руху від часу.задача 10993
Рухи двох матеріальних точок виражаються рівняннями: x1 = A1+B1t+C1t2, x2 = A2+B2t+C2t2, де A1 = 20 м, A2 = 2 м, B1 = B2 = 2 м/с, C1 = -4 м/с2, С2 = 0,5 м/с2. У який момент часу t швидкості цих точок будуть однаковими? Визначити швидкості v1 і v2 і прискорення a1 і а2 точок в цей момент.задача 11015
Точка А рухається рівномірно зі швидкістю v по колу радіусом R. Початкове положення точки і напрямок руху вказані на малюнку. Написати кінематичне рівняння руху проекції точки A на напрям осі х.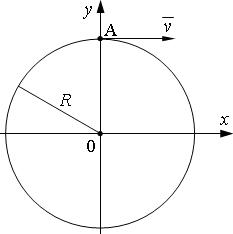
задача 11017
Написати для чотирьох випадків, представлених на малюнку: 1) кінематичні рівняння руху x = f1(t) і x = f2(t); 2) рівняння траєкторії у = φ(х). На кожній позиції малюнка - а, б, в, г - зображені координатні осі, вказані початкове положення точки A, її початкова швидкість v0 і прискорення g.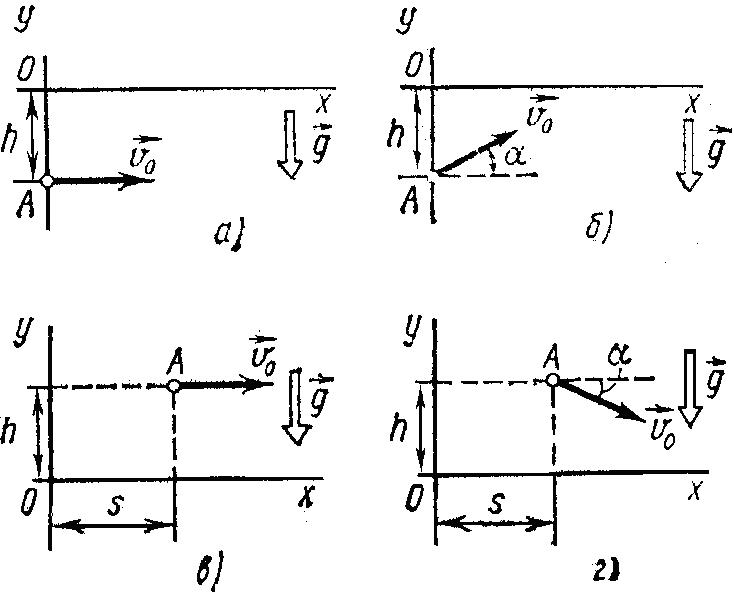
задача 12264
Кінематичні рівняння двох матеріальних точок мають вигляд x1 = A1t + B1t2 + C1t3 і x2 = A2t + B2t2 + C2t3, де B1 = 4 м/с2, C1 = –3 м/с, B2 = 4 м/с, C2 = 1 м/с3. Визначити момент часу, для якого прискорення цих точок будуть рівні.задача 13016
Кінематичні рівняння руху двох матеріальних точок мають вигляд х1 = A1t + B1t² + С1t³ і х2 = A2t + В2t² + C2t³, де В1 = 4 м/с², С1 = −3 м/с³, В1 = −2 м/с², С2 = 1 м/с³. Визначте момент часу, для якого прискорення цих точок будуть рівні.Задача 23961
У таблиці наведені рівняння зміни з часом кінематичних характеристик обертового маховика, закріпленого на валу двигуна. 1. Побудуйте графіки зміни з часом кута повороту φ(t), кутової швидкості ω(t) і кутового прискорення β(t). Поясніть характер руху валу. 2. Визначте повне прискорення точки, що знаходиться на відстані R = 0,1 м від осі вала в момент часу t = 10 с. Кут повороту заданий у радіанах, А = 0,0314 рад/с2, B = 0,1 рад/с. β = -Acos Bt, φ(0) = 0, ω(0) = 0,1π рад/с.Задача 26580
Дано рівняння руху точки: х = 0,01t3, у = 200 - 10t. Визначити прискорення в момент часу, коли точка перетинає вісь Ох.Задача 26581
Дано рівняння руху точки: х = 8 - t2, у = t2- cos t. Визначити проекцію прискорення ау в момент часу, коли координата x = 0.Задача 26595
Матеріальна точка масою m = 0,5 кг рухається згідно векторному рівнянню r = 2 sin πti + 3 cos пtj. Визначити проекцію кількості руху точки на вісь Ох у момент часу t = 0,5 с.Задача 26596
Визначити проекцію на вісь Оу головного вектора кількості руху системи двох матеріальних точок, маси яких m1 = 4 кг, m2 = 2 кг, в момент часу, коли їх швидкості v1 = 2 м/с, v2 = 1 м/с.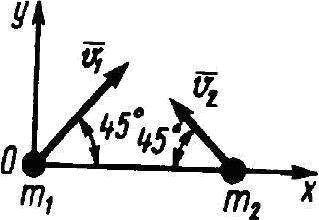
Задача 26612
Вантаж массою m = 4 кг, опускаючись вниз, призводить за допомогою нитки в обертання циліндр радіуса R = 0,4 м. Момент інерції циліндра відносно осі обертання I = 0,2 кг·м2. Визначити кінематичну енергію системи тіл в момент часу, коли швидкість вантажу v = 2 м/с.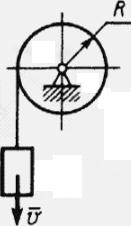
задача 13302
Кінематичні рівняння руху двох матеріальних точок мають вигляд х1 = А1+B1t+С1t2 і х2 = А2+В2t+C2t2, де (пропущено в книзі: B1 = B2), C1 = –2 м/c2, С2 = 1 м/с2. Визначте: 1) момент часу, для якого швидкості цих точок будуть рівні; 2) прискорення а1 і а2 для цього моменту.задача 13303
Радіус-вектор матеріальної точки змінюється з часом за законом r = t3i+3t2j, де i, j — орти осей х і у. Визначте для моменту часу t = 1 с: 1) модуль швидкості; 2) модуль прискорення.задача 13787
Залежність швидкості матеріальної точки від часу задана рівнянням v = 5t3 + 3t2 + 2 (м/с). Знайти прискорення в момент часу 1 с і шлях, пройдений точкою за 2 с.задача 15168
Рівняння руху матеріальної точки вздовж осі має вигляд х = А + Bt + Ct3, де А = 2 м, В = 1 м/с, С = –0,5 м/с3. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 2 с.задача 15175
Рівняння руху матеріальної точки вздовж осі має вигляд х = А – Bt + Ct3, де А = 2 м, В = 2 м/с, С = –0,5 м/с3. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 2 с.задача 15182
Рівняння руху матеріальної точки вздовж осі має вигляд х = А + Bt + Ct3, де А = 2 м, В = 2 м/с, С = –1,5 м/с3. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 2 с.задача 15192
Рівняння руху матеріальної точки вздовж осі має вигляд х = А + Bt – Ct3, де А = 2,1 м, В = 1 м/с, С = –0,8 м/с3. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 2 с.задача 15199
Рівняння руху матеріальної точки вздовж осі має вигляд х = А + Bt + Ct3, де А = 1 м, В = 2 м/с, С = 0,5 м/с3. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 2 с.задача 15206
Рівняння руху матеріальної точки вздовж осі має вигляд х = А – Bt – Ct3, де А = 2 м, В = 1 м/с, С = 0,5 м/с3. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 4 с.задача 15213
Рівняння руху матеріальної точки вздовж осі має вигляд х = А + Bt + Ct3, де А = 2 м, В = –1 м/с, С = –0,5 м/с3. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 10 с.задача 15221
Рівняння руху матеріальної точки вздовж осі має вигляд х = А + Bt + Ct2, де А = 2 м, В = 1 м/с, С = –0,5 м/с2. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 2 с.задача 15228
Рівняння руху матеріальної точки вздовж осі має вигляд х = А + Bt + Ct2, де А = –2 м, В = 1 м/с, С = 1,5 м/с2. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 20 с.задача 15233
Рівняння руху матеріальної точки вздовж осі має вигляд х = А – Bt – Ct3, де А = 2 м, В = –1 м/с, С = 0,5 м/с3. Знайти координату х, швидкість vx і прискорення ах в момент часу τ = 2 с.задача 16072
Матеріальна точка на площині здійснює рух, який задається кінематичними рівняннями: х = A·cos(ω·t); у = B·cos(ω·t + φ0), де х і у — координати точки в момент часу t, А = 4 м, В = 8 м, φ0 = π, ω = π рад/с. Визначити траєкторію точки і швидкість точки в момент часу t1 = 1 с.задача 16474
Кінематичне рівняння руху матеріальної точки вздовж прямої (вісь ОХ) задається рівнянням х = A + Bt + Сt2 + Dt3, де B = 8 м/с; С = –4 м/с2; D = 1,5 м/с3. Визначте середню швидкість і середнє прискорення матеріальної точки за проміжок часу, протягом якого точка рухається в напрямку, протилежному первісному.задача 17142
Рухи двох матеріальних точок задаються рівняннями v1(t) = B1t + C1t2, х2(t) = B2t2 + C2t3, де B1 = 8 м/с,задача 17418
Рух матеріальної точки задано рівнянням: x = A+Bt2, де А = 4 м/с, В = –0,05 м/с2. Визначити момент часу, в який швидкість точки v = 0. Знайти координату і прискорення точки в цей момент.задача 19502
Дві матеріальні точки рухаються вздовж однієї прямої з прискореннями a1 = A1+B1t, a2 = A2+B2t, де A1 = 4 м/c2, B1 = 3 м/с3, A2 = 12 м/с2, B2 = –1 м/с3. Початкові швидкості цих точок були рівні, відповідно, 8 м/с і 12,5 м/с. В який момент часу t швидкості точок будуть однакові?задача 19586
Кінематичні рівняння руху двох матеріальних точок мають вигляд: x1 = A1t + B1t2 + С1t3 і x2 = A2t + B2t2 + C2t3, де B1 = 2 м/с2, C1 = –1,5 м/с3, B2 = –1 м/с2; C2 = 0,5 м/с3. Визначте, в який момент часу прискорення цих точок однакові.задача 19741
Швидкість руху точки v = 4,9ti + 7,6j м/с. Визначте кут між вектором швидкості і віссю OX в момент часу t = 0,1 c.задача 19821
Матеріальна точка обертається навколо нерухомої осі за законом φ = A+Bt+Ct2, де A = 10 рад, B = 20 рад/с, C = –2 рад/с2 . Знайти повне прискорення точки, що знаходиться на відстані R = 0,1 м від осі обертання, для моменту часу t = 4 с.задача 19823
Матеріальна точка рухається за законом: Y(t) = At+Ct2+Bt4, де A = 6 м/с, C = 0,2 м/с2, B = –0,125 м/с4 . Знайти швидкість і прискорення точки в моменти часу t1 = 0 c і t2 = 2 с, а також середню швидкість переміщення і середнє прискорення за перші 2 с руху.задача 19824
Матеріальна точка обертається навколо нерухомої осі за законом φ = A+Ct2+Bt3, де A = 10 рад, B = 0,5 рад/с3, C = –2 рад/с2 . Знайти повне прискорення точки, що знаходиться на відстані R = 0,1 м від осі обертання, для моменту часу t = 3 с.задача 20080
Матеріальна точка здійснює коливальний рух уздовж осі ОХ за законом X = 8cos(πt+π/2), см. Знайти період коливань і прискорення точки в момент t = T/2, побудувати графік залежності x(t).задача 20190
Прискорення матеріальної точки (М.Т.) змінюється за законом: a = 1+2t м/с2. Визначити залежність x(t), якщо в початковий момент часу М.Т. перебувала в точці з координатою х0 = 5 м і мала швидкість v0 = 3 м/с.задача 20191
Прискорення матеріальної точки (М.Т.) змінюється за законом: a = 1+t2 м/с2. Визначити залежність x(t), якщо в початковий момент часу М.Т. перебувала в точці з координатою х0 = 3 м і мала швидкість v0 = 1 м/с.задача 20192
Прискорення матеріальної точки (М.Т.) змінюється за законом: a = 2+t м/с2. Визначити залежність x(t), якщо в початковий момент часу М.Т. перебувала в точці з координатою х0 = 3 м і мала швидкість v0 = 5 м/с.задача 20194
Прискорення матеріальної точки (М.Т.) змінюється за законом: a = 1+t м/с2. Визначити залежність x(t), якщо в початковий момент часу М.Т. перебувала в точці з координатою х0 = 1 м і мала швидкість v0 = 0 м/с.задача 20210
У початковий момент часу дві матеріальні точки знаходяться на деякій висоті від поверхні землі в одній точці і володіють швидкостями, відповідно рівними V01 І V02 = 45,5 М/С, спрямованими горизонтально в протилежні сторони. Через час t = 10 С після початку одночасного руху вектори швидкостей утворюють між собою кут α = 45°, а відстань між матеріальними точками стає рівною l. Визначити V01.задача 20211
У початковий момент часу дві матеріальні точки знаходяться на деякій висоті від поверхні землі в одній точці і володіють швидкостями, відповідно рівними V01 = 9,3 М/С и V02, спрямованими горизонтально в протилежні сторони. Через час t = 4 С після початку одночасного руху вектори швидкостей утворюють між собою кут α = 60°, а відстань між матеріальними точками стає рівною l. Визначити V02.задача 20212
У початковий момент часу дві матеріальні точки знаходяться на деякій висоті від поверхні землі в одній точці і володіють швидкостями, відповідно рівними V01 = 24,0 М/С и V02 = 16,0 М/С, спрямованими горизонтально в протилежні сторони. Через час t = 6 С після початку одночасного руху вектори швидкостей утворюють між собою кут α, а відстань між матеріальними точками стає рівною l. Визначити α.задача 20213
У початковий момент часу дві матеріальні точки знаходяться на деякій висоті від поверхні землі в одній точці і володіють швидкостями, відповідно рівними V01 = 42,0 М/С и V02 = 68,8 М/С, спрямованими горизонтально в протилежні сторони. Через час t після початку одночасного руху вектори швидкостей утворюють між собою кут α = 90°, а відстань між матеріальними точками стає рівною l. Визначити T.задача 20214
У початковий момент часу дві матеріальні точки знаходяться на деякій висоті від поверхні землі в одній точці і володіють швидкостями, відповідно рівними V01 = 12,0 М/С и V02 = 5,0 М/С, спрямованими горизонтально в протилежні сторони. Через час t після початку одночасного руху вектори швидкостей утворюють між собою кут α = 90°, а відстань між матеріальними точками стає рівною l. Визначити l.задача 20791
Матеріальна точка здійснює коливання за законом x(t) = Acos(ωt), де А = 4 см, ω = 2 рад/с. Визначити величину швидкості точки в той момент часу, коли її прискорення а = 2 см/с2.задача 21030
Матеріальна точка масою m = 5 кг на початку руху по горизонтальній прямій мала швидкість V0 = 3 м/с і на неї діяла сила F = 8 + 3t, яка спрямована по тій же прямій. Визначити швидкість точки в момент часу t1 = 4 с.задача 21480
Залежність координати матеріальної точки від часу виражається рівнянням: x(t) = 1,5t2–0,25t3, м. Обчисліть: 1) залежність швидкості і прискорення від часу; 2) швидкість і прискорення в момент часу t = 1 c; 3) максимальну швидкість точки; 4) переміщення через 3 с від початку руху; 5) побудуйте графіки залежностей: x = f(t), v = f(t), a = f(t); 6) назвіть характер руху тіла.задача 21672
У таблиці наведено рівняння зміни з часом кінематичних характеристик обертового маховика, закріпленого на валу двигуна. 1. Побудуйте графіки зміни з часом кута повороту φ(t), кутової швидкості ω(t) і кутового прискорення β(t). Поясніть характер руху вала. 2. Визначте повне прискорення точки, що знаходиться на відстані R = 0,1 м від осі вала в момент часу t = 10 с. Кут повороту заданий в радіанах, А = 0,0314 рад/с2, B = 0,1 рад/с. β = Ae–Bt, φ(0) = 0, ω(0) = 0.задача 21832
Рух тіла в полі Землі визначається рівняннями х(t) = 15t, y(t) = 30t–4,9t2, м. Обчисліть:1) залежність проекцій швидкості і прискорення на осі ОХ і ΟΥ від часу;
2) початкову та кінцеву швидкості руху точки;
3) запишіть рівняння траєкторії руху тіла у = f (t), побудуйте графік залежності у = f(t) для моментів часу t1 = 0 с, t2 = tподъема, t3 = tпадения і назвіть характер руху тіла;
4) максимальну висоту підйому, дальність польоту і модуль переміщення;
5) радіус кривизни у верхній точці траєкторії.
задача 21908
Матеріальна точка рухається з прискоренням, що залежать від часу a(t) = A–Bt, де А = 3 м/с2, В = 1 м/с3. Знайти залежність швидкості і координати від часу, якщо в початковий момент часу х0 = 0, v0 = 2 м/с. Знайти шлях, який пройде точка до зупинки.задача 22108
Рівняння руху матеріальної точки має вигляд x = A + Bt + Ct2 + Dt3, де A = 6 м, B = 3 м/с, C = 2 м/с2, D = 1 м/с3. В інтервалі часу t1 = 1 с до t2 = 4 с знайти: а) середню швидкість; б) середнє прискорення руху точки.задача 22882
Закон руху матеріальної точки має вигляд: r = 2ti + (2 + 3t2)j. Знайдіть проекції вектора швидкості v на осі координат та запишіть залежність вектора швидкості від часу. Обчисліть величину прискорення через 2 секунди після початку руху.задача 22933
Рух точки описується рівнянням S = 5t3–4t2+40 (у одиницях СІ). Знайдіть швидкість та прискорення точки в момент часу t1 = 2 c. Знайдіть шлях, пройдений тілом до моменту часу t2 = 3 c.задача 23066
Рівняння руху частки дано як x = sin(πt/6). Знайти моменти часу t, у які досягається максимальна швидкість частки.задача 23267
Залежність координати матеріальної точки від часу виражається рівнянням: х = 1,5t2 – 0,25t3, м. Визначити: 1) залежність швидкості та прискорення від часу; 2) швидкість та прискорення в момент часу t1 = 1 с; 3) максимальну швидкість точки; 4) переміщення через 3 с початку руху.задача 23529
Залежність координати матеріальної точки від часу виражається рівнянням: x = 3t2–0,5t3 (м). Обчисліть: 1) залежність швидкості та прискорення від часу; 2) максимальну швидкість руху точки, її переміщення через 2 с, а також швидкість та прискорення в момент часу t1 = 1 с; 3) побудуйте графіки залежності x = f(t), v = f(t) и a = f(t) для моментів часу t = 0, 1, 2, 3, 4 c.задача 23533
Матеріальна точка рухається у полі Землі згідно з рівняннями руху x(t) = 5t, y(t) = 10–4,9t2, м. Обчисліть: 1) залежність проекцій швидкості прискорення осі OX і OY від часу; 2) час руху точки; 3) запишіть рівняння траєкторії y = f(t) та визначте характер руху точки; 4) накресліть графік залежності y = f(t); 5) повне прискорення, початкову та кінцеву швидкості руху, а також модуль переміщення.задача 23535
Рух тіла у полі Землі визначається рівняннями x(t) = 10t, y(t) = 20t–4,9t2, м. Обчисліть: 1) залежність проекцій швидкості та прискорення на осі OX та OY від часу; 2) початкову та кінцеву швидкості руху; 3) рівняння траєкторії руху тіла y = f(t) та побудуйте графік залежності y = f(t) для моментів часу t1 = 0 c, t2 = tпідйому, t3 = tпадіння, Назвіть характер руху тіла. 4) максимальну висоту підйому, дальність польоту та модуль переміщення; 5) радіус кривизни у верхній точці траєкторії.задача 23586
У таблиці наведено рівняння зміни з часом кінематичних характеристик маховика, що обертається, закріпленого на валу двигуна. 1. Побудуйте графіки зміни з часом кута повороту φ(t), кутовий швидкості ω(t) та кутового прискорення β(t). Поясніть характер руху валу. 2. Визначте повне прискорення точки, що знаходиться на відстані R = 0,1 м від осі вала в момент часу t = 10 с. Кут повороту заданий у радіанах, А = 0,0314 рад/с2, B = 0,1 рад/с. β = –Asin Bt, φ(0) = 0, ω(0) = 0,1π рад/с.задача 23975
Рух тіла вздовж прямої описується рівнянням х = A+Вt+Ct2+Dt3, де A = 2 м. З моменту часу t1 = 0,7 с до t2 = 11,0 с тіло проходить шлях s. Середня швидкість та середнє прискорення на цьому інтервалі vs і as. v1 = 0,8 м/с, а1, v2 = 0,2 м/с, a2 — швидкість та прискорення у моменти часу t1 і t2. Знайти шлях s і всі швидкості та прискорення (крім заданих).задача 23988
Точка рухається прямою відповідно до рівняння x = At + Bt3, де A = 6 м/с, В = –2 м/с3. Знайти прискорення у момент, коли швидкість дорівнює нулю.задача 23989
Рух точки по кривій задано рівнянням r = iA1t3 + j(A2t2+B2t), де A1 = 1 м/с3, A2 = –1 м/с2 и B2 = 4 м/с. Знайти швидкість v у той час, коли вона паралельна осі ОХ.задача 24162
Координати x та y матеріальної точки залежать від часу за законами x = A·cos ωt, y = B·sin ωt, де A, B, ω — сталі величини. Знайдіть величину v швидкості матеріальної точки в момент ωt = π/4.задача 24511
Центрифуга, призначена для вивчення дії прискорення на організм людини, робила 12 об/хв; потім протягом 5 з число обертів центрифуги змінилося так, що на льотчика почало діяти прискорення 10g. Визначити кутове прискорення руху льотчика, якщо кабіна укріплена з відривом 7 м від осі обертання центрифуги.задача 26683
Рух матеріальної точки задано рівнянням x = At + Bt2, де A = 4 м/с, В = -0,05 м/с2. Визначити момент часу, в який швидкість v точки дорівнює нулю. Знайти координату і прискорення в цей момент.задача 40005
Кинематическое рівняння руху матеріальної точки по прямій (вісь x) має вигляд x = А+Bt+Сt2, де А = 5 м, В = 4 м/с, С = –1 м/с2. 1. Побудувати графік залежності координати x та шляхи s від часу. 2. Визначити середню швидкість <vx> за інтервал часу від t1 = 1 с до t2 = 6 с. 3. Знайти середню шляхову швидкість <v> на той же інтервал часу.задача 40797
Визначити модуль прискорення точки в момент часу 1 с, якщо рівняння руху точки x = cos πt см, y = sin πt см.Другие предметы