точка коливається період коливань визначити масу
задача 10071
На стрижні довжиною l = 30 см укріплені два однакових важка: один - в середині стрижня, другий - на одному з його кінців. Стрижень з вантажами коливається близько горизонтальної осі, що проходить чepeз вільний кінець стрижня. Визначити приведену довжину L і період Т простих гармонійних коливань даного фізичного маятника. Масою стрижня знехтувати.задача 10080
Кулька масою m = 60 г коливається з періодом T = 2 с. У початковий момент часу зміщення кульки x0 = 4,0 см і вона має енергією Е = 0,02 Дж. Записати рівняння простого гармонійного коливання кульки і закон зміни повертає сили з плином часу.задача 10567
Стрижень довжиною l = 40 см коливається біля осі, перпендикулярної стрижню і проходить чepeз його верхній кінець. Визначити період коливань такого маятника.задача 10570
Матеріальна точка масою m = 0,1 г коливається відповідно до рівняння х = Asinωt, де А = 5 см; ω = 20 с. Визначити максимальні значення повертаючої сили Fмакс і кінетичної енергії Tмакс точки.задача 10572
Диск радіусом R = 24 см коливається біля горизонтальної осі, що проходить чepeз середину одного з радіусів перпендикулярно площині диска. Визначити частоту ν коливань такого фізичного маятника.задача 11054
Математичний маятник довжиною l1 = 20 см і фізичний маятник у вигляді тонкого прямого стрижня довжиною l2 = 30 см синхронно коливаються близько однієї і тієї ж горизонтальній осі. Визначити відстань а центру мас стержня від осі коливань.задача 11334
Грузик масою m = 250 г, підвішений до пружини, коливається по вертикалі з періодом Т = 1 с. Визначити жорсткість k пружини.задача 11336
Гиря, підвішена до пружини, коливається по вертикалі з амплітудою A = 4 см. Визначити повну енергію Е коливань гирі, якщо жорсткість k пружини дорівнює 1 кН/м.задача 11339
На кінцях тонкого стрижня довжиною l = 30 см укріплені однакові важки по одному на кожному кінці. Стрижень з грузиками коливається близько горизонтальної осі, що проходить через точку, віддалену на d = 10 см від одного з кінців стрижня. Визначити приведену довжину L і період Т коливань такого фізичного маятника. Масою стрижня знехтувати.задача 11340
На стрижні довжиною l = 30 см укріплені два однакових грузика: один — в середині стрижня, інший — на одному з його кінців. Стрижень з грузиком коливається близько горизонтальної осі, що проходить через вільний кінець стрижня. Визначити приведену довжину L і період Т коливань такої системи. Масою стрижня знехтувати.задача 11342
Тонкий обруч, повішений на цвях, вбитий горизонтально в стіну, коливається в площині, паралельній стіні. Радіус R обруча дорівнює 30 см. Обчислити період Т коливань обруча.задача 11343
Однорідний диск радіусом R = 30 см коливається біля горизонтальної осі, що проходить через одну з утворюючих циліндричної поверхні диска. Який період Т його коливань?задача 11344
Диск радіусом R = 24 см коливається біля горизонтальної осі, що проходить через середину одного з радіусів перпендикулярно площині диска. Визначити приведену довжину L і період Т коливань такого маятника.задача 11345
З тонкого однорідного диска радіусом R = 20 см вирізана частина, що має вигляд кола радіусом r = 10 см, так, як це показано на малюнку. Частина диска, що залишилася, коливається відносно горизонтальної осі О, що збігається з однією з утворюючих циліндричної поверхні диска. Знайти період Т коливань такого маятника.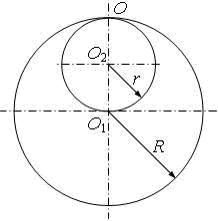
задача 11346
Математичний маятник довжиною l1 = 40 см і фізичний маятник у вигляді тонкого прямого стрижня довжиною l2 = 60 см синхронно коливаються навколо однієї і тієї ж горизонтальній вісі. Визначити відстань а центру мас стрижня від осі коливань.задача 11347
Фізичний маятник у вигляді тонкого прямого стрижня довжиною l = 120 см коливається близько горизонтальної осі, що проходить перпендикулярно стрижню через точку, віддалену на деяку відстань а від центру мас стрижня. При якому значенні а період Т коливань має найменше значення?задача 11885
Матеріальна точка бере участь у двох взаємно перпендикулярних коливаннях, що описуються в одиницях СІ рівняннями: х = 2cos (100t) і y = 3sin (50t). Визначити максимальну швидкість точки, що коливається.задача 12183
Хвилі поширюються уздовж прямої зі швидкістю 100 м/с. Яка частота коливань, якщо найменша відстань між точками, що коливаються в протилежних фазах, дорівнює 10 см?задача 12503
Координата точки масою 0,1 кг, що коливається, змінюється за законом: x = 2cos(4πt+π/4) см. Знайти швидкість точки і силу, що діє на неї через 0,5 с після початку коливань. Зобразити на малюнку залежність F(t).задача 13466
Швидкість матеріальної точки, що коливається, змінюється за законом v = vmaxcos(ωt+φ). Максимальна швидкість vmax = 10 см/с, період дорівнює 0,1 с, початкова фаза дорівнює π/2. Знайти зміщення точки в момент часу t = 0,25 с.задача 13636
Напишіть рівняння гармонійного коливання точки, якщо його амплітуда A = 15 см, максимальна швидкість коливається точки vmax = 30 см/с, початкова фаза φ = 10°.задача 13647
Повна енергія E точки, що гармонійно коливається, дорівнює 10 мкДж, a максимальна сила Fmax, діюча на точку, дорівнює -0,5 мН. Напишіть рівняння руху цієї точки, якщо період T коливань дорівнює 4 с, a початкова фаза φ = π/6.задача 13649
Визначте повну енергію матеріальної точки масою m, що коливається за законом x = А cos(ω0t + φ).задача 13650
Вантаж, підвішений до спіральної пружини, коливається по вертикалі з амплітудою А = 8 см. Визначте жорсткість k пружини, якщо відомо, що максимальна кінетична енергія Tmax вантажу становить 0,8 Дж.задача 13652
Вантаж, підвішений до спіральної пружини, коливається по вертикалі з амплітудою A = 6 см. Визначити повну енергію E коливань вантажу, якщо жорсткість k пружини становить 500 Н/м.задача 13659
Однорідний диск радіусом 20 см коливається близько горизонтальної осі, що проходить на відстані 15 см від центру диска. Визначте період коливань диска відносно цієї осі.задача 13660
Тонкий обруч радіусом R = 50 см підвішений на вбитий в стіну цвях і коливається в площині, паралельній стіні. Визначте період T коливань обруча.задача 13665
Два математичних маятника мають однакову масу, довжину, що відрізняються в n = 1,5 рази, і коливаються з однаковою кутовою амплітудою. Визначте, який маятник має більшу енергію і в скільки разів.задача 13748
На малюнку зображений графік затухаючих коливань, де S — величина, що коливається, описувана рівнянням x(t) = A0e–t/τ sin(ω1t + φ). Визначте час релаксації τ (в секундах).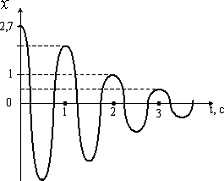
задача 14012
Рівняння коливань тіла масою 8 кг має вигляд х = 4sin(πt/4+π/3) см. Знайти повну енергію тіла, що коливається.задача 14939
Вантаж, що вільно коливається на пружині, за час 0,01 с змістився з відстані 0,5 см від положення рівноваги до найбільшої, рівної 1 см. Який період його коливань?задача 15102
Частка коливається вздовж осі х за законом х = 0,1 sin 6,28t (м). Знайдіть середнє значення модуля швидкості <v> частинки: а) за період коливання T; б) за першу 1/8 частину T; в) за другу 1/8 частину Т.задача 15422
Маса кульки дорівнює 20 г. Вона прикріплена до пружини, масою якої можна знехтувати, і коливається з періодом, рівним 0,5 с., і амплітудою, що дорівнює 6 см. Початкова фаза дорівнює π/6. Знайти швидкість і прискорення в момент часу, рівний Т/2, коефіцієнт k у виразі для повертаючої сили і написати рівняння коливань.задача 15477
Амплітуда гармонійного коливання A = 5 см, період T = 4 с. Знайти максимальну швидкість vmax точки, що коливається, і її максимальне прискорення amах.задача 15489
Амплітуда гармонічних коливань матеріальної точки А = 2 см, повна енергія коливань W = 0,3 мкДж. При якому зміщенні х від положення рівноваги на коливається точку діє сила F = 22,5 мкн?задача 15614
Ліфт, в якому коливається математичний маятник, опускається з прискоренням а = 3 м/с2. Визначити період коливань Т маятника. Його довжина дорівнює 1 м.задача 15898
Визначити максимальні значення швидкості і прискорення тіла, що коливається, якщо рівняння коливань тіла має вигляд, м: x = 0,04sin(πt/2+π/4).задача 15900
До пружини підвішений вантаж масою m = 0,02 кг. Знаючи, що максимальна кінетична енергія гармонічних коливань вантажу Wк max = 1 Дж, знайти, при якому зміщенні від положення рівноваги на коливний вантаж діє сила F = 10 Н. Амплітуда коливань A = 0,05 м.задача 15926
Товстостінне кільце з радіусами R1 = 10 см і R2 = 20 см коливається близько горизонтальній осі, віддаленій від центру кільця на відстані d = R1. Визначити період коливань такого маятника.задача 15929
Куля радіуса 40 см коливається біля осі, що проходить горизонтально через кулю на відстані 30 см від центру кулі. Знайти період коливань цього маятника.задача 16044
Пружинний маятник масою m = 100 г, що коливається з амплітудою A = 1 см, має максимальну потенційну енергію 5 Дж. Знайти період коливань маятника.задача 16046
Вантаж масою 100 г коливається на пружині жорсткістю k = 10 Н/м з амплітудою 5 см. Знайти максимальну швидкість вантажу.задача 16104
Математичний маятник коливається відповідно до рівняння х = 0,8sin(2πt + π). Маса вантажу m = 120 г.Найдите
1. Амплітуду коливань.
2. Циклічну частоту коливань.
3. Період коливань.
4. Частоту коливань.
5. Фазу коливань.
6. Початкову фазу коливань.
7. Довжину нитки.
8. Рівняння залежності швидкості від часу.
9. Рівняння залежності прискорення від часу.
10. Максимальну швидкість тіла.
11. Максимальну кінетичну енергію тіла.
12. Максимальну потенційну енергію тіла.
13. Максимальну висоту підйому тіла від положення рівноваги (для варіантів з математичним маятником).
14. Повну енергію тіла.
15. Момент часу, в який зсув точки, що коливається, дорівнює половині амплітуди.
Постройте графіки
• х(t)
• υ(t)
• a(t)
задача 16450
Через диск радіусом R і масою M проходить вісь перпендикулярно площині диска на відстані r від його центру. З яким періодом повинен коливатися диск щодо заданої осі?задача 16631
Матеріальна точка масою m = 0,1 кг коливається так, що проекція ах прискорення залежить від часу відповідно до рівняння ах = 10sin(2πt/10), м/с2. Знайдіть величину проекції сили на вісь ОХ, що діє на матеріальну точку в момент часу t = 5/6 с.задача 17201
Система з трьох вантажів, з'єднаних стрижнями довжиною l = 30 см (рис.), коливається відносно горизонтальної осі, що проходить через точку О перпендикулярно площині креслення. Знайти період Т коливань системи. Масами стрижнів знехтувати, вантажі розглядати як матеріальні точки.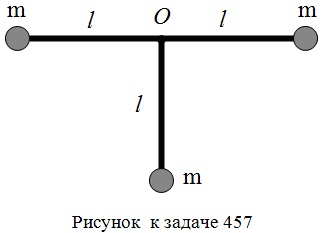
задача 17997
Маятник (у вигляді букви Т) виготовлений з двох однорідних стрижнів довжиною l і масою m. Він коливається навколо горизонтальної осі, що проходить через середину одного зі стрижнів (точка О). Визначити момент сили тяжіння відносно точки О і кутове прискорення маятника в момент часу, коли він відхилений з положення рівноваги на 30°. Вважати, що маятник обертається без тертя.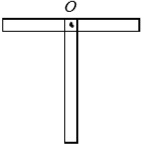
задача 18131
Матеріальна точка масою 0,1 г коливається відповідно до рівняння х = A sin ωt, де А = 10 см, ω = 25 рад/с. Визначити максимальні значення повертаючої сили і кінетичної енергії точки.задача 18135
Амплітуда гармонічних коливань матеріальної точки 3 см, повна енергія коливань 5·10–7 Дж. Знайти зміщення коливної точки, при якому на неї діє сила 2,5·10–5 Н.задача 18217
Уздовж осі X поширюється плоска хвиля з довжиною хвилі λ. Яка найменша відстань Δx між точками середовища, які коливаються в протифазі?задача 19724
В отворі укладаються три зони Френеля. Вкажіть неправильне твердження.1) Вторинні джерела в точках В і С коливаються в протифазі.
2) Коливання, що приходять в точку Р екрану від точок В і С зрушені по фазі на Δφ = π.
3) У точці Р спостерігається максимум освітленості.
4) Коливання від точок В і С приходять в точку Р екрану, маючи різницю ходу Δ = λ/2.
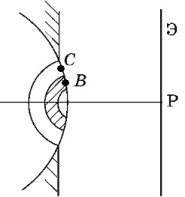
задача 19855
Маятник (у вигляді букви Т) виготовлений з двох однорідних стрижнів довжиною l і масою m. Він коливається навколо горизонтальної осі, що проходить на відстані l/4 від кінця одного зі стрижнів (точка О). Визначити момент сили тяжіння відносно точки О і кутове прискорення маятника в момент часу, коли він відхилений з положення рівноваги на 90°. Вважати, що маятник обертається без тертя.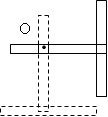
задача 19856
Маятник (у вигляді букви Т) виготовлений з двох однорідних стрижнів довжиною l і масою m. Він коливається навколо горизонтальної осі, що проходить через кінець одного зі стрижнів (точка О). Визначити момент сили тяжіння відносно точки О і кутове прискорення маятника в момент часу, коли він відхилений з положення рівноваги на 90°. Вважати, що маятник обертається без тертя.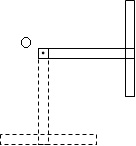
задача 20108
Написати рівняння гармонійного коливання, якщо амплітуда його 10 см, максимальна швидкість 50 см / c, початкова фаза 15 °. Визначити період коливання і зсув точки, що коливається, чepeз 0,2 с від початку коливання.задача 20117
Хвиля поширюється по прямій зі швидкістю 20 м/с. Дві точки, що знаходяться на цій прямій на відстані 12 і 15 м від джерела коливань, коливаються за законом синуса з амплітудами, рівними 0,1 м, і з різницею фаз 135 °. Знайти довжину хвилі, написати її рівняння і знайти зміщення вказаних точок у момент часу t = 1,2 с.задача 20810
Матеріальна точка масою m = 10 г виконує гармонічні коливання за законом косинуса з періодом Т = 2 с і початковою фазою, що дорівнює нулю. Повна енергія коливається точки W = 0,1 МДж. Записати рівняння даних коливань. Визначити найбільше значення сили Fmax, діючої на точку.задача 21032
На малюнку показано напрямок швидкості двох точок струни, що коливається. В якому напрямку поширюється хвиля?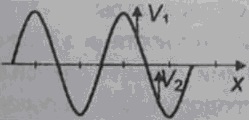
задача 21271
Математичний маятник довжиною 40 см і фізичний маятник у вигляді тонкого прямого стрижня довжиною 30 см, коливаються синхронно. Визначити відстань від центру мас стержня від точки підвісу.задача 21342
Швидкість матеріальної точки, що коливається, змінюється за законом v = vmaxcos(ωt). Максимальна швидкість vmax = 5 см/с, період дорівнює 0,1 с. Знайти прискорення точки в момент часу t = 0,25 с.задача 21344
Вантаж масою 360 г коливається в маслі на пружині з жорсткістю k = 0,568 Н / см. Сила опору пропорційна та обернена за знаком до швидкості вантажу. Вважаючи, що коефіцієнт пропорційності r = 1,44 Н·с/м, скласти на основі 2-го закону Ньютона диференціальне рівняння коливань вантажу, записати його рішення в загальному вигляді і з числовими коефіцієнтами. Знайти циклічну частоту і період згасаючих коливань.задача 21354
Кулька масою 100 г коливається з періодом 12 с. У початковий момент часу зміщення кульки x0 = 40 см і він має енергію Е = 200 Дж. Записати рівняння простого гармонійного коливання кульки і закон зміни повертаючої сили з плином часу.задача 22424
Два когерентних джерела звуку коливаються в однаковій фазі. У точці, віддаленій від першого джерела на 1 м, а від другого на 1,5 м, звук не чути. Визначити частоту коливань джерел. Швидкість звуку дорівнює 330 м/с.задача 23286
Айсберг у вигляді прямої призми коливається вздовж вертикальної осі. Визначити період Т малих коливань айсберга, якщо висота надводної частини перебуває у стані рівноваги h = 100 м.задача 23608
Математичний маятник масою m і довжиною L коливається згідно із законом X = X0 sin(ωt + φ). Знайти натяг нитки та її кінетичну енергію в момент часу t.задача 23696
Рівняння загасаючих коливань дано у вигляді х = 5е–0,25t sin (π/2) м. Знайти швидкість точки, що коливається в моменти часу: 0, Т, 2Т.задача 24097
Матеріальна точка масою 10 г коливається згідно із законом x = 0,2sin(πt), м. Визначити величину повертаючої сили в момент часу t = 0,1 с та повну енергію точки.задача 24102
Суцільний мідний диск масою 1 кг і товщиною 1 см коливається біля горизонтальної осі, що проходить через середину одного з радіусів перпендикулярно площині диска. Визначити період такого фізичного маятника.задача 24253
Після першого коливання енергія системи, що коливається, зменшилася на соту частину від початкової. Визначте коефіцієнт загасання, якщо період коливань дорівнює 0,1 с.задача 24747
На малюнку зображено графік загасаючих коливань, де S - величина, що коливається, описується рівнянням х(t) = A0e–t/Tsin(ω1t+φ). Визначити коефіцієнт згасання (в с–1).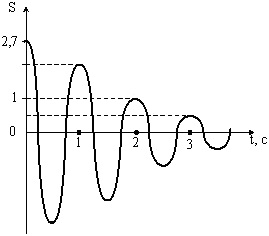
задача 25086
Залежність координати тіла, що коливається, від часу представлена графіком на малюнку. Напишіть у СІ рівняння гармонійних коливань у вигляді x = Asin(ωt + φ). Побудуйте графіки, що відображають залежність проекції швидкості vx та проекції прискорення ax від часу.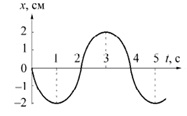
задача 26139
Плоска хвиля поширюється вздовж осі х зі швидкістю u = 10 м/с. Амплітуда коливань частинок середовища дорівнює А = 3 см. Дві точки, що знаходяться від джерела коливань на відстані х1 = 6 м і х2 = 8 м, коливаються з різницею фаз Δφ = π/3. Визначити довжину хвилі λ і зсув ξ даних точок в момент часу t = 2 с.задача 26146
Плоска хвиля поширюється вздовж осі х зі швидкістю u = 5 м/с. Амплітуда коливань частинок середовища дорівнює А = 4 см. Дві точки, що знаходяться від джерела коливань на відстані х1 = 7 м і х2 = 10 м, коливаються з різницею фаз Δφ = π/65. Визначити довжину хвилі λ і зсув ξ даних точок в момент часу t = 4 с.задача 26196
Плоска хвиля поширюється вздовж осі x зі швидкістю u = 5 м/c. Амплітуда коливань частинок середовища дорівнює A = 4 см. Дві точки, що знаходяться від джерела коливань на відстані x1 = 7 м і x2 = 10 м, коливаються з різницею фаз Δφ = 6π/5. Визначити довжину хвилі λ і зсув ξ даних точок в момент часу t = 4 с.задача 26416
Кінець гілки камертона коливається з частотою 500 Гц і амплітудою 0,2 мм. Визначити: а) середню швидкість при русі від крайнього положення до положення рівноваги; б) середню швидкість при проходженні 0,1 мм, починаючи від крайнього положення; в) середню швидкість при проходженні 0,1 мм, починаючи від положення рівноваги; г) максимальну швидкість.задача 26456
Спіральна пружина під дією підвішеного до неї вантажу розтягнулася на 6,5 см. Якщо вантаж відтягнути вниз, а потім відпустити, то він почне коливатися уздовж вертикальної лінії. Визначити період коливань вантажу.задача 26493
Однорідний стрижень довжини l коливається відносно горизонтальної осі, перпендикулярної стрижню і яка знаходиться на відстані x від його центру мас. Покажіть, що період коливань буде мінімальним, якщо x = l/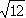 .
.
задача 26696
Суцільний однорідний диск радіусом R = 0,1 M коливається близько осі, перпендикулярної до площини диска і проходить через край диска. Якої довжини має бути математичний маятник, що має той же період коливань, що і диск?задача 40035
Матеріальна точка масою m = 5 г здійснює гармонійні коливання з частотою ν = 0,5 Гц. Амплітуда коливань А = 3 см. Визначити: 1) швидкість v точки в момент часу, коли зсув x = 1,5 см; 2) максимальну силу Fmах, діючу на точку; 3) повну енергію E точки, що коливається.задача 40143
Грузик масою 250 г, підвішений до легкої пружини, коливається по вертикалі з частотою 1 Гц. Визначити період коливань важка і жорсткість пружини.задача 40636
Матеріальна точка масою m = 10 г здійснює гармонійні коливання з частотою v = 0,2 Гц. Амплітуда коливань дорівнює 5 см. Визначити: 1) максимальну силу, що діє на точку, 2) повну енергію точки, що коливається.задача 40637
Запишіть рівняння гармонійного коливання матеріальної точки, якщо його амплітуда А = 10 см, максимальна швидкість точки, що коливається, vmax = 20 см/с, початкова фаза 15°.задача 40643
Матеріальна точка коливається по гармонійному закону, при цьому максимальне відхилення її від положення рівноваги дорівнює 3 см, а повна енергія коливань 2,25·10–4 Дж. При якому зміщенні від положення рівноваги на точку, що коливається, діє сила, рівна 1,27·10–4 Н?задача 40731
Матеріальна точка, маса якої m = 4 г, коливається з амплітудою X0 = 4 см і частотою ν = 0,5 Гц. Яка швидкість точки в положенні, де зсув Х = 2 см?задача 40767
Рух тіла масою 2 кг описується законом х = 0,8 sin(πt+0,5π). Визначити енергію тіла, що коливається і максимальну силу, що діє на нього.задача 40814
Чому дорівнює максимальне значення швидкості точки, що коливається за законом x=0,01cos(10t+π)?Другие предметы