знайти результуючу амплітуду коливань однаковий фаза два
задача 10078
Складаються два коливання однакового напрямку і однакового періоду: х1 = А1sinω1t і x2 = A2sinω2(t+τ), де А1 = A2 = 3 см, ω1 = ω2 = π c–1, τ = 0,5 c. Визначити амплітуду А і початкову фазу φ0 результуючого коливання. Написати його рівняння. Побудувати векторну діаграму для моменту часу t = 0.задача 10575
Складаються два коливання однакового напрямку і однакового періоду: х1 = А1sin ω1t і х2 = А2sin ω2(t+τ), де A1 = 1 см; ω1 = ω2 = π c–1; τ = 0,5 c. Визначити амплітуду A і початкову фазу φ0 результуючого коливання. Написати його рівняння.задача 11314
Визначити амплітуду А і початкову фазу φ результуючого коливання, що виникає при складанні двох коливань однакових напрямків і періодів: x1 = A1sinωt і x2 = A2sinω(t+τ), де A1 = A2 = 1 см; ω = π с–1; τ = 0,5 с. Знайти рівняння результуючого коливання.задача 11315
Точка бере участь у двох однаково спрямованих коливаннях: x1 = A1sinωt і x2 = A2cosωt, де А1 = 1 см; A2 = 2 см; ω = 1 с–1. Визначити амплітуду А результуючого коливання, його частоту ν і початкову фазу φ. Знайти рівняння цього руху.задача 12187
Точка бере участь у двох однаково спрямованих коливаннях х1 = А 1·sin ωt і x2 = A2·sin ωt, де А1 = 1 см, A2 = 2 см, ω = 1 рад/с. Визначити амплітуду результуючого коливання. Записати рівняння коливань.задача 12468
Скласти два коливання: x1 = 5 cos14t і x2 = 4cos12t. Знайти період биття і період результуючого коливання.задача 12876
Грузик, підвішений на легкій пружині, здійснює Гармонійні коливання у вертикальній площині з амплітудою 5 см. У певний момент точка підвісу сама починає коливатися у вертикальній площині з амплітудою 5 см і тим же періодом. Знайти різницю фаз коливань, якщо амплітуда результуючого коливання дорівнює 10 см.задача 12983
Електростатичне поле створено в вакуумі позитивними точковими зарядами 2q і 3q. Знайдіть, як і у скільки разів зміниться напруженість результуючого поля в точці А, що лежить посередині між зарядами, якщо заряд 2q замінити зарядом –2q.задача 12991
У вершинах прямокутника зі сторонами а = 6 см і b = 8 см розташовані два позитивних і два негативних точкових заряди, причому q1 = q2 = 2 нКл, q3 = q4 = –2 нКл. Знайти напруженість результуючого поля в точці перетину діагоналей прямокутника.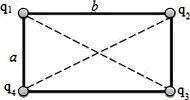
задача 13035
В результаті складання двох однаково спрямованих гармонічних коливань з однаковими амплітудами і однаковими періодами виходить результуюче коливання з тим же періодом і тієї ж амплітудою. Знайти різницю фаз коливань (в градусах).задача 13681
Складаються два гармонійних коливання одного напрямку, описуваних рівняннями х1 = 3соs2πt, см х2 = 3 cos(2πt + π/4), см. Визначте для результуючого коливання: 1) амплітуду; 2) початкову фазу. Запишіть рівняння результуючого коливання і уявіть векторну діаграму складання амплітуд.задача 13685
Складаються два гармонійних коливання одного напрямку, що мають однакові амплітуди і однакові початкові фази, з періодами T1 = 2 с і Т2 = 2,05 c. Визначте: 1) період результуючого коливання; 2) період биття.задача 14264
Запишіть умову максимального посилення при накладенні двох когерентних світлових хвиль 1 і 2 через їх різницю фаз Δφ. Яке співвідношення між інтенсивністюзадача 14623
Два точкових електричних заряди q1 = +5q и q2 = –2q знаходяться на відстані r = 10 см один від одного. Знайдіть, на якій відстані x від заряду q1 напруженість Ex результуючого електростатичного поля дорівнює нулю.задача 14633
У вакуумі на відстані r = 10 см один від одного розташовані два точкових заряди q1 = –10 нКл і q2 = 6 нКл. Відстань АВ = 5 см, ε = 1. Чому дорівнює потенціал результуючого поля в точці В?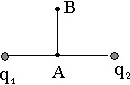
задача 15045
Амплітуда результуючого коливання, що виходить при додаванні двох однаково спрямованих гармонічних коливань однакової частоти, що мають різницю фаз 60°, дорівнює 6 см. Визначити амплітуду другого коливання, якщо А1 = 5 см.задача 15177
В центр квадрата, в вершинах якого знаходиться по заряду q = 1,2·10–9 Кл, поміщений негативний заряд. Знайти величину цього заряду Q, якщо результуюча сила F, що діє на кожен заряд q, дорівнює нулю.задача 15184
В центр квадрата, в вершинах якого знаходиться по заряду q = –2·10–9 Кл, поміщений негативний заряд. Знайти величину цього заряду Q, якщо результуюча сила F, що діє на кожен заряд q, дорівнює нулю.задача 15208
В центр шестикутника, в вершинах якого знаходиться по заряду q = 2·10–9 Кл, поміщений негативний заряд. Знайти величину цього заряду Q, якщо результуюча сила F, що діє на кожен заряд q, дорівнює нулю.задача 15501
Знайти амплітуду А і початкову фазу φ гармонійного коливання, отриманого від складання однаково спрямованих коливань, даних рівняннями x1 = 4sin πt см і х2 = 3sin(πt+π/2) см. Написати рівняння результуючого коливання. Дати векторну діаграму додавання амплітуд.задача 15506
Точка бере участь у двох коливаннях однакового періоду з однаковими початковими фазами. Амплітуди коливань рівні A1 = 3 см і A2 = 4 см. Знайти амплітуду А результуючого коливання, якщо коливання відбуваються; а) в одному напрямку; б) у двох взаємно перпендикулярних напрямках.задача 16076
Два заряди q і 2q закріплені на відстані 1 см один від одного. Визначити, в якій точці на прямій, що проходить через заряди, слід помістити третій заряд, щоб результуюча сила, що діє на кожен заряд, дорівнювала нулю. Знайти знак і величину цього заряду.задача 16130
Точка бере участь в трьох коливаннях, що відбуваються по одній прямій і виражених рівняннями x1 = 3cost, x2 = 3cos(t+π/3), x3 = 3sin(t+7π/6) (зміщення надані в см). Визначити амплітуду і початкову фазу результуючого коливання. Написати його рівняння руху.задача 16479
Три однакові заряди величиною q = 10 нКл розташовані в вершинах правильного трикутника зі стороною 1 см. Який негативний заряд потрібно помістити в центр трикутника, щоб результуюча сила, що діє на кожен заряд, дорівнювала нулю.задача 16489
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються вздовж одного напрямку. Частота 4 Гц однакова для обох коливань, початкові фази мають значення π/12 рад і 7π/12 рад, а амплітуди відповідно рівні 5 см і 5 см. Запишіть рівняння вихідних коливань. Знайдіть амплітуду і початкову фазу результуючого коливання. Запишіть рівняння для швидкості результуючого коливання, якщо маса частинки 25 г.задача 16563
Скласти два коливання х1 = 2 cos 28t і х2 = 4 cos 26t. Знайти період биття і період результуючого коливання.задача 16583
Використовуючи векторну діаграму, скласти 5 співнапрямлених коливань:x1 = 2·cos(ω·t), мм;
х2 = 2·sin(ω·t), мм;
x3 = 2·cos(ω·t + π/4), мм;
x4 = 2·cos(ω·t + 3π/4), мм;
x5 = 2·cos(ω·t + 5π/4), мм.
Записати рівняння результуючого коливання.
задача 17163
Точка бере участь в двох взаємно перпендикулярних коливаннях х = 2sin(ωt) м і y = cos(ωt) м. Знайдіть траєкторію результуючого руху точки.задача 17636
Написати рівняння результуючого коливання, отриманого в результаті складання двох взаємно перпендикулярних коливань з однаковими частотами ν = 5 Гц і з однаковою початковою фазою ψ1 = ψ2 = π/3. Амплітуди коливань рівні А1 = 0,01 м і А2 = 0,05 м.задача 17919
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються вздовж одного напрямку. Частота 8 Гц однакова для обох коливань, початкові фази мають значення π/2 рад і π рад, а амплітуди відповідно рівні 11 см і 11 см. Запишіть рівняння вихідних коливань. Знайдіть амплітуду і початкову фазу результуючого коливання. Запишіть його рівняння.задача 17956
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються вздовж одного напрямку. Частота 5 Гц однакова для обох коливань, початкові фази мають значення π/6 рад і –π/6 рад, а амплітуди відповідно рівні 8 см і 10 см. Запишіть рівняння вихідних коливань. Знайдіть амплітуду і початкову фазу результуючого коливання, запишіть його рівняння і побудуйте графік від часу.задача 17962
Використовуючи векторну діаграму, скласти 6 співнапрямлених коливань:задача 17964
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються вздовж одного напрямку. Частота 6 Гц однакова для обох коливань, початкові фази мають значення 3π/4 ραд і 5π/4 рад, а амплітуди відповідно рівні 6 см і 6 см. Запишіть рівняння вихідних коливань. Знайдіть амплітуду і початкову фазу результуючого коливання, запишіть його рівняння.задача 17967
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються по взаємно перпендикулярним напрямам. Задані частоти коливань ν1 = 3 Гц, ν2 = 3 Гц, їх амплітуди А1 = 4 А2 = 6 см і початкові фази π/4 рад і 7π/12 рад. Напишіть рівняння вихідних коливань. Знайдіть рівняння траєкторії результуючого руху в координатах XOY і побудуйте її графік. Вкажіть на графіку положення частинки в початковий момент часу і напрямок руху по траєкторії.задача 17969
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються по взаємно перпендикулярним напрямам. Задані частоти коливань ν1 = 4 Гц і ν2 = 4 Гц. Їх амплітуда А1 = 5 см, А2 = 8 см і початкові фази π/2 рад і π/2 рад. Напишіть рівняння вихідних коливань. Знайдіть рівняння траєкторії результуючого руху в координатахзадача 17975
За допомогою векторної діаграми скласти 3 співнапрямлені коливання: х1 = 3·cos(ω·t), см; x2 = 3·sin(ω·t), см; х3 = 6·sin(ω·t + π), см. Записати рівняння результуючого коливання, якщо ω = π/2 рад/с. Побудувати графік залежності хрез від часу.задача 17979
При додаванні гармонічних коливань з близькими частотами рівняння результуючих коливань (биття) має вигляд: х = 10·cos(4t)·cos(104t) мм. Визначити частоти коливань, і записати рівняння цих коливань.задача 17980
При додаванні гармонічних коливань з близькими частотами рівняння результуючих коливань має вигляд: х = 10·cos(4t)·cos(104t) мм. Визначити частоти коливань, і записати рівняння цих коливань. Скільки коливань здійснює коливання точка за час, що дорівнює періоду биття?задача 18216
Дві плоскі синусоїдальні хвилі, амплітуди яких однакові, а частоти відповідно ν і ν+Δν (Δν << ν), накладаються одна на одну. Яка максимальна амплітуда результуючої хвилі? Який розподіл середньої щільності енергії вздовж напрямку поширення хвилі?задача 19164
Знайти амплітуду і початкову фазу α коливань, які утворюються в результаті додавання наступних коливань одного напрямку: x1 = 20 cos ωt (мм), x2 = 20 cos(ωt + π/3) (мм), де ω = π с–1. Написати рівняння результуючих коливань x(t).задача 19168
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються вздовж одного напрямку. Частота 3 Гц однакова для обох коливань, початкові фази мають значення 3π/4 рад і π рад, а амплітуди відповідно рівні 7 см і 4 см. Запишіть рівняння вихідних коливань. Знайдіть амплітуду і початкову фазу результуючого коливання. Запишіть його рівняння. Знайдіть енергію частинки, якщо її маса 15 г.задача 19180
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються вздовж одного напрямку. Частота 5 Гц однакова для обох коливань, початкові фази мають значення π/6 рад і –π/6 рад, а амплітуди відповідно рівні 8 см і 10 см. Запишіть рівняння вихідних коливань. Знайдіть амплітуду і початкову фазу результуючого коливання. Запишіть його рівняння. Знайдіть рівняння швидкості результуючого руху.задача 19190
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються по взаємно перпендикулярним напрямам. Задані частоти коливань ν1 = 14 Гц, ν2 = 14 Гц, їх амплітуди А1 = 15 см, А2 = 20 см і початкові фази π/2 рад і π/4 рад. Напишіть рівняння вихідних коливань. Знайдіть рівняння траєкторії результуючого руху в координатах ХОУ і побудуйте її графік. Вкажіть на графіку положення частинки в початковий момент часу і напрямок руху по траєкторії.задача 19254
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються вздовж одного напрямку. Частота 2 Гц однакова для обох коливань, початкові фази мають значення 4π/3 рад і 2π/3 рад, а амплітуди відповідно рівні 7 см і 4 см. Запишіть рівняння вихідних коливань. Знайдіть амплітуду і початкову фазу результуючого коливання. Запишіть його рівняння. Знайдіть період результуючих коливань.задача 19620
Використовуючи векторну діаграму, скласти 6 співнапрямлених коливань:x1 = 3·cos(ω·t);
x2 = 3·cos(ω·t + π/2);
x3 = 4·cos(ω·t – π/2);
x4 = 4·cos(ω·t + π);
x5 = sin(ω·t);
x6 = sin(ω·t + π/2).
Записати рівняння результуючого коливання (x1, x2 ..., x6 вимірюються в см).
задача 19960
Написати рівняння руху, що виходить в результаті складання двох однаково спрямованих гармонічних коливань, заданих рівняннями х1 = 4sinπt см і х2 = 3sin(πt+π/3) см. Написати рівняння результуючого коливання. Побудувати векторну діаграму додавання амплітуд.задача 20381
Матеріальна точка бере участь одночасно в двох коливаннях одного напрямку x1 = 5 sin (2t + π/4), см и х2 = 15 sin 2t, см. Записати рівняння результуючого коливання. Визначити швидкість точки через 0,2 с.задача 20382
Складаються два коливання одного напрямку, що відбуваються за законом косинуса, з однаковими амплітудами 0,1 м і однаковими початковими фазами, частоти яких становлять відповідно 50 і 50,6 Гц. Записати рівняння результуючого коливання.задача 20563
Складаються два коливання однакового напрямку і однакової частоти. Закони коливань мають вигляд: x1(t) = 3cos(5πt + π/6), x2(t) = 2sin(5πt – 2π/3). Визначити амплітуду, період і початкову фазу результуючого коливання. Записати закон результуючого коливання, зобразити коливання у вигляді векторів на координатній площині.задача 20696
Складаються два коливання однакового напрямку і однакової частоти. Закони коливань мають вигляд: x1(t) = sin(πt + π/4), x2(t) = 3sin(πt + π/6). Визначити амплітуду, період і початкову фазу результуючого коливання. Записати закон результуючого коливання, зобразити коливання у вигляді векторів на координатній площині.задача 20812
Складаються два гармонійних коливання, що відбуваються в одному напрямку: x1 = 2cos2πt см і x2 = 2cos(2πt+π/3) см. Напишіть рівняння результуючого коливання і побудуйте векторну діаграму додавання амплітуд.задача 20824
Складаються три гармонійних коливання одного напрямку з однаковими періодами. Амплітуди і початкові фази коливань рівні: А1 = 3 см, φ1 = 0; А2 = 1 см, φ2 = π/2 ; А3 = 2 см, φ3 = π. Побудувати векторну діаграму додавання амплітуд, визначити амплітуду і фазу результуючого коливання і записати його рівняння.задача 21126
Складаються два коливання одного напрямку і періоду. Амплітуди коливань, що додаються, дорівнюють: A1 = 2 см, А2 = 4 см. Початкові фази коливань φ1 = 30°, φ2 = 60°. Визначити амплітуду і початкову фазу результуючого коливання. Побудувати векторну діаграму.задача 21159
Амплітуди і періоди двох однаково спрямованих гармонічних коливань рівні, а фази розрізняються на 2π/3. Рівняння результуючого коливання в одиницях СІ має вигляд x = 0,2cos(πt+π). Визначити рівняння складових коливань.задача 21426
Матеріальна точка бере участь у двох коливаннях, що відбуваються по одній прямій і виражаються рівняннями x1 = cos t см и х2 = 2 sin t см. Знайти амплітуду A результуючого коливання, його частоту ν і початкову фазу φ. Написати рівняння руху.задача 21745
Два когерентних джерела звукових хвиль знаходяться на відстанях 3,5 м і 2,3 м від мікрофона. Обчисліть відношення амплітуди результуючого і вихідного коливань. Довжина хвилі дорівнює 0,30 м. Як зміниться амплітуда результуючого коливання, якщо відстань до першого джерела зменшити до 3,05 м?задача 21755
Частка одночасно бере участь у двох коливаннях одного напрямку: x1 = 4cos4πt (см) і x2 = 3cоs(4πt + π/2) (см). Знайти циклічну частоту ω, амплітуду А і початкову фазу α результуючого коливання частки. Побудувати векторну діаграму.задача 22224
Мембрана мікрофона бере участь в двох коливаннях: x1 = 3cos(400t), мм; x2 = 3cos(405t), мм. Записати рівняння результуючого коливання, визначити амплітуду, частоту і період биття.задача 22227
Скласти 18 співнапрямлених коливань, фаза кожного наступного коливання зрушена щодо фази попереднього коливання на π/3. Написати рівняння результуючого коливання, якщо амплітуди всіх коливань А1 = 2 см, а період коливань дорівнює 0,2 с.задача 22228
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються по взаємно перпендикулярним напрямам. Задані частоти коливань ν1 = 13 Гц, ν2 = 13 Гц, їх амплітуди А1 = 14 см, А2 = 18 см і початкові фази π/3 рад і π/6 рад. Напишіть рівняння вихідних коливань. Знайдіть рівняння траєкторії результуючого руху в координатах XOY і побудуйте її графік. Вкажіть на графіку положення частинки в початковий момент часу і напрямок руху по траєкторії.задача 22446
Використовуючи векторну діаграму скласти 3 співнапрямлених коливань: х1 = 3sin(ωt), см; х2 = 4cos(ωt), см; х3 = 5cos(ωt + 3π/4), см. Записати рівняння результуючого коливання, якщо ω = 2 paд/c.задача 22447
Використовуючи векторну діаграму скласти 3 співнапрямлених коливань: х1 = 3sin(ωt), см; х2 = 4cos(ωt), см; х3 = 5cos(ωt + 3π/4), см. Записати рівняння результуючого коливання, якщо ω = 2 paд/c.задача 22500
В точку спостереження приходять коливання від двох джерел: y1 = 2,3cos(2,4t–5,8) и y2 = 6,8cos(2,4t+1,9). Яка буде амплітуда результуючого коливання?задача 22569
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються по взаємно перпендикулярним напрямам. Задані частоти коливань ν1 = 2 Гц, ν2 = 2 Гц, їх амплітуди А1 = 3 см, А2 = 7 см і початкові фази π/2 рад и 4π/3 рад. Напишіть рівняння початкових коливань. Знайдіть рівняння траєкторії результуючого руху в координатах ХOΥ і побудуйте її графік. Вкажіть на графіку положення частинки в початковий момент часу і напрямок руху по траєкторії.задача 22570
Точка бере участь в двох гармонійних коливаннях одного напрямку: x1 = 3·cos(10πt + π/2), см; х2 = 4·cos(10πt+π/3), см. Записати рівняння результуючого коливання.задача 22571
Тіло масою 120 г бере участь одночасно в двох гармонійних коливаннях, що відбуваються вздовж одного напрямку. Частота 7 Гц однакова для обох коливань, початкові фази мають значення 2π/3 рад і -π/3 рад, а амплітуди відповідно рівні 10 см і 5 см. Запишіть рівняння початкових коливань. Знайдіть амплітуду і початкову фазу результуючого коливання, запишіть його рівняння. Знайдіть коливальну енергію тіла.задача 22572
Частка бере участь одночасно в двох гармонійних коливаннях, що відбуваються по взаємно перпендикулярним напрямам. Задані частоти коливань ν1 = 20 Гц, ν2 = 20 Гц, їх амплітуди А1 = 10 см, А2 = 20 см і початкові фази π/2 рад і π/4 рад. Напишіть рівняння початкових коливань. Знайдіть рівняння траєкторії результуючого руху в координатах ХОУ і побудуйте її графік. Вкажіть на графіку положення частинки в початковий момент часу і напрямок руху по траєкторії.задача 22574
За допомогою векторної діаграми скласти три співнапрямлені коливання з рівними частотами, співвідношення між амплітудами яких має вигляд: А1 : А2 : А3 = 3 : 2 : 1. Визначити амплітуду результуючого коливань, якщо початкові фази вихідних коливань дорівнюють нулю, а амплітуда першого коливань А1 = 1 см. Записати рівняння результуючого коливання і побудувати графік залежності від часу, якщо період коливань дорівнює 2 с.задача 22576
Складаються два співнапрямлені коливання з амплітудами А1 = А2 = 1 см. Амплітуда результуючого коливання дорівнює 1 см. Записати рівняння вихідних коливань, якщо початкова фаза першого коливання α1 = 0, а періоди обох коливань однакові і рівні 0,1 с.задача 22577
Складаються три гармонічних коливання одного напрямку з однаковими періодами по 2 с кожний і однаковими амплітудами кожна по 3 см. Початкові фази коливань дорівнюють відповідно нулю, π/3 рад и 2π/3 рад. Запишіть рівняння результуючого коливання.задача 22578
Складаються чотири співнапрямлені коливання: x1 = 2cos(πt), мм, x2 = 2cos(πt + π/6), мм, x3 = 2sin(πt), мм, x4 = 2sin(πt – π/3), мм. Для складання застосувати метод векторних діаграм, записати рівняння результуючого коливання і побудувати графік в залежності від часу.задача 22910
Крапка бере участь одночасно у двох гармонійних коливаннях одного напрямку: X1 = 3 Cos 10,4πt, см; Х2 = 3 Cos 10πt, см. Записати рівняння результуючого коливання. Визначити період биття, період коливання та кількість коливань точки за один період биття. Вкажіть значення max та min амплітуди результуючого коливання.задача 23133
Матеріальна точка бере участь у двох коливаннях, виражених рівняннями х1 = 3 cos t, см, х2 = 3 cos (t + π/3), см. Написати рівняння результуючого коливання.задача 23164
Крапка бере участь у двох взаємно перпендикулярних коливаннях x = sin πt і у = 4 sin(πt + π/2). Знайти траєкторію результуючого руху та накреслити її з дотриманням масштабу.задача 23452
Складаються три гармонійні коливання одного напрямку з однаковими періодами Т1 = Т2 = Т3 = 2 с та амплітудами А1 = А2 = А3 = 3 см. Початкові фази коливань φ1 = 0, φ2 = π/3, φ3 = 2π/3. Побудувати векторну діаграму складання амплітуд. Визначити амплітуду А та початкову фазу φ результуючого коливання. Записати його рівняння.задача 23456
Визначити амплітуду А та початкову фазу φ0 результуючого коливання, що виникає при додаванні двох коливань однакового напрямку з однаковими періодами: х1 = А1sinωt, х2 = А2sinω(t+τ), де А1 = А2 = 1 см, ω = π с–1, τ = 0,5 с. Написати рівняння результуючого руху. Побудувати з дотриманням масштабу векторну діаграму складання амплітуд.задача 23466
Складаються два гармонійні коливання, що відбуваються в одному напрямку: x1 = 2cos2πt см і x2 = 3cos(2πt+π/3) см. Напишіть рівняння результуючого коливання та побудуйте векторну діаграму складання амплітуд.задача 23613
Матеріальна точка бере участь у двох коливаннях однакового періоду з початковими формами π/6 і π/3. Амплітуди коливань 4 см та 6 см. Знайти амплітуду результуючого коливання, якщо коливання відбудеться в одному напрямку.задача 23627
Складаються два коливання однакового напрямку, виражені рівняннями х1 = А1 cos ω(t + τ1) і x2 = A2 cos ω(t + τ2), где А1 = 1 см , А2 = 2 см, τ1 = 1/6 с, τ2 = 1/2 с, ω = π с–1. Визначити: 1) початкові фази φ1 і φ2 складових коливань; 2) амплітуду А та початкову фазу φ0 результуючого коливання. Написати рівняння результуючого коливання. Зобразити векторну діаграму складання амплітуд.задача 24010
Точка бере участь у двох однаково спрямованих коливаннях: x1 = A1sin ωt і х2 = A2cos ωt, де А1 = 3 см, А2 = 4 см, ω = 2 с–1. Визначити амплітуду А результуючого коливання, його частоту f та початкову фазу φ0. Знайти рівняння цього руху.задача 24191
За даними таблиці знайдіть графічно амплітуду і початкову фазу результуючих коливань, що виникають при складанні двох коливань одного напрямку:x1 = A1cos(ω0t + φ01) і x2 = A2cos(ω0t + φ02).
| А1, см | φ01 | А2, см | φ02 |
| 3 | 0 | 2 | –π/3 |
задача 24526
Складаються два гармонійні коливання однакової частоти та однакового напрямку: х1 = А1cos(ωt+φ1) і х2 = А2cos(ωt+φ2). Накреслити векторну діаграму для моменту часу t = 0. Визначити аналітично амплітуду А та початкову фазу φ результуючого коливання. Побудувати векторну діаграму складання амплітуд. Знайти рівняння результуючого коливання (у тригонометричній формі через косинус). Завдання вирішити для випадку: А1 = 1 см, φ1 = π/3, А2 = 2 см, φ2 = 5π/6.задача 24745
Складаються два гармонійні коливання однакової частоти та однакового напрямку: х1 = А1cos(ωt+φ1), x2 = A2cos(ωt+φ2). Накреслити векторну діаграму для моменту часу t = 0. Визначити аналітично амплітуду А та початкову фазу φ результуючого коливання. Знайти рівняння результуючого коливання (у тригонометричній формі через косинус), якщо А1 = 1 см, φ1 = 2π/3, А2 = 1 см, φ1 = 7π/6.задача 25043
Рух точки можна представити як додавання двох коливань одного напрямку та однакової частоти x1(t)=A1cos(ωt+α1) і x2(t)=A2cos(ωt+α2), де A1=2 см, A2=2 см, α1=0 рад, α2=π/3 рад, ω=0,4π рад/с, t=1 с.а) Побудуйте з дотриманням масштабу векторну діаграму складання коливань;
б) Визначте амплітуду A та початкову фазу α результуючого коливання, запишіть його рівняння;
в) Визначте зміщення точки від положення рівноваги та її швидкість у момент часу t.
задача 25044
Рух точки можна представити як додавання двох коливань одного напрямку та однакової частоти x1(t)=A1cos(ωt+α1) і x2(t)=A2cos(ωt+α2), де A1=3 см, A2=2 см, α1=π/3 рад, α2=0 рад, ω=0,8π рад/с, t=0,5 с. а) Побудуйте з дотриманням масштабу векторну діаграму складання коливань; б) Визначте амплітуду A та початкову фазу α результуючого коливання, запишіть його рівняння; в) Визначте зміщення точки від положення рівноваги та її швидкість у момент часу t.задача 25045
Рух точки можна представити як додавання двох коливань одного напрямку та однакової частоти x1(t)=A1cos(ωt+α1) і x2(t)=A2cos(ωt+α2), де A1=1 см, A2=3 см, α1=0 рад, α2=2π/3 рад, ω=π рад/с, t=1 с.а) Побудуйте з дотриманням масштабу векторну діаграму складання коливань;
б) Визначте амплітуду A та початкову фазу α результуючого коливання, запишіть його рівняння;
в) Визначте зміщення точки від положення рівноваги та її швидкість у момент часу t.
задача 25046
Рух точки можна представити як додавання двох коливань одного напрямку та однакової частоти x1(t)=A1cos(ωt+α1) і x2(t)=A2cos(ωt+α2), де A1=2 см, A2=1 см, α1=π/2 рад, α2=π рад, ω=2π рад/с, t=0,5 с. а) Побудуйте з дотриманням масштабу векторну діаграму складання коливань; б) Визначте амплітуду A та початкову фазу α результуючого коливання, запишіть його рівняння; в) Визначте зміщення точки від положення рівноваги та її швидкість у момент часу t.задача 25047
Рух точки можна представити як додавання двох коливань одного напрямку та однакової частоти x1(t)=A1cos(ωt+α1) і x2(t)=A2cos(ωt+α2), де A1=2 см, A2=2 см, α1=π/6 рад, α2= –π/6 рад, ω=π рад/с, t=1 с. а) Побудуйте з дотриманням масштабу векторну діаграму складання коливань; б) Визначте амплітуду A та початкову фазу α результуючого коливання, запишіть його рівняння; в) Визначте зміщення точки від положення рівноваги та її швидкість у момент часу t.задача 25151
Складаються два гармонійні коливання одного напрямку, що описуються рівняннями х1 = 3cos2πt см і х2 = 3cos(2πt+π/4) см. Визначити для результуючого коливання амплітуду та початкову фазу, записати рівняння результуючого коливання. Подати векторну діаграму складання амплітуд.задача 26110
Складаються два гармонійних коливання одного напрямку, описуваних рівняннями x1 = 3cos(2πt+π/4) см і x2 = 5cos(2πt+π/2) см. Визначити для результуючого коливання амплітуду, початкову фазу. Записати рівняння результуючого коливання.задача 26116
Складаються два гармонійних коливання одного напрямку, описуваних рівняннями x1 = 3cos(πt+π/6) см і x2 = 4cos(πt+π/3), см. Визначити для результуючого коливання амплітуду А, початкову фазу α. Записати рівняння результуючого коливання.задача 26118
Частка бере участь одночасно в трьох гармонійних коливаннях, що відбуваються вздовж одного напрямку за законами: x1 = 6cos(ωt) см, x2 = 4cos(ωt+π/2) см, x3 = 2cos( ωt+π) см. Визначити графічним методом амплітуду і початкову фазу результуючого коливання.задача 26432
У вершинах шестикутника поміщені однакові позитивні заряди 10 нКл кожний. Який негативний заряд треба помістити в центрі шестикутника, щоб результуюча сила, що діє на кожен заряд, була рівна нулю?задача 26545
а) Два однаково спрямованих гармонійних коливання одного періоду з амплітудами 5 см і 7 см складаються в одне гармонійне коливання з амплітудою 9 см. Визначити різницю фаз коливань. б) Найбільша швидкість першого коливання дорівнює 50 см/с. Визначити найбільшу швидкість результуючого коливання.задача 40609
Частка бере участь одночасно в трьох гармонійних коливаннях, що відбуваються вздовж одного напрямку за законами: x1 = 2cos(ωt) см, x2 = 4cos(ωt+π/4) см, x3 = 2cos(ωt+π/2) см. Визначити графічним методом амплітуду і початкову фазу результуючого коливання.задача 40648
За даними рівняннями двох простих гармонійних коливань однакової частоти знайти амплітуду і початкову фазу результуючого коливання у = у1+у2: у1 = sin (2/3 t – π/4) і у2 = sin (2/3 t + 5π/12).задача 40649
За даними рівняннями двох простих гармонійних коливань однакової частоти знайти амплітуду і початкову фазу результуючого коливання у = у1+у2: у1 = 2sin (2t + π/3) і у2 = 3sin (2t – π/3).задача 40650
За даними рівняннями двох простих гармонійних коливань однакової частоти знайти амплітуду і початкову фазу результуючого коливання у = у1+у2: у1 = 2sin t/2 і у2 = 2sin (t/2 + 2π/3).задача 40687
Знайти амплітуду і початкову фазу гармонійного коливання, отриманого від складання двох однаково спрямованих коливань, заданих рівняннями x1 = 4sinπt см і x2 = 3sin(πr + π/2) см. Знайти рівняння результуючого коливання.задача 40692
Складаються два гармонійних коливання одного напрямку з однаковими періодами по 1,5 с і однаковими амплітудами по 2 см. Початкові фази коливань відповідно ? / 3 і ? / 2. Визначити амплітуду і початкову фазу результуючого коливання. Записати його рівняння і побудувати з дотриманням масштабу векторну діаграму складання амплітуд.задача 40699
Точка бере участь у двох коливаннях одного напрямку х1 = A1Cosωt і х2 = A2Cos(ω(t+τ)), де А1 = 4 см, А2 = 3 см, ω = π рад/с, τ = 0,5 с. Виконати малюнок і методом векторних діаграм знайти рівняння результуючих коливань.задача 40708
Точка бере участь у двох коливаннях поперечного напряму х = Acosωt і y = Bsin(ω(t+τ)), де A = 5 см, B = 3 см, τ = 1 с, ω = π рад/с. Знайти рівняння траєкторії y (x) результуючого коливання і побудувати його, вказавши напрямок руху точки вздовж траєкторії.задача 60443
У вершинах квадрата зі стороною 41 см знаходяться однакові однойменні заряди по 61 нКл. Який заряд протилежного знака в нКл необхідно помістити в центрі квадрата, щоб результуюча сила, що діє на кожен заряд, дорівнювала нулю?задача 70169
По двох великих колах кулі, вертикальному і горизонтальному, проходять струми 64 A і 69 А. Знайти кут між напрямком результуючого вектора магнітної індукції в центрі кулі і площиною вертикального витка зі струмом.задачи 24186-24210
За даними таблиці знайдіть графічно амплітуду і початкову фазу результуючих коливань, що виникають при складанні двох коливань одного напрямку:x1 = A1cos(ω0t + φ01) та x2 = A2cos(ω0t + φ02).
Другие предметы