заряджений нескінченна протяжна площину заряд відстань поле знаходить
задача 13024
На відстані 40 см від зарядженої нескінченно протяжної площині з поверхневою щільністю заряду 77 нКл/м2 знаходиться однойменно заряджений нескінченно довгий провідний циліндр діаметром 620 мкм з поверхневою щільністю заряду 47 мкл/м2. Визначити різницю потенціалів між циліндром і площиною.задача 14104
На відстані 8 см від нескінченно протяжної зарядженої з поверхневою щільністю –σ = 2·10–6 Кл/м2 площині проведена паралельно їй нескінченно довга нитка, заряджена з лінійною щільністю +τ = 8·10–7 Кл/м. Обчислити напруженість електричного поля в точці, рівновіддаленій від площини і від нитки.задача 14589
Близько зарядженої нескінченно протяжної площини знаходиться точковий заряд q = 0,66 нКл, що має масу m = 0,1 мг. Заряд переміщається по лінії напруженості поля на відстань Δr = 2 см; при цьому відбувається робота A = 5·10–6 Дж. Чому дорівнює швидкість заряду в кінцевій точці, якщо в початковому положенні її швидкість дорівнювала нулю?задача 15105
З якою силою Fs на одиницю площі відштовхуються дві однойменно заряджені нескінченно протяжні площини? Поверхнева щільність заряду на площинах σ = 0,3 мКл/м2.задача 15433
Уздовж силової лінії електричного поля негативно зарядженої протяжної площини рухається електрон. Знайдіть мінімальну відстань, на яку він може наблизитися до площини, якщо на відстані 5 см від площини кінетична енергія електрона 8 кДж, а поверхнева щільність заряду площини 35,4 Кл/м2.задача 15912
Плоска нескінченно протяжна пластина товщиною d = 4 см несе рівномірно розподілений по об'єму заряд (ρ = 8 нКл/м3). В пластині є сферична порожнина радіуса R = d/2. Визначити по модулю і напрямку, напруженість ЕA електричного поля в точці А, що лежить на прямій, що проходить через центр сфери перпендикулярно площині поверхні пластини.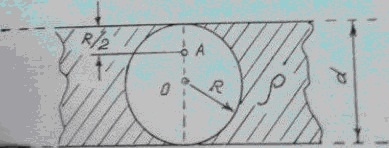
задача 15913
Плоска, нескінченно протяжна пластина, товщиною d = 4 см, несе рівномірно розподілений по об'єму заряд (ρ = 8 нКл/м3). В пластині є циліндрична порожнина радіуса R = d/2. Визначити по модулю і напрямку, напруженість ЕA електричного поля в точці А, що лежить на прямій, перпендикулярній осі циліндра і площині поверхні пластини.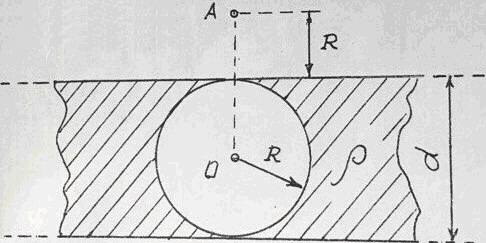
задача 17087
Нескінченно протяжна заряджена з лінійною щільністю τ = 10-7 Кл/м нитка утворює петлю радіуса R = 0,2 м. Визначити напруженість електричного поля в центрі петлі.задача 17342
Методом інтегрування довести, що напруженість електричного поля, створеного нескінченно протяжною рівномірно зарядженою по поверхні пластиною, в будь-якій точці, обчислюється за формулою Е = σ/2ε0.задача 17343
Методом інтегрування визначити напруженість електричного поля, створеного нескінченно протяжною зарядженою по поверхні площиною в точці А, віддаленій від поверхні на відстані S = 0,1 м. (σ = 10–9 Кл/м2).задача 17347
Дві нескінченно протяжні рівномірно заряджені з поверхневою щільністю +σ1 = +σ2 = 10–7 Кл/м2 площині перетинаються під кутом 60 градусів. Знайти величину і напрямок напруженості електричного поля в довільній точці, що лежить на бісектрисі двогранного кута.задача 17351
За межами двох нескінченно протяжних паралельних рівномірно заряджених з поверхневими плотностями +σ1 = 3·10–7 Кл/м2 і –σ2 = 2·10–7 Кл/м2 пластин знаходиться заряд +Q = 4·10–7 Кл. Чому дорівнює сила, що діє на заряд Q?задача 17355
Дві нескінченно протяжні взаємно перпендикулярні площини заряджені з поверхневими густинами σ1 = –4·10–6 Кл/м2 і σ2 = +5·10–6 Кл/м2. Знайти напруженість електричного поля в точці, рівновіддаленій від обох пластин.задача 17359
Знайти поверхневу щільність заряду нескінченно протяжної площини, якщо точковий заряд Q = 10–7 Кл під дією електричного поля переміщується вздовж силової ліній на відстань S = 2 см, при цьому сили поля здійснюють роботу рівну А = 5·10–6 Дж.задача 17366
Дана нескінченно протяжна рівномірно заряджена об'ємною щільністю ρ = 10–5 Кл/м3 пластина товщиною d = 2 см. Знайти різницю потенціалів між двома точками, що лежать уздовж однієї прямої на відстанях а = 4 см і b = 5 см від центру пластини.задача 17368
Електричне поле утворено нескінченно протяжною рівномірно зарядженою з поверхневою щільністю заряду σ = 40·10–9 Кл/м2 площиною. Визначити різницю потенціалів в двох точках, що лежать на перпендикулярі до площини і віддалених від площини на відстанях А = 15 см і В = 20 см.задача 17421
Близько зарядженої нескінченно протяжної площини знаходиться точковий заряд q = 70 нКл. Під дією поля заряд переміщується по силовій лінії на відстань Δr = 2 см, при цьому сили поля здійснюють роботу А = 5 мкДж. Знайти поверхневу щільність заряду на площині.задача 20947
Близько зарядженої нескінченно протяжної площини знаходиться точковий заряд q = 0,66 нКл. Заряд переміщається по лінії напруженості поля на відстань l = 2,0 см. При цьому відбувається робота A = 5,0·10–7 Дж. Знайдіть поверхневу щільність заряду σ на площині.задача 21197
Паралельно до протяжної площини розташована довга нитка. З якою силою буде діяти електричне поле площини на кожен метр довжини нитки, якщо площина заряджена з поверхневою щільністю заряду σ, а нитка — з лінійною щільністю заряду τ?задача 22832
Використовуючи теорему Гаусса, знайдіть напруженість поля, створюваного нескінченно протяжною зарядженою ниткою, як функцію відстані r від нитки. Лінійна щільність заряду нитки дорівнює τ = 5,0 нКл/м. Побудуйте графік залежності Е = f(r).задача 22833
Використовуючи теорему Гаусса, знайдіть напруженість поля, створюваного тонкостінним, нескінченно протяжним, металевим циліндром радіусу R = 5,0 см, як функцію відстані r від осі циліндра. Поверхнева щільність заряду циліндра дорівнює σ = 10 нКл/м2. Побудуйте графік залежності Е = f(r).задача 24505
Використовуючи теорему Гауса, знайдіть напруженість поля, створюваного скляною нескінченно протяжною пластиною завтовшки h = 10 см, як функцію відстані r від центру пластини. Об'ємна щільність заряду пластини дорівнює ρ = 20 нКл/м3. Побудуйте графік залежності Е = f(r). Діелектрична проникність скла ε = 6.задача 24712
Використовуючи теорему Гауса, знайдіть напруженість поля, створюваного суцільним скляним, нескінченно протяжним циліндром радіуса R = 1,0 см, як функцію відстані r від осі циліндра. Об'ємна щільність заряду циліндра дорівнює ρ = 20 нКл/м3. Побудуйте графік залежності Е = f(r). Діелектрична проникність скла ε = 6.задача 24717
Потік вектора напруженості ФЕ, створюваного нескінченно протяжною зарядженою ниткою, через бічну поверхню S циліндра дорівнює 1) ФЕ = 0; 2) ФЕ = E·S·cos90°; 3) ФЕ = E·S·cos0°; 4) ФЕ = E·S·cos180°.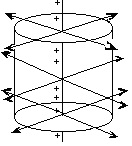
задача 24718
Потік вектора напруженості ФЕ, створюваного нескінченно протяжною зарядженою ниткою, через верхню основу циліндра площею S, дорівнює 1) ФЕ = 0, 2) ФЕ = E·S·cos90°, 3) ФЕ = E·S·cos0°, 4) ФЕ = E·cos0°.
задача 25206
Поверхнева щільність заряду σ нескінченно протяжної вертикальної площини дорівнює 400 мкКл/м2. До площини на нитці підвішено заряджену кульку масою m = 10 г. Визначити заряд Q кульки, якщо нитка утворює з площиною кут φ = 30°.задача 60408
На відстані 20 см від зарядженої нескінченно протяжної площини з поверхневою щільністю заряду 25 нKл/м2 знаходиться однойменно заряджений нескінченно довгий провідний циліндр діаметром 24,8 мкм з поверхневою щільністю заряду 33 мKл/м2. Визначити різницю потенціалів між циліндром і площиною.задача 60611
Поле створюється суцільним скляним нескінченно протяжним циліндром радіуса R = 15 см. Густина його дорівнює 20 нКл/м3. Визначити напруженість поля як функцію відстані від центру циліндра, використовуючи теорему Гаусса. Побудувати графік залежності E = f(r). ε = 7.Другие предметы