точка рухається по траєкторії зі швидкістю напрямок рівняння руху знайти час де
задача 10072
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, рівняння яких х=A1sinω1t і у=А2cosω2t, де A1=8 см, A2=4 см, ω1=ω2=2 с–1. Написати рівняння траєкторії і побудувати її. Показати напрямок руху точки.задача 10573
Матеріальна точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, що відбуваються відповідно до рівнянь: x = A1cos ω1t; y = A2sin ω2t, де A1 = 3 см; ω1 = l с , A2 = 2 см; ω2 = 1 с–1. Визначити траєкторію точки. Побудувати траєкторію з дотриманням масштабу, вказати напрямок руху точки.задача 10576
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, рівняння яких: x = A1 sin ω1t і y = А2 cos ω2t, де А1 = 2 см; A2 = 1 см; ω1 = ω2 = 1 с–1. Написати рівняння траєкторії і побудувати ее на кресленні; показати напрямок руху точки.задача 10578
Точка бере участь у двох взаємно перпендикулярних коливаннях, які висловлюються рівняннями: х = A1cos ω1t і у = A2cos ω2t, де A1 = 2 см; A2 = 3 см; ω1 = 2ω2. Знайти рівняння траєкторії точки і побудувати її на кресленні; показати напрямок руху точки.задача 11014
Рух точки по кривій задано рівняннями x = A1t3 і y = A2t, де A1 = 1 м/с3, A2 = 2 м/с. Знайти рівняння траєкторії точки, її швидкість v і повне прискорення а в момент часу t = 0,8 с.задача 11323
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, які висловлюються рівняннями x = A1cosωt і y = A2sinωt, де A1 = 2 см, A2 = 1 см. Знайти рівняння траєкторії точки і побудувати її, вказавши напрямок руху.задача 11377
Точка здійснює одночасно два коливання, що відбуваються у взаємно перпендикулярних напрямках і виражаються рівняннями x = 8cosπt, y = 8cosπ(t+1) (довжина в сантиметрах, час у секундах). Знайти рівняння траєкторії і побудувати графік її руху.задача 11396
По прямій лінії рухаються дві матеріальні точки відповідно до рівнянь: х1 = 10 + t + 2t2 і x2 = 3 + 2t + 0,2t2. У який момент часу швидкості цих точок однакові?задача 12241
Тіло рухається згідно з рівнянням x = 7 + 4t, t = 2 + 3t. Яка швидкість руху точки?задача 12594
Визначити неточність Δх у визначенні координати електрона, що рухається в атомі водню зі швидкістю v = 1,5·106 м/с, якщо допускаемая неточність Δv у визначенні швидкості складає 10% від її величини. Порівняти отриману неточність з діаметром d атома водню, обчисленим по теорії Бора для основного стану, і вказати, чи можна застосувати поняття траєкторії в даному випадку.задача 12655
Матеріальна точка бере участь одночасно у двох взаємно перпендикулярних коливаннях, рівняння яких в одиницях СІ мають вигляд x = 0,4 cos πt і у = 0,2 cos π(t–0,5). Визначити траєкторію руху точки і накреслити її з дотриманням масштабу. Розрахувати і вказати на кресленні швидкість і прискорення точки у початковий момент часу і вказати напрямок її руху по кривій. Якщо траєкторія не замкнута, то вказати межі руху.задача 12956
Точка рухається по прямій відповідно до рівняння x = At – Bt3 – С, где А = 4 м/с, В = 3 м/с3, С = 1 м. Знайти координати х точки в моменти часу, коли швидкість v дорівнює нулю.задача 13010
З вежі висотою h = 30 м в горизонтальному напрямку кинуто тіло з початковою швидкістю v0 = 10 м/с. Визначте: 1) рівняння траєкторії тіла у(х); 2) швидкість u тіла в момент падіння на Землю; 3) кут φ, який утворює ця швидкість з горизонтом в точці його падіння.задача 13021
Точка рухається в площині xу з положення з координатами х1 = у1 = 0 зі швидкістю v = аi + bхj (a, b - сталі, i, j - орти осей х і у). Визначте: 1) рівняння траєкторії точки у(x); 2) форму траєкторії.задача 13099
Тіло кинуто під кутом α = 45° до горизонту зі швидкістю v0 = 15 м/с Використовуючи закон збереження енергії, визначте швидкість v тіла у вищій точці його траєкторії.задача 14427
З вежі висотою h = 25 м горизонтально кинутий камінь зі швидкістю vx = 15 м/с. Який час t камінь буде в русі? На якій відстані l від основи вежі він впаде на землю? З якою швидкістю v він впаде на землю? Який кут φ складе траєкторія каменю з горизонтом в точці його падіння на землю?задача 14428
Камінь, кинутий горизонтально, впав на землю через час t = 0,5 с на відстані l = 5 м по горизонталі від місця кидання. З якої висоти h кинутий камінь? З якою швидкістю vx він кинутий? З якою швидкістю він впаде на землю? Який кут φ складе траєкторія каменю з горизонтом в точці його падіння на землю?задача 14440
З вежі висотою h0 = 25 м кинутий камінь зі швидкістю v0 = 15 м/с під кутом α = 30° до горизонту. Який час t камінь буде в русі? На якій відстані l від основи вежі він впаде на землю? З якою швидкістю v він впаде на землю? Який кут φ складе траєкторія каменю з горизонтом в точці його падіння на землю?задача 14517
Камінь кинули зі швидкістю v0 = 15 м/с під кутом α = 60° до горизонту. Знайти кінетичну Wк, потенційну Wп і повну W енергії каменю: а) через час t = 1 с після початку руху; б) у вищій точці траєкторії. Маса каменя m = 0,2 кг.задача 14854
Два електрона рухаються в магнітному полі по кругових траєкторіях R1 > R2. Порівняти їх кутові швидкості.задача 14857
Однозарядні іони О+ ізадача 15304
Точка рухається в площині так, що її рух описується рівняннями x = 3t; y = 3t(1+0,5t). Знайти шлях, пройдений матеріальною точкою за 2 секунди; модуль швидкості в цей момент часу. Записати рівняння траєкторії руху матеріальної точки; рівняння радіус вектора; вектора швидкості і вектора прискорення.задача 15531
4 жовтня 1957 в СРСР здійснено запуск першого в світі штучного супутника Землі. Супутник мав форму кулі діаметром 58 см, маса його 83,6 кг; супутник описував еліптичні траєкторії навколо Землі, причому в деякі моменти досягав висоти 900 км над поверхнею Землі. Період обертання супутника навколо Землі виявився рівним 1 годині 36,2 хв. Припустимо, що супутник рухався навколо центру Землі по круговій траєкторії. Якій висоті над поверхнею Землі, якій швидкості і якій кінетичній енергії відповідав би в такому випадку вказаний період обертання?задача 16055
Камінь кинули горизонтально зі швидкістю 15 м/с. Знайти рівняння траєкторії каменю і його повну швидкість через час t = 2 с після кидка.задача 16081
Точка рухається так, що вектор її швидкості V змінюється з часом за законом V = 2i + 2tj + 2t2k (м/с). Знайти модуль переміщення |Δr| за перші 4 с її руху; модуль швидкості в момент часу t = 4 c.задача 16449
Матеріальна точка бере участь одночасно в двох взаємно перпендикулярних коливаннях х = 2 cos t/2, у = –cos t. Визначити рівняння траєкторії і накреслити її з дотриманням масштабу.задача 16566
Точка бере участь в двох взаємно-перпендикулярних коливаннях: х = А1 cos ω1t и у = А1 cos ω2t. Відношення частот коливань, що складаються, 1:2. Знайти рівняння траєкторії точки, побудувати графік і вказати напрямок руху.задача 17200
Рух точки задано рівняннями x = A1sinωt і y = A2sinω(t+τ), де А1 = 10 см, А2 = 5 см, ω = 2 рад/с, τ = π/4 с. Знайти рівняння траєкторії і швидкості точки в момент часу t = 0,5 с.задача 17203
Рух матеріальної точки задано рівнянням x = At + 2Bt2, де А = 0,8 м/с, В = –0,1 м/с2. Обчислити середнє значення модуля швидкості <v> за перші 4 с руху.задача 17496
Матеріальна точка рухається так, що її координати змінюються в залежності від часу відповідно до рівнянь x = A·sin(ω·t); y = A·sin(2ω·t). Запишіть рівняння траєкторії, побудуйте графік у = f(x), визначте швидкість точки через t1 = 1 с, zroj А = 1 см, ω = π рад/c.задача 17510
Залежності координат матеріальної точки по двох взаємно перпендикулярних напрямах описується рівняннями: x(t) = 3sin 3t, y(t) = 6cos 3t, см. Обчисліть: 1) залежність швидкості і прискорення від часу; 2) модулі швидкості і прискорення в момент часу t = 0,2 с; 3) максимальну швидкість точки; 4) рівняння траєкторії руху точки у = f(x); 5) побудуйте графік залежності у = f(х) і визначте координати точок траєкторії, в яких швидкість точки найбільша і найменша. Зобразіть їх на графіку; 6) назвіть характер руху точки.задача 17745
Точка рухається в площині х0у за законом: x = 2sinωt; у = 2cosωt. Знайти шлях, пройдений тілом за 2 с; кут між векторами швидкості v і прискорення a; траєкторію руху y = f(x).задача 17805
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, рівняння яких мають вигляд: Х = 2 Sin ωt, см; Y = Cos 2ωt, см. Знайти рівняння траєкторії руху точки і побудувати траєкторію на кресленні, дотримуючись масштабу. Визначити початкове положення точки і вказати напрямок руху (вектор швидкості) в цей момент часу.задача 17961
Складываются два взаимно перпендикулярных колебания:х = Складаються два взаємно перпендикулярних коливання:
х = 2·cos(ω·t), см;
у = 4·sin(ω·t), см.
Визначити рівняння траєкторії y = f(x), побудувати графік.
задача 18113
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, що виражаються рівняннями х = A1 cos(ωt), y = A2 sin(0,5ωt), де A1 = 2 см, A2 = 3 см. Знайти рівняння траєкторії точки і побудувати її, вказавши напрямок руху.задача 18114
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, що виражаються рівняннями х = A1 cos(ωt), y = A2 sin(0,5ωt), де A1 = 2 см, A2 = 4 см. Знайти рівняння траєкторії точки і побудувати її, вказавши напрямок руху.задача 19691
Точка рухається в площині XY вздовж осі X рівномірно зі швидкістю Vx = 0,5 м/с, а вздовж осі Y так, що рівняння траєкторії має вигляд y = 0,2x2 + 15x3. Знайти залежність швидкості руху точки вздовж осі Y від часу, вважаючи, що при t = 0 точка перебувала на початку координат.задача 19947
Точка бере участь в двох взаємно перпендикулярних коливаннях, які висловлюються рівняннями х = 2 sinωt і у = 3 cosωt. Записати рівняння траєкторії точки і намалювати її траєкторію, показавши напрямок руху точки по траєкторії.задача 19948
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, які висловлюються рівняннями x = 3cosωt і y = –6cosωt. Отримати рівняння траєкторії точки, намалювати її і показати напрямок руху точки.задача 20081
Матеріальна точка бере участь одночасно в двох коливаннях, що відбуваються уздовж взаємно перпендикулярних осей, за законами: x = 0,1sin(2t+π); y = 0,2sin(2t+π), де x і y — відповідні координати точки; t - час в секундах. Знайти рівняння траєкторії результуючого руху, величину і напрямок вектора швидкості в початковий момент часу. Побудувати траєкторію руху (в масштабі).задача 20135
Матеріальна точка має масу m = 9 кг і рухається по криволінійній траєкторії під дією сили, проекція якої на дотичну Fτ = 5,7 Н, на нормаль Fn = 2·t2 Н. Визначте модуль прискорення точки в момент часу t = 19,8 с.задача 20186
Рівняння руху матеріальної точки задається в параметричній формі: x = 4cos3πt, y = 4sin3πt. Побудувати траєкторію руху матеріальної точки і знайти шлях і переміщення за час від t1 = 1 с до t2 = 4 с.задача 20188
Рівняння руху матеріальної точки задається в параметричній формі: x = 4cos3πt, y = 4sin3πt. Побудувати траєкторію руху матеріальної точки і знайти шлях і переміщення за час від t1 = 2 с до t2 = 4 с.задача 20189
Рівняння руху матеріальної точки задається в параметричній формі: x = 2cos2πt, y = 2sin2πt. Побудувати траєкторію руху матеріальної точки і знайти шлях і переміщення за час від t1 = 0,5 с до t2 = 3 с.задача 20387
Від удару футбольний м'яч отримує швидкість 20 м/с під кутом 45° до горизонту. Визначити його швидкість у верхній точці траєкторії, максимальну висоту підйому, час руху і на якій відстані він впаде на Землю?задача 20820
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, що виражаються рівняннями: x = 2sinπt см і y = –cosπt см. Запишіть рівняння траєкторії результуючого руху точки і побудуйте її, вказавши напрямок руху.задача 20825
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, які висловлюються рівняннями: x = 2cosπt см і y = 4sinπt см. Запишіть рівняння траєкторії результуючого руху точки і побудуйте її, вказавши напрямок руху.задача 21392
Точка рухається по прямій відповідно до рівняння х(t) = A cos(ωt). Знайти залежність сили, що діє на точку, від її координати х. Маса точки m. А і ω — сталі.задача 21404
Складаються два взаємно перпендикулярних коливання, які висловлюються рівняннями x = 2sin πt см і у = sin π(t + 0,5) см. Знайти рівняння траєкторії, побудувати графік, показавши напрямок руху точки.задача 21413
Точка рухається по прямій відповідно до рівняння x(t) = 4sin(ωt). Знайти залежність сили, що діє на точку, від її координати х. Маса точки m. А і ω — стала.задача 21909
Точка рухається в площині ху за законом x = αt, у = αt(1–βt), де α і β — позитивні постійні. Знайти: а) рівняння траєкторії точки у(х); зобразити її графік; б) швидкість v і прискорення а точки в залежності від t; у момент t0, коли кут між швидкістю і прискоренням дорівнює π/4.задача 22573
Частка бере участь одночасно в двох взаємно перпендикулярних коливаннях, що описуються рівняннями: х = 2·cos(ωt), см; у = 3·sin(2ωt), см. Запишіть рівняння і побудуйте графік траєкторії частинки, вкажіть напрямок руху частки по ній.задача 22579
Частка бере участь одночасно в двох гармонічних коливаннях, що відбуваються у взаємно перпендикулярних напрямках і описуваних рівняннями х = 4cos(πt), см, у = 8cos(πt + π/2), см. Запишіть рівняння траєкторії руху частинки, побудуйте графік, вкажіть напрямок руху частки по траєкторії.задача 22580
Частка бере участь одночасно в двох гармонічних коливаннях, що відбуваються у взаємно перпендикулярних напрямках і описуваних рівняннями x = 4cos(πt), см, у = 4cos(πt/2 + π/2), см. Запишіть рівняння траєкторії руху частинки, побудуйте графік, вкажіть напрямок руху частки по траєкторії.задача 22687
Матеріальна точка М рухається по колу зі швидкістю V. На рис. 1 показаний графік залежності Vτ від часу (τ — одиничний вектор позитивного спрямування, Vτ — проекція V на цей напрям). На рис. 2 вкажіть напрямок сили, що діє на точку М в момент часу t. Відповідь обґрунтуйте.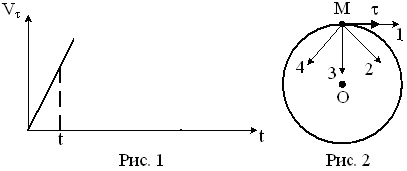
задача 22688
Матеріальна точка М рухається по колу зі швидкістю V. На рис. 1 показаний графік залежності Vτ від часу (τ — одиничний вектор позитивного спрямування, Vτ — проекція V на цей напрям). На рис. 2 вкажіть напрямок сили, що діє на точку М в момент часу t. Відповідь обґрунтуйте.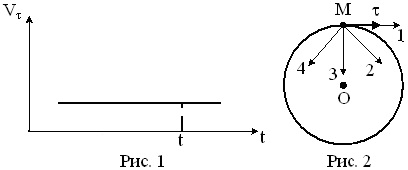
задача 22689
Матеріальна точка М рухається по колу зі швидкістю V. На рис. 1 показаний графік залежності Vτ от времени (τ — одиничний вектор позитивного спрямування, Vτ — проекція V на цей напрям). На рис. 2 вкажіть напрямок сили, що діє на точку М в момент часу t. Відповідь обґрунтуйте.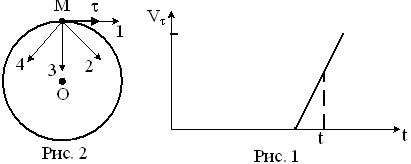
задача 22844
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, які висловлюються рівняннями х = А1 sin ωt і у = А2 cos ωt, де А1 = 2 см, А2 = 1 см. Визначити рівняння траєкторії точки, побудувати траєкторію з дотриманням масштабу. Вказати напрямок руху точки і пояснити свою відповідь.задача 22879
Перша точка рухається траєкторією y = 5x2. Закон руху другої точки: x = 2t (м), y = 8t (м). В який момент часу вони зустрінуться і які координати їхнього місця зустрічі?задача 22881
Тіло рухається з постійною за величиною швидкістю траєкторії, зображеної на малюнку. Для величин повного прискорення тіла у точках А і В справедливе наступне співвідношення … 1) аА < аВ 2) аА > аВ 3) аА = аВ.
задача 23157
Точка рухається в площині хоу за законом: х = –2t; y = 4t(1–t). Знайти рівняння траєкторії у = f(x) та зобразити її графічно; вектор швидкості V та прискорення а залежно від часу; момент часу t0, який вектор прискорення a становить кут π/4 з вектором швидкості V.задача 23224
Рух матеріальної точки в площині задано рівняннями х = A1sin ωt, у = A1sin(ωt+π), де A1 = 2·10–2 м, A2 = 4·10–2 м. Побудувати рівняння траєкторії та накреслити графік.задача 23265
Дано параметричні рівняння руху матеріальної точки: х = 3R·sin(ωt); у = R·cos(ωt). Визначити траєкторію руху точки та її прискорення, якщо R = 10 м, ω = π рад/c.задача 23450
Матеріальна точка бере участь одночасно у двох взаємно перпендикулярних коливаннях, виражених рівняннями х = 1 sinωt см і у = –2 cosωt см. Знайдіть рівняння траєкторії цієї точки та зобразіть її. Визначте напрямок руху цієї точки.задача 23453
Матеріальна точка бере участь у двох взаємно перпендикулярних коливаннях, що виражаються рівняннями х = А1 cos ωt і y = А2 cos 2ωt, де А1 = 2 см, А2 = 1 см. Знайти рівняння траєкторії та побудувати її.задача 23477
Крапка бере участь одночасно у двох взаємно перпендикулярних коливаннях, що описуються рівняннями х = А1cos ωt и у = –А2cos ωt, де А1 = 2 см, А2 = 1 см. Записати рівняння траєкторії точки та побудувати її, вказавши напрямок руху.задача 23971
Тіло рухається траєкторією y = 5x2 – 63x + 5, а його координата х змінюється згідно із законом x = 5t2 (x і y в м, t в с). Знайти момент часу, коли напрямок його швидкості становить 45 градусів з віссю х.задача 24099
Матеріальна точка бере участь у двох взаємно перпендикулярних коливаннях, що виражаються рівняннями x = 3cos(πt), м; y = 2cos[π(t+0,5)], м. Визначити траєкторію точки та накреслити її в масштабі. Вказати напрямок руху точки.задача 24146
Камінь кинутий під кутом α = 30° до горизонту зі швидкістю v0 = 10 м/с (див. рис.). Потрібно: 1) написати кінематичні рівняння руху каменю; 2) вивести рівняння траєкторії каменю; 3) визначити час, через який камінь опиниться на висоті h = 1 м; 4) визначити швидкість v каменю (за модулем і напрямом) на висоті h = 1 м. Камінь розглядати як матеріальну точку та прийняти g = 10 м/с2.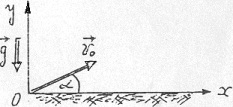
задача 24147
Тіло кинуто під кутом α = 30° до горизонту зі швидкістю v0 = 20 м/с з висоти Н = 10 м. Потрібно: 1) написати кінематичні рівняння руху; 2) вивести рівняння траєкторії; 3) знайти час польоту & # 964; до висоти h = 5 м; 4) визначити по модулю та напрямку швидкість v тіла на висоті h. Тіло розглядати як матеріальну точку та прийняти g = 10 м/с2.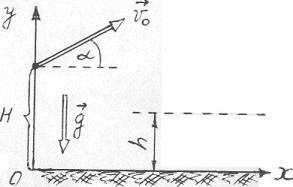
задача 24168
Частка рухається у центральному полі сил із центром у точці О (див. рис.). На малюнку показано ділянку траєкторії. Вважаючи відомими v1, α, r1, β і r2, знайдіть v2.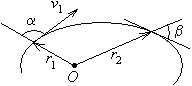
задача 24180
Траєкторія літака, що відображається на екрані радара, є кривою, яку можна описати співвідношеннями x = 1000 + 200·t, y = 2000 – 100·t, z = 5000 + 2·t2 (x, y, z вимірюються за метри, t – за секунди). Знайти швидкість та прискорення літака через 2 сек та через 3 сек після початку спостереження.задача 24539
Пропелер літака радіусом R = 1,5 м обертається із частотою n = 2,1·103 хв–1, посадкова швидкість літака щодо Землі дорівнює v = 161 км/год. Яка швидкість точки на кінці пропелера? Яка траєкторія руху цієї точки?задача 24746
Складаються два взаємно перпендикулярні коливання, що виражаються рівняннями х = А1sinωt и у = А2cosω(t+τ), де А1 = 2 см, А2 = 1 см, ω = π с–1, τ = 0,5 с. Знайти рівняння траєкторії та побудувати її, показавши напрямок руху точки.задача 25048
Точка рухається площиною так, що її координати залежать від часу відповідно до рівнянь x(t)=Acos(ω1t+α1) і y(t)=Bcos(ω2t+α2), де A=3 см, B=2 см, α1=0 рад, α2=π/2 рад, ω1=2π рад/с, ω2=2π рад/с, t=0,25 с.а) Отримайте рівняння траєкторії точки та побудуйте її з дотриманням масштабу; б) Визначте координати точки, її швидкість та прискорення в момент часу t; в) Вкажіть на малюнку положення точки, напрями її швидкості та прискорення у початковий момент часу та в момент часу t.
задача 25049
Точка рухається площиною так, що її координати залежать від часу відповідно до рівнянь x(t)=Acos(ω1t+α1) і y(t)=Bcos(ω2t+α2), де A=2 см, B=2 см, α1=0 рад, α2= –π/2 рад, ω1= 2π рад/с, ω2= 2π рад/с, t=0,25 с.а) Отримайте рівняння траєкторії точки та побудуйте її з дотриманням масштабу; б) Визначте координати точки, її швидкість та прискорення в момент часу t; в) Вкажіть на малюнку положення точки, напрями її швидкості та прискорення у початковий момент часу та в момент часу t.
задача 25050
Точка рухається площиною так, що її координати залежать від часу відповідно до рівнянь x(t)=Acos(ω1t+α1) і y(t)=Bcos(ω2t+α2), де A=1 см, B=2 см, α1=0 рад, α2= 0 рад, ω1=π рад/с, ω2=π рад/с, t=0,5 с.а) Отримайте рівняння траєкторії точки та побудуйте її з дотриманням масштабу; б) Визначте координати точки, її швидкість та прискорення в момент часу t; в) Вкажіть на малюнку положення точки, напрями її швидкості та прискорення у початковий момент часу та в момент часу t.
задача 26241
По прямому шосе зі швидкістю v1 = 16 м/с рухається автобус. На відстані d = 60 м від шосе і s = 400 м від автобуса знаходиться людина. Людина може бігти зі швидкістю v2 = 4 м/с. В якому напрямку він повинен бігти, щоб встигнути "перехопити" автобус? При якій найменшій швидкості людини v2min це взагалі можливо? В якому напрямку необхідно при цьому бігти?задача 26524
Мавпа розгойдувалася на довгій тонкій ліані так, що максимальний кут відхилення ліани від вертикалі склав α. Коли мавпа перебувала в нижній точці траєкторії, ліана зачепилася серединою за гілку дерева. Яким став максимальний кут β відхилення ліани від вертикалі, якщо α < 60°? Що зміниться, якщо 60°< α <90°?задача 26642
Точка рухається по траєкторії згідно рівняння s = 0,5t2+ 4t. Визначити, в який момент часу швидкість точки досягне 10 м/с.задача 40132
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях: х = 2cos(πt/4) і у = 2sin (πt/4). Знайти траєкторію руху точки, побудувати її з дотриманням масштабу.задача 40479
Матеріальна точка рухається під дією сили згідно рівняння Х = A + Вt + Сt2 + Dt3 , де С = 1 м/c2; D = –0,2 м/c3. Визначити, в який момент часу сила дорівнює нулю.задача 40549
Частка рухається в площині xу з точки з координатами x = y = 0 зі швидкістю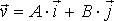
, де А і В — позитивні стал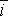і, 
і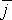 
— орти осей х і у. Знайти рівняння траєкторії частинки.
задача 40563
Тіло кинуто зі швидкістю v0 під кутом α до горизонту. У початковий момент часу t = 0 тіло перебувало в точці з координатами х = у = 0. Знайти рівняння траєкторії руху тіла.задача 40588
Частка рухається згідно рівняння r(t) = А(і cosωt + j sіnωt), де A = 0,5 м, ω = 5 с–1. Зобразіть на малюнку траєкторію руху. Визначте модулі швидкості |v| і модуль нормального прискорення |аn|.задача 40605
Матеріальна точка бере участь одночасно в двох взаємно перпендикулярних гармонійних коливаннях, рівняння яких мають вигляд х = sin(t/2), y = сost. Знайти рівняння траєкторії точки. Побудувати траєкторію з дотриманням масштабу і вказати напрямок руху точки.задача 40617
Ракета пущена під кутом 73 градусів до горизонту з початковою швидкістю 25 м / с. Визначити час горіння запала ракети, якщо відомо, що вона спалахнула в найвищій точці своєї траєкторії.задача 40664
Матеріальна точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, рівняння яких x = 3cos t, y = 2sin t. Знайти траєкторію точки, побудувати її і вказати напрямок руху точки.задача 40666
Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях х = sinπt, y = 4sin(πt + π). Знайти траєкторію руху точки, побудувати її з дотриманням масштабу.задача 40689
Матеріальна точка рухається у відповідності з рівнянням S = 5t + 2t2. Знайти швидкість матеріальної точки через дві секунди після початку руху.задача 40768
Точка одночасно бере участь у двох взаємно перпендикулярних коливаннях, рівняння яких має вигляд x = A1cos(ω1t) і y = A2cos(ω2t), де А1 = 100 мм, А2 = 50,0 мм, ω1 = ω2 = 2,00 с–1. Написати рівняння траєкторії руху точки і побудувати її з дотриманням масштабу. Показати напрямок руху точки.задача 40883
Модель ракети злітає вертикально вгору з прискоренням а = 4 м/с2. Двигун моделі працює протягом 10 с. Обчисліть середню швидкість за час від старту до досягнення найвищої точки траєкторії.задачи 24211-24235
Застосовуючи графічний метод додавання і дотримуючись масштабу, побудуйте траєкторію точки, що світиться, на екрані осцилографа як результат складання двох взаємно перпендикулярних коливань x(t) та y(t), які робить ця точка. Рівняння коливань наведені в таблиці.| задача | Рівняння коливань x(t), y(t) | |
| 24211 | x = A sin ωt, y = A cos 2ωt | Решение на русском языке |
| 24212 | x = A sin 2ωt, y = A sin 3ωt | Решение на русском языке |
| 24213 | x = A cos 3ωt, y = A cos 2ωt | Решение на русском языке |
| 24214 | x = 2A cos ωt, y = A sin 2ωt | Решение на русском языке |
| 24215 | x = 2A cos 3ωt, y = A sin 2ωt | Решение на русском языке |
| 24216 | x = A sin 3ωt, y = A sin ωt | Решение на русском языке |
| 24217 | x = 2A sin ωt, y = A sin 2ωt | Решение на русском языке |
| 24218 | x = 2A cos 2ωt, y = A sin 3ωt | Решение на русском языке |
| 24219 | x = A cos ωt, y = A cos 3ωt | Решение на русском языке |
| 24220 | x = 2A sin 3ωt, y = A cos ωt | Решение на русском языке |
| 24221 | x = A cos 3ωt, y = A sin ωt | Решение на русском языке |
| 24222 | x = 2A cos 2ωt, y = A cos 3ωt | Решение на русском языке |
| 24223 | x = 2A cos 2ωt, y = A sin 2ωt | Решение на русском языке |
| 24224 | x = 2A sin ωt, y = A cos 3ωt | Решение на русском языке |
| 24225 | x = A sin 2ωt, y = A cos 3ωt | Решение на русском языке |
| 24226 | x = 2A cos 2ωt, y = A sin ωt | Решение на русском языке |
| 24227 | x = A cos ωt, y = A sin 3ωt | Решение на русском языке |
| 24228 | x = 2A sin 3ωt, y = A sin 2ωt | Решение на русском языке |
| 24229 | x = A sin 2ωt, y = A cos ωt | Решение на русском языке |
| 24230 | x = 2A sin ωt, y = A sin 3ωt | Решение на русском языке |
| 24231 | x = A cos 2ωt, y = A cos ωt | Решение на русском языке |
| 24232 | x = 2A cos 3ωt, y = A cos ωt | Решение на русском языке |
| 24233 | x = A sin 2ωt, y = A sin ωt | Решение на русском языке |
| 24234 | x = 2A cos ωt, y = A cos 2ωt | Решение на русском языке |
| 24235 | x = 3A sin 3ωt, y = A cos 3ωt | Решение на русском языке |
Другие предметы