логарифмічний декремент загасання коливання раз
задача 11356
Амплітуда коливань маятника довжиною l = 1 м за час t = 10 хв зменшилася в два рази. Визначити логарифмічний декремент коливань θ.задача 11360
Визначити період Т затухаючих коливань, якщо період Т0 власних коливань системи дорівнює 1 с і логарифмічний декремент загасання θ= 0,628.задача 11361
Знайти число N повних коливань системи, протягом яких енергія системи зменшилась у n = 2 рази. Логарифмічний декремент затухання θ = 0,01.задача 11367
Визначити логарифмічний декремент коливань θ коливальної системи, для якої резонанс спостерігається при частоті, меншій власної частоти ν0 = 10 кГц на Δν = 2 Гц.задача 12315
Логарифмічний декремент загасання маятника λ = 0,01. Визначте число повних коливань маятника до зменшення амплітуди в 3 рази.задача 12962
Контур складається з котушки з індуктивністю 2,87·10–2 Гн і опором 11 Ом і конденсатора ємністю 5,15·10–9 Ф. Знайти логарифмічний декремент загасання коливань в контурі.задача 13116
Логарифмічний декремент загасання маятниказадача 13235
Пружинний маятник масою 100 г здійснює затухаючі коливання на пружині жорсткістю k = 6 Н/м. Через якийсь проміжок часу його енергія зменшиться в 16 разів, якщо логарифмічний декремент загасання λ = 0,03? Розрахуйте коефіцієнт загасання β.задача 13693
Період затухаючих коливань T = 1 с, логарифмічний декремент загасання Θ = 0,3, початкова фаза дорівнює нулю. Зсув точки при t = 2Т становить 5 см. Запишіть рівняння руху цього коливання.задача 13699
Тіло масою m = 0,6 кг, підвішене до спіральної пружини жорсткістю k = 30 Н / м, здійснює в деякім середовищі пружні коливання. Логарифмічний декремент коливань Θ = 0,01. Визначте: 1) час, за який амплітуда коливань зменшиться в 3 рази; 2) число повних коливань, які повинна зробити гиря, щоб відбулося подібне зменшення амплітуди.задача 13708
Визначте логарифмічний декремент, при якому енергія коливального контуру за N = 5 повних коливань зменшується у n = 8 разів.задача 13715
Визначте резонансну частоту коливальної системи, якщо власна частота коливань v0 = 300 Гц, а логарифмічний декремент Θ = 0,2.задача 13786
Логарифмічний декремент загасання камертона, що коливається з частотою 100 Гц, дорівнює 0,002. Визначити проміжок часу, за який амплітуда збудженого камертона зменшиться в 50 разів.задача 13844
Логарифмічний декремент коливань маятника 0,02. Визначити, у скільки разів зменшиться амплітуда коливань після 100 повних коливань маятника.задача 14920
Після 100 коливань амплітуда коливань зменшилася в 2,72 рази. Чому дорівнює логарифмічний декремент цього затухаючого коливання?задача 14921
Знайти логарифмічний декремент загасання коливань маятника, якщо за 100 коливань їх амплітуда зменшується в 7,4 рази.задача 14923
Визначити логарифмічний декремент загасання коливальної системи, для якої резонанс спостерігається при частоті, меншій власної частоти 100 кГц на 4 Гц.задача 15084
Знайти логарифмічний декремент загасань λ математичного маятника, якщо за час t = l хв амплітуда коливань зменшилася в 2 рази. Довжина маятника l = 1 м.задача 15511
Період затухаючих коливань T = 4 с; логарифмічний декремент загасання Θ = 1,6; початкова фаза φ = 0. При t = T/4 зміщення точки х = 4,5 см. Написати рівняння руху цього коливання. Побудувати графік цього коливання в межах двох періодів.задача 15514
Логарифмічний декремент загасання математичного маятника χ = 0,2. У скільки разів зменшиться амплітуда коливань за одне повне коливання маятника?задача 15584
Коливальний контур складається з конденсатора ємністю С = 0,2 мкФ і котушки з індуктивністю L = 5,07 мГн. При якому логарифмічному декременті загасання λ різницю потенціалів на обкладинках конденсатора за час t = 1 мс зменшиться в три рази? Який при цьому опір R контуру?задача 16082
Амплітуда коливань математичного маятника довжиною 0,6 м зменшилася в два рази за 10 хв. Визначити логарифмічний декремент загасання і коефіцієнт опору, якщо m = 0,5 г.задача 16083
Амплітуда коливань математичного маятника довжиною 2 м зменшилася в два рази за 10 хвилин. Визначити логарифмічний декремент загасання.задача 16401
Рівняння згасаючих коливань матеріальної точки має вигляд x = 0,01e–3tcos(ωt+π/4), м. Логарифмічний декремент загасання коливань λ = 0,02. Знайдіть частоту ω згасаючих коливань.задача 16467
Коливальний контур складається з конденсатора ємністю С = 10 мкФ, котушки індуктивності L = 0,23 Гн і опори R = 40 Ом. Конденсатору наданий заряд q = 5,6·10–4 Кл. Обчислити період коливання контуру Т і логарифмічний декремент загасання λ.задача 16562
Затухаючі коливання відбуваються в коливальному контурі з ємністю конденсатора 2 мкФ, індуктивністю котушки 350 мГн і опором 15,2 Ом. У початковий момент часу напруга на обкладинках конденсатора була 25 В, а струм в контурі був відсутній. Запишіть рівняння затухаючих коливань для заряду і визначте всі параметри цього рівняння. Визначте логарифмічний декремент загасання.задача 17217
Математичний маятник довжиною l = 24,7 см здійснює затухаючі коливання. Через якийсь час t енергія коливань маятника зменшиться 9,4 рази. Значення логарифмічного декремента загасання θ = 0,01.задача 17218
Математичний маятник довжиною l = 24,7 см здійснює затухаючі коливання. Логарифмічний декремент загасання θ = 3. Визначити час τ, протягом якого енергія W маятника зменшиться в N = 9,4 рази.задача 17373
Рівняння згасаючих коливань матеріальної точки має вигляд x = 0,02e–4t cos(ωt+π/3), м. Якщо логарифмічний декремент загасання коливань λ = 0,1, то чому дорівнює період T згасаючих коливань?задача 17503
За 100 с система встигає зробити 100 коливань. За той же час амплітуда коливань зменшується в 2,718 разів. Чому рівні:а) коефіцієнт загасання коливань β,
б) логарифмічний декремент загасання λ,
в) добротність системи Q,
г) відносний спад енергії системи — Δ
задача 17626
Амплітуда згасаючих коливань математичного маятника за 1 хв зменшується вдвічі. У скільки разів вона зменшиться за 3 хв? Чому дорівнює час релаксації і логарифмічний декремент загасання, якщо довжина маятника 1 м?задача 17829
Пружину жорсткістю k = 0,6 кН/м з грузиком масою m = 0,5 кг на кінці розтягнули на l = 5 см і відпустили. Запишіть рівняння коливань грузика на пружині, якщо він знаходиться в середовищі з коефіцієнтом опору r = 0,9 кг / с. Через який час амплітуда коливань зменшиться в n = 4 раз? Визначте логарифмічний декремент загасання коливань.задача 17869
Визначити координату x матеріальної точки відносно положення рівноваги в момент часу t = 1,3 с, якщо відомо, що амплітуда згасаючих коливань А0 = 20 см, логарифмічний декремент загасання дорівнює 7,564, початкове відхилення x0 = 0, циклічна частота власних коливань ω0 = 1,26 с–1.задача 17918
Коливальний контур складається з конденсатора ємністю С = 0,2 мкФ, котушки індуктивності з L = 10–3 Гн і активного опору. При якому логарифмічному декременті різниця потенціалів на обкладках конденсатора через Δt = 10–3 с від початку коливань зменшиться в 3 рази? Визначити опір контуру.задача 17922
Коливання в контурі описуються рівнянням: q(t) = 0,5e–0,1tcos(104πt), мкКл. Визначити: а) період згасаючих коливань; б) логарифмічний декремент загасання; в) добротність контуру. Записати диференціальне рівняння коливань з числовими коефіцієнтами.задача 18187
Нижче наведені рівняння затухаючих електромагнітних коливань. Логарифмічний декремент загасання найбільший в разі 1) U = 2е–4t cos πt, В 2) q = 0,02е–t cos 4πt, мкКл 3) q = 2e–t cos 2πt, мкКл 4) U = 5e–2t cos(2πt + π), В.задача 19130
Рівняння згасаючих електромагнітних коливань має вигляд: q = q0·e–βtcosωt, q0 = 10–2 Кл, β = 4 c–1, ω = 4π рад/с.Чи вірно, що …
1…. це коливання гармонійне?
2…. амплітуда коливань дорівнює q0 = 10–2 Кл?
3…. час релаксації r = 0,25с?
4…. логарифмічний декремент загасання χ = 2?
На скільки питань і які саме Ви відповіли "так, вірно"?
задача 19165
Знайти коефіцієнт загасання β і логарифмічний декремент загасання χ математичного маятника, якщо відомо, що за час t = 100 с коливань повна механічна енергія маятника зменшилася в десять разів. Довжина маятника l = 0,98 м.задача 19166
Знайти коефіцієнт загасання і логарифмічний декремент загасання математичного маятника, якщо відомо, що за час t = 50 с коливань повна механічна енергія маятника зменшилася в десять разів. Довжина маятника L = 0,98 м.задача 19317
Коливальний контур складається з конденсатора ємністю 0,2 мкФ і котушки індуктивності 5 мГн. При якому логарифмічному декременті загасання різниця потенціалів на обкладках конденсатора за 0,001с зменшиться в три рази? Чому дорівнює опір контуру.задача 19319
Коливальний контур складається з конденсатора з ємністю 0,20 мкФ і котушки індуктивністю 5,5 мГн. При якому логарифмічному декременті загасання різниця потенціалів на обкладках конденсатора зменшиться в три рази через 1,0 мс? Визначте опір контуру при даних умовах.задача 19320
Коливальний контур складається з конденсатора ємністю 0,20 мкФ і котушки індуктивністю 7,5 мГн. При якому логарифмічному декременті загасання різниця потенціалів на обкладках конденсатора за час 5,0 мс зменшиться в три рази? Який при цьому активний опір контуру?задача 19951
Період затухаючих коливань, що здійснюються пружинним маятником, дорівнює T = 4 с, а логарифмічний декремент загасання λ = 0,5. Час, за який амплітуда коливань зменшиться в 3 рази дорівнює (в секундах) ...задача 20233
Коливальний контур містить котушку індуктивністю 5 мГн, конденсатор ємністю 0,4 мкФ і резистор опором 5 Ом. Конденсатор заряджений зарядом 12 мКл. Визначте період коливань контуру, логарифмічний декремент загасання, рівняння залежності зміни струму в котушці від часу.задача 20330
Пружинний маятник відхилили від положення рівноваги на 3 см і відпустили. Після цього за 10 секунд маятник здійснив 20 коливань і амплітуда коливань зменшилася до 1 см. Який логарифмічний декремент коливань цього маятника?задача 20333
Математичний маятник відхилили від положення рівноваги на 3 см і відпустили. Після цього за 10 секунд маятник здійснив 20 коливань і амплітуда коливань зменшилася до 1 см. Який логарифмічний декремент коливань цього маятника?задача 20336
Фізичний маятник відхилили від положення рівноваги на 3 см і відпустили. Після цього за 10 секунд маятник здійснив 20 коливань і амплітуда коливань зменшилася до 1 см. Який логарифмічний декремент коливань цього маятника?задача 20339
Телеграфний стовп відхилили від положення рівноваги на 3 см і відпустили. Після цього за 10 секунд маятник здійснив 20 коливань і амплітуда коливань зменшилася до 1 см. Який логарифмічний декремент коливань цього маятника?задача 20342
Перекриття відхилили від положення рівноваги на 3 см і відпустили. Після цього за 10 секунд маятник здійснив 20 коливань і амплітуда коливань зменшилася до 1 см. Який логарифмічний декремент коливань цього маятника?задача 20492
Тіло масою m = 1 кг знаходиться в в'язкому середовищі з коефіцієнтом опору k = 50 Н/м кожне тіло утримується в положенні рівноваги, пружини при цьому не деформовані (рис. 6.10). Тіло змістили від положення рівноваги і відпустили. Визначити: 1) коефіцієнт загасання δ; 2) частоту ν коливань; 3) логарифмічний декремент коливань Q; 4) число N коливань, по закінченні яких амплітуда зменшиться в е раз.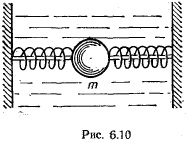
задача 20907
У коливальному контурі з опором R = 50 Ом час релаксації дорівнює 10 мс. Максимальна енергія конденсатора Wmax = 10–3 Дж при амплітудному значенні напруги 5 В. Знайти період коливань і логарифмічний декремент загасання.задача 21122
Рівняння згасаючих коливань для заряду на обкладинках конденсатора має вигляд: q(t) = 4exp(–100t)cos(104πt), мкКл. Ємність конденсатора 10–7 Ф. Визначити: а) індуктивність котушки; б) активний опір контуру; в) логарифмічний декремент загасання.задача 21986
У початковий момент часу зміщення коливної точки максимальне і дорівнює 0,1 м. За 10 коливань амплітуда зменшується на 1/10 своєї початкової величини. Період коливань дорівнює 0,4 с. Визначити коефіцієнт загасання і логарифмічний декремент. Написати рівняння коливань.задача 22077
Знайти логарифмічний декремент коливань θ системи, для якої резонанс спостерігається при частоті, меншій власної частоти ν0 = 10 кГц на Δν = 2 Гц.задача 22223
Контур складається з ємності С = 0,1 мкФ, індуктивності L = 4 мГн і омічного опору. Затухаючі коливання в такому контурі відбуваються за законом: q1 = е–0,1t·cos(5·104πt), мкКл. Визначити: а) період згасаючих коливань; б) опір контуру; в) логарифмічний декремент загасання; г) зміну енергії за період.задача 22427
Математичний маятник довжиною 0,5 м, виведений з положення рівноваги, відхилився при першому коливанні на 5 см, а при другому (в ту ж сторону) на 4 см. Знайти час релаксації, декремент загасання і логарифмічний декремент загасання.задача 22496
У послідовному коливальному контурі відбуваються вільні затухаючі коливання. У момент часу, коли напруга на конденсаторі дорівнювала нулю, амплітуда коливань напруги на конденсаторі була 9,91 В. Коли найближчим часом після цього напруга на конденсаторі знову звернулося до нуля, амплітуда стала 6,44 В. Розрахувати логарифмічний декремент загасання.задача 22504
Пружину жорсткістю k = 0,2 кН/м з грузиком масою m на кінці розтягнули на λ = 6 см і відпустили. Запишіть рівняння коливань грузика на пружині, якщо він знаходиться в середовищі з коефіцієнтом опору r = 0,4 кг/с. Через якийсь час амплітуда коливань зменшиться в n = 2 раз? Визначте логарифмічний декремент загасання коливань.задача 22562
Яким повинен бути логарифмічний декремент загасання маятника, щоб амплітуда зміщення зменшилася в 8 разів за 200 коливань?задача 23298
Визначити, через скільки повних коливань енергія коливального контуру зменшиться у 16 разів, якщо логарифмічний декремент згасання λ = 0,138.задача 23363
Рівняння загасаючих коливань має вигляд x = 0,5е–0,25t sin 0,5πt (м, с). Знайти час релаксації, логарифмічний декремент згасання і швидкість точки, що коливається, в момент часу 0, Т, 2Т (де Т — період коливання).задача 23364
Логарифмічний декремент згасання математичного маятника дорівнює 0,2. Знайти, у скільки разів зменшиться амплітуда коливань за два повні коливання. Напишіть рівняння руху цього маятника, якщо період коливань 2 с, початкова амплітуда 10 см, початкова фаза π/2.задача 23365
Чому дорівнює логарифмічний декремент та коефіцієнт загасання математичного маятника завдовжки 1 м, якщо за 1 хв амплітуда коливань маятника зменшилася вдвічі?задача 23366
Математичний маятник довжиною 24,7 см, здійснює загасаючі коливання. Через скільки часу енергія коливань зменшиться у 9,4 рази? Завдання вирішити за значенням логарифмічного декремента: 1) 0,01 і 2) 0,1.задача 23367
Амплітуда загасаючих коливань маятника за час t1 = 5 хв зменшується вдвічі. За який час t2, рахуючи від початкового моменту, амплітуда зменшиться у вісім разів? З яким логарифмічним декрементом згасання коливається цей маятник, якщо частота його коливань 0,5 с–1?задача 23369
Кулька масою 200 г підвішена на пружині і здійснює вертикальні затухаючі коливання у воді з логарифмічним декрементом 0,05. При цьому за 23 секунди його енергія зменшується в 10 разів. Знайти за цими даними жорсткість пружини.задача 23370
За t = 4 хвилини коливань математичного маятника завдовжки 0,5 м, амплітуда зменшилась у 1,5 раза. Визначте коефіцієнт загасання та логарифмічний декремент λ.задача 23371
Математичний маятник завдовжки l = 1 метр здійснює коливання з логарифмічним декрементом згасання λ = 0,23. Скільки разів зменшиться амплітуда через 10 секунд коливань. Розрахуйте коефіцієнт загасання β.задача 23416
Знайти час t, протягом якого енергія коливань камертону із частотою ν = 440 Гц зменшиться в n = 105 раз, якщо логарифмічний декремент згасання λ = 10–3.задача 23458
Коливальний контур складається з конденсатора ємністю С = 0,2 мкФ та котушки індуктивності L = 5,07 мГн. При якому логарифмічному декременті згасання λ різниця потенціалів на обкладках конденсатора за час t = 1 мс зменшиться вдвічі? Яким є при цьому опір R контуру?задача 23461
Логарифмічний декремент згасання коливань у контурі дорівнює λ = 0,003. Визначити число повних коливань N, протягм яких амплітуда заряду на обкладках конденсатора зменшилася вдвічі.задача 24009
Чому дорівнює логарифмічний декремент згасання математичного маятника, якщо за 1 хв амплітуда коливань зменшилася втричі? Довжина маятника 1м.задача 24104
Амплітуда загасаючих коливань математичного маятника за час t зменшилася в раз. Довжина маятника l. Чому дорівнює логарифмічний декремент згасання?задача 24238
За час t = 100 с тіло масою m = 5 г встигає зробити 100 коливань. Логарифмічний декремент загасання λ = 0,01. Визначте коефіцієнт опору середовища.задача 24240
Амплітуда затухаючих коливань маятника зменшується в е2 раз за час t = 100 с. При цьому система встигає зробити 1000 коливань. Визначте логарифмічний декремент загасання.задача 24242
Логарифмічний декремент загасання маятника λ = 0,003. Визначте число коливань, яку повинен зробити маятник, щоб його амплітуда зменшилася в два рази.задача 24245
Амплітуда коливань маятника довжиною L = 1 м за час t = 10 хв зменшилася в два рази. Визначте логарифмічний декремент загасання.задача 24247
Визначте період власних коливань системи, якщо період згасаючих коливань цієї системи дорівнює 1 с, а логарифмічний декремент загасання λ = 0,628.задача 24248
Знайдіть число повних коливань системи, протягом яких енергія системи зменшилася в 2 рази, якщо логарифмічний декремент загасання λ = 0,01.задача 24252
Математичний маятник здійснює коливання в середовищі, для якого логарифмічний декремент загасання ? = 1,5. Чому буде дорівнює логарифмічний декремент загасання, якщо коефіцієнт опору середовища зменшити в два рази?задача 24255
Логарифмічний декремент загасання математичного маятника λ = 0,2. У скільки разів зменшиться амплітуда коливань за одне повне коливання маятника?задача 24257
До вертикально висячої пружині підвішують вантаж. При цьому пружина подовжується на ΔL = 9,8 см. Після невеликого впливу вантаж починає здійснювати вертикальні коливання. Чому дорівнює коефіцієнт загасання, якщо логарифмічний декремент загасання коливань λ = 0,06?задача 24258
У скільки разів зменшиться амплітуда через 50 затухаючих коливань, якщо логарифмічний декремент загасання дорівнює 0,02?задача 24259
Енергія коливальної системи в початковий момент дорівнює 2 Дж. На скільки вона зменшиться через два повних коливання, якщо логарифмічний декремент загасання λ = 0,02?задача 25004
Математичний маятник довжиною 1,2 м коливається у середовищі з малим опором. Вважаючи, що опір середовища не впливає на період коливання маятника, знайти коефіцієнт загасання та логарифмічний декремент згасання, якщо за 8 хв амплітуда коливань маятника зменшилася втричі.задача 40769
Початкова амплітуда згасаючих коливань маятника А0 = 200 мм, а після вчинення ним N = 10 повних коливань амплітуда А = 10,0 мм. Визначити логарифмічний декремент коливань λ і коефіцієнт загасання δ, якщо період коливань Т = 5,00 с.задача 70036
Логарифмічний декремент загасання тіла, що коливається з частотою 50 Гц, дорівнює 0,01. Визначити: 1) час, за який амплітуда коливань тіла зменшиться в 20 разів; 2) число повних коливань тіла, щоб відбулося подібне зменшення амплітуди.задача 70168
Контур складається з котушки з індуктивністю 9,63·10–2 Гн і опором 8 Ом і конденсатора ємністю 7,53·10–9 Ф. Знайти логарифмічний декремент загасання коливань в контурі.Другие предметы