ймовірний потенційний електрон визначити функція
задача 10455
Хвильова функція, що описує рух електрона в основному стані атома водню, має вигляд ψ(r) = Ae–r/a0, де А — деяка постійна; а0 — перший борівський радіус. Знайти для основного стану атома водню найбільш ймовірну відстань електрона від ядра.задача 10916
Частка в потенційному ящику шириною l знаходиться в збудженому стані (n = 2). Визначити, в яких точках інтервалу (0<x<l) щільність ймовірності знаходження частинки має максимальне і мінімальне значення.задача 10917
Електрон знаходиться в потенційному ящику шириною l. У яких точках в інтервалі (0<x<l) щільність ймовірності знаходження електрона на першому і другому енергетичному рівні однакова? Обчислити значення щільності ймовірності для цих точок. Рішення пояснити графіком.задача 10918
Частка в потенційному ящику знаходиться в основному стані. Яка ймовірність w виявити частинку в середній третині ящика?задача 11163
Частка в потенційному ящику знаходиться в основному стані. Яка ймовірність виявлення частки в інтервалі l/4<x<l/2?задача 11215
Частинка масою 1·10–9 кг знаходиться в потенційній ямі шириною а. Знайти ймовірність виявлення частки в другому збудженому стані у третій чверті ями.задача 12693
Електрон в атомі водню описується в основному стані хвильовою функцією ψ(r) = Се–r/a. Визначити ставлення ймовірностей w1/w2 перебування електрона в сферичних шарах товщиною Δr = 0,01а і радіусами r1 = 0,5а і r2 = 1,5a.задача 12697
Хвильова функція, що описує 2s - стан електрона в атомі водню, має вигляд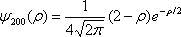
, де ρ — відстань електрона від ядра, виражене в атомних одиницях. Визначити: 1) відстань ρ1 від ядра, на яких ймовірність виявити електрон має максимум; 2) відстані ρ2 від ядра, на яких ймовірність знаходження електрона дорівнює нулю; 3) побудувати графіки залежності [ψ200 (ρ)]2 від ρ і ρ2 [ψ200(ρ)]2 від ρ.
задача 14120
Запишіть вираз для ймовірності W виявлення частки в кінцевому об'ємі V, якщо відома координатна пси-функція частинки ψ(x,y,z).задача 14121
Хвильова функція, що описує деяку частку, може бути представлена у вигляді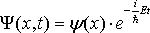
. Покажіть, що щільність ймовірності знаходження частинки визначається тільки координатною ψ-функцією.
задача 14140
Електрон знаходиться в одновимірній прямокутній потенційній ямі шириноюзадача 14261
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частинки Wn = 18,43 эВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність Р(x1, х2) виявлення частки в інтервалі від x1 = 0,3l до x2 = 0,4l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на збудованій залежності знайдену ймовірність.задача 14293
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частинки Wn = 73,72. 1) Знайти квантове число n, що характеризує енергетичний стан частинки. 2) Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від х1 = 0,2l до х2 = 0,3l. 3) Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14306
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частинки Wn = 51,19 еВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від x1 = 0,2l до x2 = 0,3l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14364
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частинки Wn = 2,048 эВ. Найти квантовое число п, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, x2) виявлення частки в інтервалі від x1 = 0,3l до х2 = 0,4l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14365
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частинки Wn = 2,048 эВ. Найти квантовое число п, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, x2) виявлення частки в інтервалі від x1 = 0,4l до х2 = 0,5l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14369
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частинки Wn = 37,68эВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність Р(х1, х2) виявлення частки в інтервалі від x1 = 0,1l до х2 = 0,2l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14381
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частинки Wn = 37,63 эВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність Р(x1, х2) виявлення частки в інтервалі від x1 = 0,2l до х2 = 0,3l. Побудувати графік залежності від координати х щільності ймовірності |ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14384
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частинки Wn = 601,7 эВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність Р(х1, х2) виявлення частки в інтервалі від x1 = 0,1l до х2 = 0,2l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14527
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частинки Wn = 1354 эВ. 1) Знайти квантове число n, що характеризує енергетичний стан частинки. 2) Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від х1 = 0,1l до х2 = 0,2l. 3) Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14580
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частинки Wn = 73,72 эВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність Р(x1, x2) виявлення частки в інтервалі від x1 = 0,3l до x2 = 0,4l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 14621
Частка знаходиться в збудженому стані (n = 4) в потенційному ящику шириною l. Яка ймовірність знаходження частинки в межах 0<x<l/5? Рішення пояснити графічно.задача 16405
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частинки Wn = 338,5 еВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність Р(х1, х2) виявлення частки в інтервалі від х1 = 0,1l до х2 = 0,2l. Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на збудованій залежності знайдену ймовірність.задача 16542
Частка електрон з енергією En = 1354 еВ знаходиться в одновимірній прямокутній нескінченній потенційній ямі шириною l. Знайти головне квантове число n і обчислити вірогідність виявлення частки Р(х) в інтервалі від 0,7l до 0,8l. Побудувати графік залежності хвильової функції Ψn(x) і щільності ймовірності |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність. Маса електрона mе = 9,1·10–31 кг, ширина потенційної ями l = 10–10 м.задача 16604
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 18,43 эВ. Знайти квантове число n, характеризує енергетичний стан частки. Обчислити ймовірність Р(x1, х2) виявлення частки в інтервалі від x1 = 0,4l до x2 = 0,5l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16605
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 73,72. 1) Знайти квантове число n, характеризує енергетичний стан частки. 2) Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від х1 = 0,4l до х2 = 0,5l. 3) Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16607
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частки Wn = 150,4 еВ. 1) Знайти квантове число n, що характеризує енергетичний стан частки. 2) Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від х1 = 0,1l до х2 = 0,2l. 3) Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16608
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частки Wn = 150,4 еВ. 1) Знайти квантове число n, що характеризує енергетичний стан частки. 2) Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від х1 = 0,2l до х2 = 0,3l. 3) Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16609
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частки Wn = 940,2 эВ. Знайти квантове число n, характеризує енергетичний стан частки. Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від x1 = 0,1l до x2 = 0,2l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16610
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 32,76 эВ. Знайти квантове число n, характеризує енергетичний стан частки. Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від x1 = 0,2l до x2 = 0,3l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16611
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 32,76 эВ. Знайти квантове число n, характеризує енергетичний стан частки. Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від x1 = 0,3l до x2 = 0,4l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16612
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 32,76 эВ. Знайти квантове число n, характеризує енергетичний стан частки. Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від x1 = 0,4l до x2 = 0,5l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16613
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частки Wn = 8,191 эВ. Знайти квантове число п, характеризує енергетичний стан частки. Обчислити ймовірність Р(х1, x2) виявлення частки в інтервалі від x1 = 0,3l до х2 = 0,4l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16614
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 8,191 эВ. Знайти квантове число п, характеризує енергетичний стан частки. Обчислити ймовірність Р(х1, x2) виявлення частки в інтервалі від x1 = 0,4l до х2 = 0,5l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16615
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 51,19 эВ. Знайти квантове число n, характеризує енергетичний стан частки. Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від x1 = 0,4l до x2 = 0,5l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16616
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 61,19 эВ. Знайти квантове число n, характеризує енергетичний стан частки. Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від x1 = 0,3l до x2 = 0,4l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16618
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частки Wn = 51,19 эВ. Знайти квантове число n, характеризує енергетичний стан частки. Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від x1 = 0,3l до x2 = 0,4l. Побудувати графік залежності від координати х щільності ймовірності |Ψn(x)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16620
Частка електрон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Енергія частки Wn = 338,5 еВ. 1) Знайти квантове число n, що характеризує енергетичний стан частки. 2) Обчислити ймовірність P(х1, х2) виявлення частки в інтервалі від х1 = 0,2l до х2 = 0,3l. 3) Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16621
Частка електрон з енергією En = 338,4 еВ знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Знайти головне квантове число n і обчислити вірогідність виявлення частки P (x) в інтервалі від х1 = 0,5l до х2 = 0,6l. Побудувати графік залежності хвильової функції Ψn(x) и плотности вероятности |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність.задача 16622
Частка протон з енергією En = 51,19 еВ знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Знайти головне квантове число n і обчислити вірогідність виявлення частки P (x) в інтервалі від х1 = 0,2l до х2 = 0,4l. Побудувати графік залежності хвильової функції Ψn(x) и плотности вероятности |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність.задача 16623
Частка протон з енергією En = 32,76 еВ знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Знайти головне квантове число n і обчислити вірогідність виявлення частки P (x) в інтервалі від х1 = 0,2l до х2 = 0,3l. Побудувати графік залежності хвильової функції Ψn(x) и плотности вероятности |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність.задача 16624
Частка протон з енергією En = 8,191 еВ знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Знайти головне квантове число n і обчислити вірогідність виявлення частки P (x) в інтервалі від х1 = 0,4l до х2 = 0,6l. Побудувати графік залежності хвильової функції Ψn(x) и плотности вероятности |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність.задача 16625
Частка електрон з енергією En = 940,2 еВ знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Знайти головне квантове число n і обчислити вірогідність виявлення частки P (x) в інтервалі від х1 = 0,2l до х2 = 0,5l. Побудувати графік залежності хвильової функції Ψn(x) и плотности вероятности |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність.задача 16626
Частка протон з енергією En = 18,43 еВ знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Знайти головне квантове число n і обчислити вірогідність виявлення частки P (x) в інтервалі від х1 = 0,4l до х2 = 0,5l. Побудувати графік залежності хвильової функції Ψn(x) и плотности вероятности |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність.задача 16627
Частка електрон з енергією En = 150,4 еВ знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–10 м. Знайти головне квантове число n і обчислити вірогідність виявлення частки P (x) в інтервалі від х1 = 0,1l до х2 = 0,3l. Побудувати графік залежності хвильової функції Ψn(x) и плотности вероятности |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність.задача 16628
Частка протон з енергією En = 2,048 еВ знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Знайти головне квантове число n і обчислити вірогідність виявлення частки P (x) в інтервалі від х1 = 0,6l до х2 = 0,9l. Побудувати графік залежності хвильової функції Ψn(x) и плотности вероятности |Ψn(x)|2 виявлення частки в потенційній ямі від координати x. Вказати на графіку знайдену ймовірність.задача 16693
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частинки Wn = 18,43 эВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність Р(х1,х2) виявлення частки в інтервалі від х1 = 0,3l до х2 = 0,4l. Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 16695
Частка протон знаходиться в одновимірній прямокутній безмежно глибокій ямі шириною l = 10–11 м. Енергія частинки Wn = 8,191 эВ. Знайти квантове число n, що характеризує енергетичний стан частинки. Обчислити ймовірність Р(х1,х2) виявлення частки в інтервалі від х1 = 0,3l до х2 = 0,4l. Побудувати залежність від координати х щільності ймовірності |Ψn(х)|2 виявлення частки. Показати на побудованій залежності знайдену ймовірність.задача 17133
Потік електронів, прискорений напругою 199,5 еВ, рухається на бар'єр, який має форму прямокутної сходинки. Висота першої частини сходинки 199,8 еВ при її ширині 0,4 нм; другої — 199,4 еВ. Повна ширина бар'єру 0,6 нм. Визначити ймовірність проникнення електронів за бар'єр.задача 17244
Електрон в одновимірній прямокутній потенційній ямі шириною l = 1 нм з нескінченно високими стінками знаходиться в збудженому стані з n = 4. Визначити: 1) енергію електрона; 2) ймовірність виявлення електрона в першій чверті ями. Пояснити фізичний зміст отриманого результату, зобразивши графічно щільність ймовірності виявлення частки в даному стані.задача 17251
Хвильова функція ψ(x) =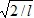
sin(πx/l) описує основний стан частинки в нескінченно глибокій прямокутній потенційній ямі шириною l. Обчислити ймовірність знаходження частинки в малому інтервалі Δl = 0,01l в середній частині ями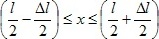 
задача 17567
Протон з енергією 5 еВ рухається в позитивному напрямку осі х, зустрічаючи на своєму шляху прямокутний потенційний бар'єр висотою 10 еВ і шириною 0,1 нм. Визначте ймовірність проходження протоном цього бар'єру. У скільки разів треба звузити бар'єр, щоб ймовірність проходження його протоном була такою ж, як для електрона при вищенаведених умовах.задача 17687
Частка в потенційному ящику шириною l знаходиться в нижчому збудженому стані. Визначити ймовірність знаходження частинки в інтервалі l/4, рівновіддаленому від стінок ящика.задача 18066
Частка знаходиться в потенційному ящику шириною L. Обчислити ймовірність того, що частка перебуває на відстані 1/4 від краю ящика з точністю 0,08L, якщо енергія частки відповідає другому рівню.задача 18068
Частка знаходиться в потенційному ящику. Обчислити ймовірність знайти частинку в першому збудженому стані в першій третині ящика.задача 20224
Частка у потенційній ямі шириною l знаходиться в збудженому стані. Визначити ймовірність знаходження частинки в інтервалі 0 < х < l/4 на другому енергетичному рівні.задача 20225
Частка у потенційній ямі шириною l знаходиться в збудженому стані. Визначити ймовірність знаходження частинки в інтервалі 0 < х < l/2 на третьому енергетичному рівні.задача 21057
Частка в потенційній ямі шириною l знаходиться в збудженому стані. Визначити ймовірність знаходження частинки в інтервалі 0 < x < l/4 на другому енергетичному рівні.задача 21377
Електрон знаходиться в одновимірній прямокутній ''потенційній ямі" шириною l з нескінченно високими "стінками". Визначте ймовірність W виявлення електрона в середній третині "ями", якщо електрон знаходиться в збудженому стані (n = 3). Поясніть фізичний зміст отриманого результату, зобразивши графічно щільність ймовірності виявлення електрона в даному стані.задача 22831
Електрон в атомі водню описується в основному стані хвильовою функцією Ψ(r) = Се–r/a. Визначити відношення ймовірностей w1/w2 перебування електрона в сферичних шарах товщиною Δr = 0,01а і радіусами r1 = 0,75а і r2 = 1,25а.задача 23012
Вважаючи, що поглинений квант з ймовірністю 0,5 породжує пару електрон-дірка, визначте кількість пар, що генеруються, за наступних умов: сила джерела світла 160 канделл, фотоопір знаходиться на відстані 0,5 м від джерела, довжина хвилі дорівнює 500 нм і площа фотоопору 10 см2.задача 23729
У скільки разів відрізняються ймовірності заповнення електронами станів з енергією на 5,2·10–2 еВ вище і нижче значення хімічного потенціалу при Т = 300 К?задача 23841
Прямокутний потенційний бар'єр має ширину 0,1 нм. За якої різниці U–Е ймовірність проходження електрона через бар'єр дорівнює 0,99?задача 23843
Яка можливість визначити електрон на нижньому рівні зони провідності у власному германії, якщо температура зразка дорівнює: а) 30 К; б) 300 К.задача 24005
Частка знаходиться в нескінченно глибокій прямокутній потенційній скриньці, шириною l. Стан часток характеризується хвильовим числом k = π/l. Яка ймовірність W виявити частинку в області 0 ≤ x ≤ l/4? Зобразіть на графіку та заштрихуйте площу, що відповідає знайденому значенню ймовірності.задача 90130
Визначте ймовірність знаходження електрона в потенційній ямі шириною l для найнижчого енергетичного стану в області з координатами l/3≤x≤2/3l.задача 90140
Частка у потенційній ямі шириною l знаходиться в нижчому збудженому стані. Визначити ймовірність знаходження частинки в інтервалі l/2, рівновіддаленому від стінок ями.Другие предметы