знайти декартові координати точки
задача 13111
Провести аналіз окремих газових процесів (ділянки 1-2, 2-3, і т.д.). Зобразити процеси у координатах p (V) і р(Т).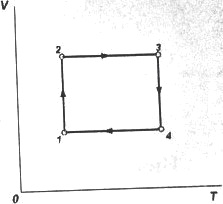
задача 17726
Матеріальна точка масою 0,2 кг рухається зі стану спокою з прискоренням a = 0,8ti + 0,9t2j – k, м/с2, де вектори i, j, k є ортами декартової системи координат. Яку роботу зробила рівнодіюча сила за другу секунду руху?задача 17727
Матеріальна точка масою 0,2 кг рухається зі стану спокою з прискоренням a = 6ti –3t2j, м/с2, де вектори i, j, k є ортами декартової системи координат. Яку роботу зробила рівнодіюча сила за другу секунду руху?задача 18102
Визначити дивергенцію і ротор векторного поля, що має в декартовій системі координат єдину складову Ах = 20 sin (х/п).задача 18239
Для електромагнітної хвилі з частотою зі діелектрична проникність середовища ε = 2, магнітна проникність середовища μ = 1. Знайти модуль вектора Пойнтінга в точці, де вектор напруженості електричного поля змінюється за законом E = 10cos(ωt + α) ez. Амплітуда напруженості магнітного поля дорівнює H = Н0ex. Тут ex, ey, ez — одиничні орти декартової системи координат.задача 21957
Знайти ротор і дивергенцію наступних векторних полів, заданих в декартовій системі координат: А = cos (ay) lx + sin (ax) ly + tg (az) lz, B = 6xlx + 5zly + 10ylz.задача 25894
Дві матеріальні точки рухаються по одній прямій, що збігається з віссю Ох декартової системи координат. У початковий момент часу перша точка мала координату х10 = 4 м, а друга х20 = 8 м. Швидкості точок змінюються за законами v1 = bt + ct2 і v2 = –bt + ct2, где b = 1 м/с2, с = 2 м/с3. Визначити прискорення точок у момент їхньої зустрічі.задача 23754
Дві матеріальні точки рухаються по одній прямій, що збігається з віссю 0x декартової системи координат. Закон руху першої точки має вигляд х1 = А + Bt + Ct2 + Dt3, а швидкість другої точки змінюється відповідно до рівняння v2x = α + βt + γt2. У початковий момент часу друга точка мала координату х20 = δ.A = 2 м; B = 4 м/с; C = 2 м/с2; D = 1 м/с3; α = 1 м/с; β = 6 м/с2; γ = 0 м/с3; δ = 1 м.
Визначте прискорення першої точки в той момент, коли швидкості точок стануть однаковими.
задача 23777
Дві матеріальні точки рухаються по одній прямій, що збігається з віссю 0x декартової системи координат. Закон руху першої точки має вигляд х1 = А + Bt + Ct2 + Dt3, а швидкість другої точки змінюється відповідно до рівняння v2x = α + βt + γt2. У початковий момент часу друга точка мала координату х20 = δ.A = 6 м; B = 2 м/с; C = –3 м/с2; D = 1 м/с3; α = 2 м/с; β = 4 м/с2; γ = 9 м/с3; δ = 5 м.
Визначте відстань між точками в той момент, коли прискорення першої точки дорівнюватиме нулю.
Другие предметы