обід радіусом обертається з прискоренням момент точка швидкість колеса знайти час
задача 10047
Визначити момент сили М, який необхідно прикласти до блоку, що обертається з частотою n = 12 с–1, щоб він зупинився протягом часу Δt = 8 с. Діаметр блоку D = 30 см. Масу блоку m = 6 кг вважати рівномірно розподіленим по ободу.задача 12544
Диск радіусом R = 5 см обертається навколо нерухомої осі так, що залежність кутової швидкості від часу задається рівнянням ω = 2At + 5Bt4 (A = 2 рад/с2, В = 1 рад/с5). Визначити для точок на ободі диска до кінця першої секунди після початку руху: 1) повне прискорення; 2) число оборотів, зроблених диском.задача 12870
Рівняння обертання колеса радіусом R = 0,5 м має вигляд φ = At + Bt5, де А = 2 рад/с; В = 0,5 рад/с5. Визначити повне прискорення в момент t = 1 с точки, що знаходиться на ободі колеса.задача 12938
Залежність кута повороту радіуса обертового колеса від часу представлена рівнянням φ = 4+10t-3t3. Знайти в кінці першої секунди обертання кутову швидкість колеса, а також лінійну швидкість і повне прискорення точки на ободі колеса. Радіус колеса 2 см.задача 13017
Точка А знаходиться на ободі колеса радіусом 69 см, яке котиться без ковзання по горизонтальній поверхні зі швидкістю 5 м/с. Знайти повний шлях, що проходить точка A між двома послідовними моментами її торкання поверхні.задача 13137
До ободу однорідного суцільного диска радіусом R = 0,5 м прикладена постійна дотична сила F = 100 Н. При обертанні диска на нього діє момент сил тертя Mтр = 2 Н·м. Визначте масу m диска, якщо відомо, що його кутове прискорення ε постійно і дорівнює 16 рад/с².задача 13306
Лінійна швидкість v1 точки, яка знаходиться на ободі диска, що обертається, в три рази більше, ніж лінійна швидкість v2 точки, яка знаходиться на 6 см ближче до його осі. Визначте радіус диска.задача 13319
Диск обертається навколо нерухомої осі так, що залежність кута повороту радіуса диска від часу задається рівнянням φ = At2 (А = 0,1 рад/с2). Визначте повне прискорення а точки на ободі диска на кінець другої секунди після початку руху, якщо лінійна швидкість тієї точки в цей момент дорівнює 0,4 м/с.задача 13320
Диск радіусом R = 10 см обертається так, що залежність лінійної швидкості точок, що лежать на ободі диска, від часу задається рівнянням v = At+Bt2 (А = 0,3 м/с2, B = 0,1 м/с3). Визначте кут α, який утворює вектор повного прискорення а з радіусом колеса через 2 с від початку руху.задача 13321
Диск радіусом R = 10 см обертається так, що залежність лінійної швидкості точок, які лежать на ободі диска, від часу задається рівнянням v = At+Bt2 (А = 0,3 м/с2, B = 0,1 м/с3). Визначте момент часу, для якого вектор повного прискорення а утворює з радіусом колеса кут φ = 4°.задача 13592
На обід маховика діаметром D = 30 см намотаний шнур, до кінця якого прив'язаний вантаж масою m = 2 кг. Тертя в підшипниках створює постійний момент Мтр = 0,1 Н·м. Яку швидкість матиме вантаж, спустившись з висоти h = 2 м? Маса маховика М = 20 кг.задача 13842
До обіду диска масою 5 кг прикладена дотична сила 19,6 Н. Яку кінетичну енергію буде мати диск через 5 секунд після початку дії сили?задача 13933
До обода колеса, яке має форму диска радіусом 0,5 м і масою 50 кг, прикладена дотична сила 98 Н. Знайти: 1) кутове прискорення колеса; 2) через який час після початку дії сили колесо матиме швидкість, що відповідає 100 об/с?задача 14167
Залежність кута повороту радіуса обертового колеса від часу дана рівнянням: φ = 4 + 5t – t2. Знайти кутову і лінійну швидкість обертання колеса, а також повне прискорення точки, що лежить на ободі колеса в кінці першої секунди обертання. Радіус колеса 20 см.задача 14168
Залежність кута повороту радіуса обертового колеса від часу дана рівнянням: φ = 4 + 5t2 – t3. Знайти в кінці першої секунди обертання кутову швидкість колеса, а також лінійну швидкість і повне прискорення точки, що лежить на ободі колеса радіусом 20 см.задача 14169
Залежність кута повороту радіуса обертового колеса від часу дана рівнянням: φ = 4t + 5t2 – t3. Знайти в кінці другої секунди обертання кутову швидкість колеса, а також лінійну швидкість і повне прискорення точки, що лежить на ободі колеса. Радіус колеса 2 см.задача 14446
Знайти радіус R обертового колеса, якщо відомо, що лінійна швидкість v1 точки, що лежить на ободі, в 2,5 рази більше лінійної швидкості v2 точки, що лежить на відстані r = 5 см ближче до осі колеса.задача 14459
Знайти кутове прискорення ε колеса, якщо відомо, що через час t = 2 с після початку руху вектор повного прискорення точки, що лежить на ободі, становить кут α = 60° з вектором її лінійної швидкості.задача 14462
Колесо радіусом R = 5 см обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct2 + Dt 3, де D = 1 рад/с3. Для точок, що лежать на ободі колеса, знайти зміна тангенціального прискорення Δaτ за одиницю часу.задача 14463
Колесо радіусом R = 5 см обертається так, що залежність лінійної швидкості точок, що лежать на ободі колеса, від часу дається рівнянням v = At + Bt2, де А = 3 см/с2 і В = 1 см/с3. Знайти кут α, що складається вектором повного прискорення з радіусом колеса в моменти часу t, рівні: 0, 1, 2, 3, 4 і 5 с після початку руху.задача 14464
Колесо обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням φ = А + Bt + Ct2 + Dt3, де В = 1 рад/с, С = 1 рад/с2 і D = 1 рад/с3. Знайти радіус R колеса, якщо відомо, що до кінця другого секунди руху для точок, що лежать на ободі колеса, нормальне прискорення аn = 3,46·102 м/с2.задача 14629
До ободу однорідного диска радіусом R = 0,2 м прикладена дотична сила F = 98,1 Н. При обертанні на диск діє момент сил тертя Mтр = 9,81 Н·м. Знайти масу m диска, якщо відомо, що диск обертається з кутовим прискоренням ε = 100 рад/с2.задача 14641
Колесо складається з обода масою 10 кг, діаметром 1 м і шести спиць, маса кожної з яких дорівнює 1 кг. Визначити момент інерції колеса відносно осі, що проходить через центр колеса перпендикулярно його площині.задача 14642
Однорідний диск масою 3 кг і радіусом 20 см, що обертається з кутовою швидкістю 16π рад/с, починає гальмуватися дотичною силою 0,05 Н, прикладеною до його обода. Скільки обертів зробить диск до зупинки?задача 14659
По ободу шківа, насадженого на загальну вісь з маховим колесом, намотана нитка, до кінця якої підвішений вантаж масою m = 1 кг. На яку відстань h повинен опуститися вантаж, щоб колесо зі шківом отримало швидкість, відповідну частоті колеса n = 60 об/хв? Момент інерції колеса зі шківом J = 0,42 кг·м2, радіус шківа R = 10 см.задача 15133
Визначити повне прискорення в момент часу 3 с точки, що знаходиться на ободі колеса радіусом 0,5 м, що обертається згідно рівняння: φ = At + Bt3, де А = 2 с–1, В = 0,2 с–2, φ — кут повороту радіуса колеса. Вважаючи, що обертання колеса відбувається в горизонтальній площині, зобразити вектори швидкостей і прискорень (лінійних і кутових), в зазначений вище момент часу.задача 15419
До ободу однорідного диска радіусом r = 0,2 м прикладена постійна дотична сила F = 100 Н. При обертанні на диск діє сила тертя, момент якої М = 5 Н·м. Диск обертається з постійним кутовим прискоренням α = 100 рад·с–2. Визначити масу диска.задача 15452
Тіло починає рух зі стану спокою і обертається з постійним кутовим прискоренням ε = 0,04 с–2. Через скільки часу точка, що належить цьому тілу, матиме прискорення, спрямоване під кутом 45° до його швидкості?задача 16059
До ободу однорідного диска радіусом 0,2 м прикладена дотична сила 10 Н. Знайти масу диска, якщо відомо, що диск обертається з кутовим прискоренням 10 рад/с2.задача 16129
Маховик масою 4 кг вільно обертається навколо горизонтальної осі, що проходить через його центр, роблячи 720 об/хв. Масу маховика можна вважати розподіленою по його ободу радіусом 40 см. Через 30 с під дією гальмуючого моменту маховик зупинився. Знайти гальмуючий момент і число оборотів, яке робить маховик до повної зупинки.задача 16131
Визначити період коливань переднього колеса велосипеда, піднятого в вертикальне положення. Колесо складається з обода, масу якого m1 = 3 кг можна вважати рівномірно розподіленим по колу з радіусом R = 35 см і з укріпленого на ободі вентиля (m2 = 50 г). Моментом інерції спиць і втулки знехтувати.задача 16710
Колесо радіуса R рухається горизонтально зі швидкістю v0 і обертається з кутовою швидкістю ω. Точка А на ободі (рис. 8) описує в просторі деяку траєкторію. Знайти радіус її кривизни ρ в момент, коли точка знаходиться на рівні центру колеса.задача 17985
Шків колеса має горизонтальну вісь. На обід шківа намотаний шнур, до вільного кінця якого підвішена гиря масою m, Вважаючи масу шківа рівномірно розподілену по обіду, знайти натяжіння Т шнура при русі вантажу. Тертям і масою шнура знехтувати.задача 18961
Однорідний диск радіуса 0,10 м і маси 5,0 кг обертається навколо своєї осі з кутовою швидкістю ω = A +Bt, де В = 8 рад/с2. Знайдіть величину дотичної сили, прикладеної до обода диска, вважаючи її постійною.задача 18962
Диск радіуса 20 см і маси 2 кг обертається навколо своєї осі з кутовою швидкістю ω = 20+8t (рад/с). Знайдіть дотичну силу, прикладену до обода диска.задача 19141
До ободу однорідного диска радіусом 0,2 м прикладена постійно дотична сила 100 Н. При обертанні на диск діє сила тертя, момент якої 5 Н·м. Обчисліть масу диска, якщо відомо, що він обертається з постійним кутовим прискоренням 100 рад/с2, а також кінетичну енергію в момент часу 1 с.задача 19144
До ободу однорідної кулі радіусом 0,1 м прикладена постійно дотична сила 50 Н. При обертанні на кулю діє сила тертя, момент якої 4 Н·м. Обчисліть масу кулі, якщо відомо, що вона обертається з постійним кутовим прискоренням 80 рад/с2, а також його кінетичну енергію в початковий момент часу.задача 19176
До ободу однорідного циліндра радіусом 0,3 м прикладена постійно дотична сила 150 Н. При обертанні на диск діє сила тертя, момент якої 6 Н·м. Обчисліть масу тіла, якщо відомо, що воно обертається з постійним кутовим прискоренням 150 рад/с2, а також його кінетичну енергію в момент часу 1 с.задача 19609
Диск радіусом R = 10 см обертається так, що залежність лінійної швидкості точок, що лежать на ободі диска, від часу задається рівнянням v = At + Bt2 (A = 0,3 м/с2, В = 0,1 м/с3). Визначте момент часу, для якого вектор повного прискорення a утворює з радіусом колеса кут φ = 4°.задача 19898
До ободу однорідного диска радіусом 0,2 м прикладена постійна дотична сила 98,1 Н. При обертанні на диск діє момент сил тертязадача 19907
Дан графік залежності кутової швидкості від часу для обруча, що обертається в горизонтальній площині щодо вертикальної осі, яка проходить через одну з точок на його ободі. Побудувати графік залежності моменту сили, що діє на обруч, від часу. Момент інерції обруча дорівнює 20 кг·м2.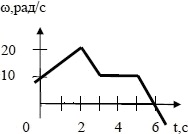
задача 20068
Залежність кута повороту радіуса (r = 2 м) обертового колеса від часу задана рівнянням φ = 4+5t–t3. Знайти кутову швидкість і повне прискорення точки, що лежить на ободі колеса, в кінці першої секунди обертання. Які середні швидкість і прискорення за цей час?задача 20163
Однорідний диск масою m і радіусом R починає обертатися навколо нерухомої осі, що проходить через центр диска перпендикулярно його площині, під дією дотичної сили, яка додається до обода диска. Модуль сили залежить від часу як F = αt2, де α — деяка позитивна постійна. Знайти кутову швидкість ω1 диска в момент часу t1 після початку дії сили.задача 20264
Знайти радіус R обертового колеса, якщо відомо, що лінійна швидкість точки v1, що лежить на його ободі, в n = 2,5 разb більше лінійної швидкості точки v2, що лежить на δх = 6,0 см ближче до осі колеса.задача 20665
Маховик радіусом 1 м обертається за законом φ = t3 – 3t2, рад. Визначити нормальне прискорення точки, що знаходиться на ободі маховика в момент часу, коли дотичне прискорення точки звертається в нуль.задача 20734
Колесо радіусом R = 10 см обертається так, що залежність кута повороту радіуса колеса від часу задана рівнянням φ = 3+2t2+t3, где φ — в радіанах, t — в секундах. Знайдіть для точок, що лежать на ободі колеса: а) лінійну швидкість, б) нормальне прискорення і в) кутове прискорення ε для моменту часу t = 3 с.задача 21361
До обіду однорідного диска радіусом 29 см прикладена постійна дотична сила 63 Н. При обертанні на диск діє момент сил тертя 2 Н·м. Знайти масу диска, якщо він обертається з постійним кутовим прискоренням 70 рад/с.задача 21388
До обіду диска радіусом R = 5 см прикладена дотична сила F = 19,6 Н. Який момент імпульсу матиме диск через час 5 с після початку дії сили?задача 22920
Два вантажі m1 = 1 кг и m2 = 0,5 кг пов'язані легким шнуром, перекинутим через блок. Блок радіусом R = 10 см обертається із кутовим прискоренням β = 20 рад/с2. Знайти масу блоку, якщо вона рівномірно розподілена за його ободом.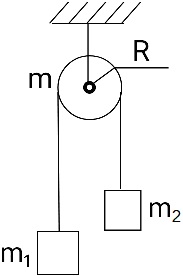
задача 23143
Радіус-вектор матеріальної точки у початковий момент часу r(0) = 2i – 4j + k, швидкість залежить від часу за законом v(t) = 2ti – (4 – t)j + k. Знайти величину переміщення матеріальної точки за час від t = 3 сек до t = 5 сек.задача 23954
Колесо починає обертатися навколо осі з кутовим прискоренням ε = 4 рад/c2. Через який проміжок часу кут між вектором швидкості та вектором прискорення точки на обід колеса стане рівним α = 45°?задача 23986
Час розгону автомобіля до швидкості 130 км/год становить 13 секунд. Які в момент закінчення розгону автомобіля доцентрове, тангенціальне та повне прискорення точок, розташованих на обід колеса при розгоні (щодо автомобіля)? Діаметр колеса рівний 0,5 м.задача 23991
Диск, що знаходився в стані спокою, почав обертатися з постійним кутовим прискоренням ε = 0,25 рад/с2. Через скільки часу кут між векторами швидкості та прискорення становитиме α = 45°?задача 24047
Обруч починає обертатися так, що повне прискорення точок обода а = 2,0 м/с2, а тангенціальне прискорення аτ = const. Чому дорівнює момент сили і момент імпульсу в час, коли швидкість обруча V = 0,6 м/с. Маса обруча m = 0,50 кг, радіус r = 0,25 м. Вісь обертання проходить через центр обруча перпендикулярно до його площини.задача 24263
Колесо радіусом R = 0,1 м обертається так, що залежність кутової швидкості від часу визначається рівнянням ω = 2At + 5Bt4 (А = 2 рад/с2 і В = 1 рад/с5). Визначте повне прискорення точок обода колеса через t = 1 с після початку обертання та кількість обертів, зроблених колесом за цей час.задача 24307
До обода колеса, що має форму диска, радіусом R = 0,5 м і масою m = 50 кг прикладена дотична сила 10 Н. Знайти: 1) кутове прискорення колеса; 2) через скільки часу після початку дії сили колесо матиме швидкість, що відповідає 100 об/с?задача 24797
Колесо обертається згідно із законом φ = 4 + 5t – t3. Знайти лінійну швидкість в кінці другої секунди, повне прискорення точок колеса, що знаходиться на обіді, радіусом 2 см.задача 24903
Диск радіуса R, що обертається навколо своєї осі з кутовою швидкістю ω, кинуто під кутом α до горизонту зі швидкістю v0. Точка A на обід описує в просторі деяку траєкторію (рис. 1.7). Знайти радіус її кривизни ρ у момент найбільшого підйому, якщо точка A знаходиться при цьому над центром колеса.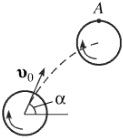
задача 26296
До ободу диска радіусом R = 0,5 м прикладена дотична сила F = 100 Н, що повідомляє йому кутове прискорення ε = 7,8 рад/c2. Визначити масу колеса m і час t, протягом якого колесо набуває швидкість, що відповідає частоті n = 50 об/c.задача 26685
Яку роботу потрібно провести, щоб маховику масою m = 0,6 т, розподіленою по ободу з діаметром D = 1,6 м, надати обертання з частотою n = 240 хв-1?задача 40540
Точка А знаходиться на ободі колеса радіусом 23 см, яке котиться без ковзання по горизонтальній поверхні зі швидкістю 5 м/с. Знайти повний шлях, що проходиться точкою А між двома послідовними моментами її торкання поверхні.задача 40551
Знайти повне прискорення в момент часу t = 3 c точки, яка знаходиться на ободі колеса радіусом R = 0,5 м, що обертається згідно рівняння φ = Аt + Вt3, де А = 2 рад/с, В = 0,2 рад/с3.задача 40606
Диск радіусом R = 10 см обертається так, що залежність лінійної швидкості точок, що лежать на ободі диска, від часу задається рівнянням v = At + Вt2 (А = 0,3 м/с2, В = 0,1 м/с3). Визначити момент часу, для якого вектор повного прискорення a утворює з радіусом колеса кут φ = 45°.задача 40625
Знайти радіус колеса, що обертається, якщо відомо, що лінійна швидкість точки, яка лежить на ободі колеса, в 4 рази більше лінійної швидкості точки, яка знаходиться на 28 см ближче до осі колеса.задача 40626
Лінійна швидкість v1 точки, яка знаходиться на ободі диска, що обертається, в чотири рази більше, ніж лінійна швидкість v2 точки, яка знаходиться на 28 см ближче до його осі. Визначте радіус диска.задача 40642
Маси вантажів, показаних на малюнку, m1 = 1,5 кг, m2 = 2 кг, маса блоку m3 = 1 кг. Коефіцієнт тертя між вантажем m1 і горизонтальною поверхнею столу, по якому цей вантаж рухається, дорівнює μ = 0,2. З яким прискоренням рухаються вантажі?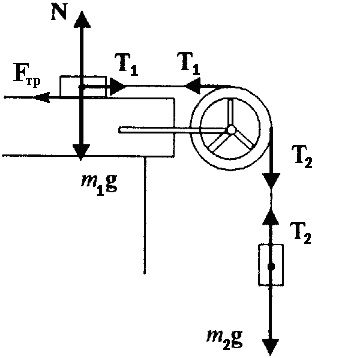
задача 40714
На одному валу насаджені два колеса з різними діаметрами 16 см і 4 см обертаються з постійним кутовим прискоренням, рівним 4 рад/с2. Визначити лінійні швидкості на ободах коліс і кутову швидкість обертання в кінці 2-ої секунди після початку руху.задача 40787
Маховик, масу якого m = 5 кг можна вважати розподіленою по ободу радіуса r = 20 см, вільно обертається навколо горизонтальної осі, що проходить через його центр, з частотою 720 хв–1. При гальмуванні маховик зупиняється через проміжок часу Δt = 20 с. Знайти число обертів N, яке зробить маховик до повної зупинки.задача 40819
Порівняйте кінетичну енергію диска, що обертається навколо нерухомої осі і котиться по горизонтальній площині. Лінійна швидкість точок на ободі диска однакова.задача 40878
У центрі горизонтальної платформи, яка може вільно обертатися навколо вертикальної осі, стоїть людина і тримає велосипедне колесо, що обертається з кутовою швидкістю 10 рад/с. Вісь колеса розташована вертикально і збігається з віссю платформи. З якою швидкістю почне обертатися платформа, якщо колесо повернути навколо горизонтальної осі на 90°? Момент інерції людини і платформи 6 кг·м2, діаметр колеса 70 см, маса обода колеса 6 кг.Другие предметы