точка здійснює гармонійні коливання частотою амплітуда період швидкість
задача 11306
Визначити максимальні значення швидкості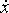
max і прискорення 
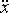max точки, що здійснює гармонічні коливання з амплітудою А = 3 см і кутовий частотою ω = π/2 с–1.
задача 11309
Максимальна швидкість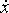max точки, що здійснює гармонічні коливання, дорівнює 10 см/с, максимальне прискорення 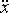max = 100 см/с2. Знайти кутову частоту ω коливань, їх період Т і амплітуду А. Написати рівняння коливань, прийнявши початкову фазу рівною нулю.
задача 11312
Коливання точки відбуваються за законом x = Acos(ωt+φ). У деякий момент часу зміщення х точки дорівнює 5 см, її швидкість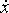 = 20 см/с і прискорення 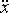= –80 см/с2. Знайти амплітуду A, кутову частоту ω, період Т коливань і фазу (ωt+φ) в даний момент часу.
задача 11998
Напишіть рівняння гармонійного коливання з амплітудою 5 см, якщо за 1 хв відбувається 150 коливань і початкова фаза коливання дорівнює 45°. Накресліть графік цього руху.задача 12625
Написати рівняння гармонійного коливального руху з амплітудою 5 см, якщо у 1 хв відбувається 150 коливань і початкова фаза дорівнює 45°. Вивести для цього випадку залежність швидкості і прискорення від часу.задача 12835
Горизонтально розташована дошка здійснює гармонійні коливання у горизонтальній площині з періодом, рівним 19 с. Тіло, що лежить на ній, починає ковзати, коли амплітуда коливання досягає величини 63 см. Який коефіцієнт тертя спокою між вантажем і дошкою?задача 12976
Горизонтально розташована дошка здійснює гармонійні коливання в горизонтальній площині з періодом, рівним 9 с. Тіло, що лежить на ній, починає ковзати, коли амплітуда коливання досягає величини 74 см. Який коефіцієнт тертя спокою між вантажем і дошкою.задача 13632
Гармонійні коливання величини s описуються рівнянням s = 0,02cos(6πt+π/3), м. Визначте: 1) амплітуду коливань; 2) циклічну частоту; 3) частоту коливань; 4) період коливань.задача 13634
Матеріальна точка здійснює гармонічні коливання з амплітудою А = 4 см і періодом T = 2 с. Напишіть рівняння руху точки, якщо її рух починається з положення х0 = 2 см.задача 13638
Точка здійснює гармонійні коливання з амплітудою А = 10 см і періодом Т = 5 с. Визначте для точки: 1) максимальну швидкість, 2) максимальне прискорення.задача 13642
Визначте максимальні значення швидкості і прискорення точки, що здійснює гармонічні коливання з амплітудою А = 3 см і періодом T = 4 с.задача 13643
Матеріальна точка, яка здійснює гармонічні коливання з частотою v = 1 Гц, в момент часу t = 0 проходить положення, яке визначається координатою x0 = 5 см, зі швидкістю v0 = 15 см/с. Визначте амплітуду коливань.задача 13683
Автомобіль масою 1850 кг при русі по ребристій дорозі здійснює гармонійні коливання у вертикальному напрямку з періодом 0,924 с і амплітудою 18 см. Визначте максимальну силу тиску, що діє на кожну з чотирьох ресор автомобіля.задача 14124
Скласти рівняння гармонійного коливання, якщо амплітуда коливань 5,0 см, а час одного повного коливання 0,50 с.задача 14258
Знайти амплітуду А і початкову фазу φ0 гармонічного коливання, отриманого від складання однаково спрямованих коливань, заданих рівняннями х1 = 0,02sin(5πt + π/2) м і x2 = 0,030sin(5πt + π/4) м.задача 14351
Рівняння гармонійних коливань тіла має вигляд x = 0,1sin π(t/8+1/4), м. Чому рівні амплітуда, частота і початкова фаза коливань?задача 14352
Рівняння гармонійних коливань тіла має вигляд x = 4,2sin(πt/2+π/8), см. Чому рівні період, амплітуда і початкова фаза цих коливань?задача 14353
Рівняння гармонійних коливань тіла має вигляд x = 0,01sin π(t/8+1/2), м. Чому рівні амплітуда, частота і початкова фаза коливань?задача 14354
Рівняння гармонійних коливань тіла має вигляд x = cos 5πt, см. Визначте амплітуду, циклічну частоту, період і початкову фазу цих коливань.задача 14355
Рівняння гармонійних коливань тіла має вигляд x = 4sin π(t+0,1), см. Визначте амплітуду, циклічну частоту, період і початкову фазу.задача 14912
Горизонтально розташована дошка здійснює гармонійні коливання в горизонтальній площині з періодом, рівним 4 с. Тіло, що лежить на ній, починає ковзати, коли амплітуда коливання досягає величини 60 см. Який коефіцієнт тертя спокою між вантажем і дошкою?задача 14913
Горизонтально розташована дошка здійснює гармонійні коливання в горизонтальній площині з періодом, рівним 7 с. Тіло, що лежить на ній, починає ковзати, коли амплітуда коливання досягає величини 32 см. Який коефіцієнт тертя спокою між вантажем і дошкою?задача 14914
Горизонтально розташована дошка здійснює гармонійні коливання в горизонтальній площині з періодом, рівним 18 с. Тіло, що лежить на ній, починає ковзати, коли амплітуда коливання досягає величини 64 см. Який коефіцієнт тертя спокою між вантажем і дошкою?задача 14915
Горизонтально розташована дошка здійснює гармонійні коливання в горизонтальній площині з періодом, рівним 8 с. Тіло, що лежить на ній, починає ковзати, коли амплітуда коливання досягає величини 17 см. Який коефіцієнт тертя спокою між вантажем і дошкою?задача 14917
Горизонтально розташована дошка здійснює гармонійні коливання в горизонтальній площині з періодом, рівним 17 с. Тіло, що лежить на ній, починає ковзати, коли амплітуда коливання досягає величини 80 см. Який коефіцієнт тертя спокою між вантажем і дошкою?задача 14918
Горизонтально розташована дошка здійснює гармонійні коливання в горизонтальній площині з періодом, рівним 16 с. Тіло, що лежить на ній, починає ковзати, коли амплітуда коливання досягає величини 32 см. Який коефіцієнт тертя спокою між вантажем і дошкою?задача 14962
Підставка здійснює в горизонтальному напрямку гармонійні коливання з періодом 5 с. Тіло, що знаходиться на підставці, починає по ній ковзати, коли амплітуда коливань підставки досягає 0,5 м. Визначити коефіцієнт тертя між тілом і підставкою.задача 15101
Точка виконує гармонічні коливання уздовж деякої прямої з періодом Т = 0,60 с і амплітудою а = 10,0 см. Знайти середню швидкість точки за час, протягом якого вона проходить шлях а/2: а) з крайнього положення; б) з положення рівноваги.задача 15722
Тіло здійснює гармонійні коливання. Період коливань Т = 0,15 с, максимальна швидкість v = 8 м/с. Визначити амплітуду коливань.задача 15870
Математичний маятник здійснює гармонійні коливання. У скільки разів зменшиться кутова амплітуда коливання, якщо довжину нитки маятника змінити від 0,5 м до 0,72 м, не змінюючи повної енергії коливань? При малих відхиленнях вважати sin(α)≈α, cos(α)≈1–α2/2.задача 15899
Матеріальна точка масою m = 0,025 кг здійснює гармонійні коливання з частотою ω0 = 1,6 рад/с, маючи при цьому енергію W = 0,2 Дж. Знайти амплітуду коливань.задача 16416
Точечная частица совершает гармонические колебания вдоль оси Оx. В некоторый момент времени частица имеет координату x1 = 3 см, скорость vx1 = 8 см/с и ускорение ax1 = –12 см/с2. Определите амплитуду, циклическую частоту и период колебаний. Начало координат совпадает с положением равновесия частицы.задача 17033
Знайти кругову частоту і амплітуду гармонійних коливань частинки, якщо на відстанях х1 і х2 від положення рівноваги її швидкість дорівнює відповідно v1 і v2.задача 17061
Дошка з лежачим на ній бруском здійснює горизонтальні гармонійні коливання з амплітудою a = 10 см. Знайти коефіцієнт тертя між дошкою і бруском, якщо брусок починає ковзати по дошці, коли її період коливання менше Т = 1,0 c.задача 17110
Амплітуда сигналу від радіомаяка змінюється в приймальнику корабля, що віддаляється, з періодом 5 хв. Визначити швидкість корабля, якщо висота радіомаяка над рівнем моря Н = 250 м, висота щогли корабля, що віддаляється, h = 19,5 м, відстань, на якому реєструється сигнал d = 3,5 км. Довжина хвилі радіовипромінювання 0,4 м.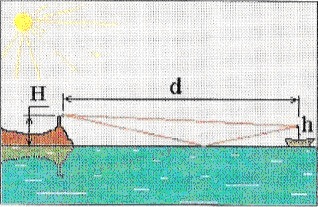
задача 17256
Матеріальна точка масою m = 400 г здійснює гармонійні коливання по горизонтальній осі Ох за законом x = 20sin πt/2 (х виражено в см, t — в с). Знайти силу, що діє на точку в крайніх точках, амплітуду, період і кінетичну енергію в положенні рівноваги.задача 17505
Тіло маси m впало с висоти h на чашку пружинних ваг (рис. 4.9). Маса чашки дорівнює М, маса пружини нехтовно мала, жорсткість останньої k. Прилипнувши до чашки, тіло починає здійснювати гармонічні коливання у вертикальному напрямку. Знайти амплітуду коливань в цьому випадку.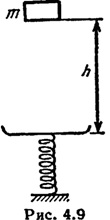
задача 17915
Тіло маси m впало з висоти h на чашку пружинних ваг (рис. 4.9). Маса чашки дорівнює М, маса пружини нехтовно мала, жорсткість останньої k. Прилипнувши до чашки, тіло починає здійснювати гармонічні коливання у вертикальному напрямку. Знайти амплітуду коливань в цьому випадку.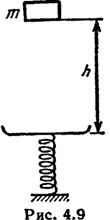
задача 17929
Визначити максимальне прискорення amax матеріальної точки, що здійснює гармонічні коливання з амплітудою A = 15 см, якщо максимальна швидкість точки vmax = 30 см/с. Написати також рівняння коливань.задача 19618
Швидкість звуку в воді 1450 м/с. На якій відстані знаходяться найближчі точки, які вчиняють коливання в протилежних фазах, якщо частота коливань дорівнює 725 Гц?задача 20790
Максимальна швидкість точки, що здійснює гармонічні коливання дорівнює υ = 10 см/с, максимальне прискорення а = 100 см/с2. Знайти кутову частоту ω коливань, їх період T і амплітуду A.задача 20955
Точка підвісу математичного маятника, період власних коливань якого дорівнює Т = 1 с, здійснює синусоїдальні коливання з амплітудою Ап = 1 см і періодом Тп = 1,1 с. Яка амплітуда А сталих коливань маятника?задача 21340
Точка здійснює синусоїдальні вільні коливання. Початкове відхилення дорівнює нулю, початкова швидкість 10 см/с, частота 10 герц. Знайти амплітуду і початкову фазу. Побудувати графік.задача 21341
Точка здійснює синусоїдальні вільні коливання. Початкове відхилення дорівнює 2 см, початкова швидкість 10 см/с, частота 10 герц. Знайти амплітуду і початкову фазу.задача 21662
Амплітуди вимушених гармонічних коливань при частотах 400 і 700 Гц рівні між собою. Знайти (в Гц) резонансну частоту. Загасанням знехтувати.задача 21669
Швидкість звуку в воді 1450 м/с. На якій (в см) відстані знаходяться найближчі точки, які вчиняють коливання в протилежних фазах, якщо частота коливань дорівнює 1 кГц?задача 22003
Максимальне значення швидкості гармонійно коливної матеріальної точки дорівнює 20 см/с. Величина максимального прискорення дорівнює 4,0 м/с2. Визначити кругову частоту і амплітуду коливань. Записати рівняння гармонійних коливань в загальному вигляді, отримати з нього закон коливань швидкості і прискорення.задача 22005
Однорідна куля діаметром 80 см робить коливання навколо горизонтальної осі, що проходить крізь шар на відстані а = 16 см від його центру. Визначити період і циклічну частоту загасаючих коливань. Скласти диференціальне рівняння гармонійних коливань для кутового зміщення кулі, користуючись основним рівнянням динаміки обертального руху (аналог 2-го закону Ньютона) і записати його рішення. Покласти амплітуду коливань φm = 0,085 рад.задача 22130
Швидкість звуку в воді v = 1450 м/с. На якій відстані знаходяться найближчі точки, що здійснюють коливання в протилежних фазах, якщо частота коливань f = 725 Гц?задача 22189
Тіло здійснює гармонійні коливання за законом косинуса з частотою 2 Гц. Початкова фаза дорівнює 15°. Через скільки секунд після початку руху кінетична енергія в перший раз буде рівною потенційній?задача 22387
Тіло масою m = 20 г, яка вчиняє гармонійні коливання з частотою ν = 1 Гц, в момент часу T = 0 проходить положення, яке визначається координатою x0 = 5 см, зі швидкістю v0 = 15 см/с. Визначити в момент часу t = 0,8T, де Т — період коливань, кінетичну енергію тіла Wk і її імпульс Р. Побудувати графіки залежності (в межах одного періоду з числовими значеннями) X(T), v(t), А(t).задача 23475
Точка М одночасно коливається за гармонійним законом вздовж осей координат ОХ та ОУ з різними амплітудами, але однаковими частотами. На якому малюнку траєкторія точки має вигляд, що відповідає різниці фаз 2π? Вкажіть його номер та поясніть відповідь.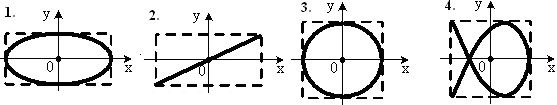
задача 23577
Матеріальна точка робить гармонійні коливання з амплітудою X0 = 0,02 см та частотою ν0 = 500 Гц. Визначити середні та максимальні значення швидкості υ та прискорення а точки при її русі з крайнього становища до положення рівноваги.задача 23814
Амплітуда гармонійних коливань точки А = 5 см, амплітуда швидкості vmax = 7,85 см/с. Обчислити циклічну частоту ω коливань та максимальне прискорення аmax точки.задача 24027
Тіло масою 50 г здійснює гармонійне коливання з амплітудою 4 см та частотою 3 Гц. Чому дорівнює максимальна сила, що повертає, і повна енергія коливань?задача 24028
Амплітуда швидкості матеріальної точки, що здійснює гармонійне коливання, дорівнює 4 см/с, а амплітуда прискорення 16 см/с2. Знайти амплітуду зміщення та циклічну частоту коливань.задача 24029
Під дією вантажу масою 300 г пружина розтягується на 3 см. Вантажу повідомили кінетичну енергію 0,5 Дж і він став здійснювати гармонійне коливання. Визначити частоту та амплітуду коливань.задача 24376
Вантаж масою m = 500 г, підвішений на пружині жорсткістю k = 100 Н/м, здійснює гармонічні коливання з енергією E = 1 Дж. Знайти період коливань, їх амплітуду та максимальну швидкість вантажу.задача 24770
Рівняння гармонійного коливання системи має вигляд х = 4·10–2·е–0,2t sin π/8·t м. Визначити: власну частоту коливань системи; амплітуду після трьох повних коливань.задача 40528
Автомобіль масою 1883 кг при русі по ребристій дорозі здійснює гармонійні коливання у вертикальному напрямку з періодом 0,481 с і амплітудою 24 см. Визначте максимальну силу тиску, що діє на кожну з чотирьох ресор автомобіля.задача 40647
Знайти максимальну кінетичну енергію Тmax матеріальної точки масою m = 2 г, що здійснює гармонічні коливання з амплітудою А = 4 см і частотою ν = 5 Гц.задача 40659
Горизонтальна підставка здійснює вертикальні гармонійні коливання з амплітудою А = 5 мм. При якій частоті коливань ν предмет, що лежить на підставці, не відривається від неї?задача 40663
Визначити максимальне прискорення матеріальної точки, що здійснює гармонійні коливання з амплітудою 15 см, якщо її найбільша швидкість дорівнює 30 см/с. Написати рівняння коливань, якщо початкова фаза дорівнює 60°.задача 40683
Визначити максимальну швидкість матеріальної точки, що здійснює гармонійні коливання з амплітудою А = 20 см, якщо найбільше прискорення amax = 30 см/с2. Написать также уравнение колебаний.задача 60563
Рівняння напруженості електричного поля біжучої електромагнітної гармонійної хвилі має вигляд E = 40sin π(3·1014t+106x) B/м. Знайдіть амплітуду, частоту, період, довжину хвилі і швидкість поширення хвилі.Другие предметы