Заказать решения
Задачи по физике (рус)
Задачі з фізики (укр)
Вопросы по физике:
6 класс Другие предметы
|
температура скорость определить интервал времени
задача 10490
Определить долю свободных электронов в металле при температуре T = 0 К,  и ε которых заключены в интервале значений о и ε которых заключены в интервале значений о 1/2εmax 1/2εmax  о εmax. о εmax.
задача 10505
Точка движется  о прямой согласно уравнению х = At+Bt3, где A = 6 м/с; B = 0,125 м/с3. Определить среднюю скорость <Δs/Δt> точки в интервале времени о о прямой согласно уравнению х = At+Bt3, где A = 6 м/с; B = 0,125 м/с3. Определить среднюю скорость <Δs/Δt> точки в интервале времени о t1 = 2 c t1 = 2 c  о t2 = 6 с. о t2 = 6 с.
задача 11002
Движение точки по прямой задано уравнением x = At+Bt2, где A = 2 м/с, В = -0,5 м/с2. Определить среднюю путевую скорость движения точки в интервале времени от t1 = 1 с до t2 = 3 с.
задача 11035
Велосипедное колесо вращалось с частотой n = 5 с–1. Под действием сил трения оно останавливается через интервал времени Δt = 1 мин. Определите угловое ускорение ε и число N оборотов, которое сделало колесо за это время.
задача 11701
Электрон находится в однородном электрическом поле напряженностью Е = 200 кВ/м. Какой путь пройдет электрон за время t = 1 нс, если его начальная скорость была равна нулю? Какой скоростью будет обладать электрон в конце этого интервала времени?
задача 12469
Определите, какая часть молекул азота при температуре t = 27°С обладает скоростями, модули которых лежат в интервале от 210 до 215 м/с.
задача 12556
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 11 м оно было два раза с интервалом во времени 3 с.
задача 12689
Газообразный азот находится в равновесном состоянии при нормальных условиях. Найти относительное число молекул, имеющих положительные проекции скорости vx в интервалах от 60 до 65 м/с и от 300 до 305 м/с. Объяснить полученный результат.
задача 12702
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 10 м оно было два раза с интервалом во времени 4 с. Сопротивление воздуха не учитывать.
задача 12703
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 11 м оно было два раза с интервалом во времени 4 с. Сопротивление воздуха не учитывать.
задача 12704
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 11 м оно было два раза с интервалом во времени 5 с. Сопротивление воздуха не учитывать.
задача 12705
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 12 м оно было два раза с интервалом во времени 4 с. Сопротивление воздуха не учитывать.
задача 12706
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 14 м оно было два раза с интервалом во времени 3 с. Сопротивление воздуха не учитывать.
задача 12707
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 15 м оно было два раза с интервалом во времени 2 с. Сопротивление воздуха не учитывать.
задача 12708
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 15 м оно было два раза с интервалом во времени 3 с. Сопротивление воздуха не учитывать.
задача 12709
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 15 м оно было два раза с интервалом во времени 4 с. Сопротивление воздуха не учитывать.
задача 12710
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 17 м оно было два раза с интервалом во времени 5 с. Сопротивление воздуха не учитывать.
задача 12711
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 18 м оно было два раза с интервалом во времени 3 с. Сопротивление воздуха не учитывать.
задача 12712
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 19 м оно было два раза с интервалом во времени 4 с. Сопротивление воздуха не учитывать.
задача 12713
Определить начальную скорость, с которой тело брошено вертикально вверх, если на высоте 20 м оно было два раза с интервалом во времени 4 с. Сопротивление воздуха не учитывать.
задача 13011
Зависимость пройденного телом пути о  и задается уравнением s = A−Bt + Ct² + Dt³ (A = 6 м, В = 3 м/с, С = 2 м/с², D = 1 м/с³). Определите для тела в интервале времени о и задается уравнением s = A−Bt + Ct² + Dt³ (A = 6 м, В = 3 м/с, С = 2 м/с², D = 1 м/с³). Определите для тела в интервале времени о t1 = 1 c t1 = 1 c  о t2 = 4 c 1) среднюю скорость, 2) среднее ускорение. о t2 = 4 c 1) среднюю скорость, 2) среднее ускорение.
задача 14102
Определить долю Δ
задача 14230
Температура кислорода 208°С. Определить отношение числа молекул этого газа, модули скоростей которых лежат в интервале 798-802 м/с, к числу молекул, модули скоростей которых лежат в интервале 398-402 м/с.
задача 14231
Температура кислорода 28°С. Определить отношение числа молекул этого газа, модули скоростей которых лежат в интервале 798-802 м/с, к числу молекул, модули скоростей которых лежат в интервале 398-402 м/с.
задача 14232
Температура кислорода 210°С. Определить отношение числа молекул этого газа, модули скоростей которых лежат в интервале 800-804 м/с, к числу молекул, модули скоростей которых лежат в интервале 400-404 м/с.
задача 14245
Найти число ΔN молекул кислорода, занимающего при нормальных условиях объем V = 10 мм3, скорости которых лежат в интервале значений от v1 = 0 до v2 = 0,01vвер. Число Лошмидта nл = 2,69·1019 см–3 считать известным. На графике Nf(v) заштриховать площадь, соответствующую найденному значению Δ
задача 14412
Тело бросили вертикально вверх с начальной скоростью v0 = 9,8 м/с. Постройте график зависимости высоты h и скорости v от времени t для интервала 0 ≤ t ≤ 2 с через 0,2 с.
задача 15312
Два тела брошены вертикально вверх из одной точки друг за другом с интервалом времени t = 5 с и одинаковыми начальными скоростями v0 = 2 м/с. Через какое время t1 отсчитываемое от момента бросания первого тела, тела встретятся?
задача 15312
Тело брошено под углом 30° к горизонту. С какой скоростью было брошено тело и какова горизонтальная дальность его полета, если оно находилось в полете 2 с? Какова максимальная высота подъема тела? Сопротивлением воздуха пренебречь.
задача 15930
Уравнение движения точки имеет вид x = –270+12t. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 20 c, Δt = 2,0 c); 6) указать характер движения точки.
задача 15931
Уравнение движения точки имеет вид x = –1,5t. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 10 c, Δt = 1,0 c); 6) указать характер движения точки.
задача 15932
Уравнение движения точки имеет вид x = 2+0,4t2. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 40 c, Δt = 4,0 c); 6) указать характер движения точки.
задача 15933
Уравнение движения точки имеет вид x = 1–0,2t2. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 30 c, Δt = 3,0 c); 6) указать характер движения точки.
задача 15934
Уравнение движения точки имеет вид x = –0,4t2. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 20 c, Δt = 2,0 c); 6) указать характер движения точки.
задача 15935
Уравнение движения точки имеет вид x = 2+5t. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 50 c, Δt = 5,0 c); 6) указать характер движения точки.
задача 15936
Уравнение движения точки имеет вид x = 150–10t. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 40 c, Δt = 4,0 c); 6) указать характер движения точки.
задача 15937
Уравнение движения точки имеет вид x = 400–0,6t. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 100 c, Δt = 10,0 c); 6) указать характер движения точки.
задача 15938
Уравнение движения точки имеет вид x = 10t+0,4t2. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 20 c, Δt = 2,0 c); 6) указать характер движения точки.
задача 15939
Уравнение движения точки имеет вид x = 2t–t2. По уравнению определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 15 c, Δt = 1,5 c); 6) указать характер движения точки.
задача 20454
Найти для газообразного азота при Т = 300 К отношение числа молекул с компонентами скорости вдоль оси х в интервале 300±0,31 м/с к числу молекул с компонентами скорости вдоль той же оси в интервале 500±0,51 м/с.
задача 20578
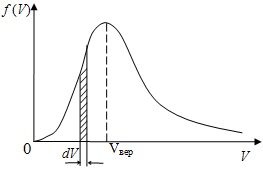
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где f(V) = dN/(N·dN) — доля молекул, скорости которых заключены в интервале от V до V+dV в расчете на единицу этого интервала. Для этой функции верным утверждением является… 1) При понижении температуры площадь под кривой уменьшается. 2) При повышении температуры максимум кривой смещается влево. 3) Площадь заштрихованной полоски с ростом температуры будет уменьшаться. 4) С уменьшением температуры величина максимума уменьшается.
задача 20581
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где f(V) = dN/(N·dN) — доля молекул, скорости которых заключены в интервале от V до V+dV в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большей молярной массой и таким же числом молекул, то ... 1) величина максимума уменьшится; 2) площадь под кривой увеличится; 3) площадь заштрихованной полоски уменьшится; 4) максимум кривой сместится влево.

задача 20586
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где f(V) = dN/(N·dN) — доля молекул, скорости которых заключены в интервале от V до V+dV в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с меньшей молярной массой и таким же числом молекул, то… 1) величина максимума увеличится; 2) площадь под кривой уменьшится; 3) максимум кривой сместится вправо, в сторону больших скоростей. 4) площадь заштрихованной полоски уменьшится.

задача 20589
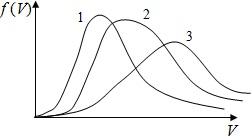
В трех сосудах находятся газы, причем для температур и масс молекул газов имеют место следующие соотношения: Т1 = Т2 = Т3, m01 = m02 = 2m03. На рисунке схематически представлены графики распределения молекул идеального газа по скоростям (распределение Максвелла) для этих газов, где f(V) = dN/(N·dV) — доля молекул, скорости которых заключены в интервале от V до V+dV в расчете на единицу этого интервала: Для графиков этих функций верными являются утверждения, что ... 1) Кривая 1 соответствует распределению по скоростям молекул газа в сосуде 2; 2) кривая 3 соответствует распределению по скоростям молекул газа в сосуде 1; 3) кривая 2 соответствует распределению по скоростям молекул газа в сосуде 2; 4) кривая 3 соответствует распределению по скоростям молекул газа в сосуде 3.
задача 20591
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где f(V) = dN/(N·dN) — доля молекул, скорости которых заключены в интервале от V до V+dV в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большей молярной массой и таким же числом молекул, то 1) величина максимума уменьшится 2) площадь под кривой увеличится 3) максимум кривой сместится влево, в сторону меньших скоростей 4) максимум кривой сместится вправо, в сторону больших скоростей.

задача 21693
За какое время остынет до температуры окружающей среды tкон = 0 °С шар радиусом R = 5 см из материала плотностью ρ = 2,6·103 кг/м3 и теплоемкостью λ = 896 Дж/(кг·К), находящийся при температуре tнач = 500 °С. Шар можно считать абсолютно черным телом; остывание происходит только за счет излучения.
задача 21694
За какое время остынет до температуры окружающей среды tкон = 0 °С шар радиусом R = 10 см из материала плотностью ρ = 7,9·103 кг/м3 и теплоемкостью λ = 500 Дж/(кг·К), находящийся при температуре tнач = 100 °С. Шар можно считать абсолютно черным телом; остывание происходит только за счет излучения.
задача 21697
За какое время остынет до температуры окружающей среды tкон = 0 °С шар радиусом R = 8 см из материала плотностью ρ = 11,3·103 кг/м3 и теплоемкостью λ = 126 Дж/(кг·К), находящийся при температуре tнач = 100 °С. Шар можно считать абсолютно черным телом; остывание происходит только за счет излучения.
задача 21701
За какое время остынет до температуры окружающей среды tкон = 0 °С шар радиусом R = 10 см из материала плотностью ρ = 2,6·103 кг/м3 и теплоемкостью λ = 896 Дж/(кг·К), находящийся при температуре tнач = 300 °С. Шар можно считать абсолютно черным телом; остывание происходит только за счет излучения.
задача 22878
Заданы начальное значения радиус–вектора r1 = 4i–3j, м и конечное r2 = –i–2j, м описывающие положения движущейся материальной точки для моментов времени t1 = 1 c и t2 = 3 c. Нарисуйте вектор перемещения рассматриваемой точки в координатах X-Y. Найдите величину средней скорости перемещения точки за этот интервал времен.
задача 23148
Движение материальной точки по двум взаимно перпендикулярным направлениям определяется уравнениями: х = 5 – 2t3 (м), y = 3 + 6t2 (м). Определить среднюю скорость перемещения в интервале от t1 = 0 с до t2 = 3 c.
задача 23351
Исходя из распределения Максвелла по абсолютным скоростям, определить среднее относительное число молекул водорода при Т = 200 К, скорости которых лежат в интервале (198÷202) м/с.
задача 23642
Получить зависимость коэффициента внутреннего трения от температуры газов. Построить график зависимости коэффициента внутреннего трения водорода от температуры в интервале от 100 до 600 К через каждые 100 К.
задача 23643
Построить график зависимости коэффициента внутренней тренировки азота от температуры в интервале 100 К ≤ Т ≤ 600 К через каждые 100 К.
задача 23818
Известно, что человеческое ухо воспринимает упругие волны в интервале частот от ν1 = 20 Гц до ν2 = 20 кГц. Каким длинам волн соответствует этот интервал в воздухе? В воде? Скорости звука в воздухе в воде равны соответственно υ1 = 340 м/с и υ2 = 1400 м/с.
задача 24459
Найдите, при какой температуре число молекул азота, скорости которых лежат в интервале 299 - 301 м/с, равно числу молекул со скоростями в интервале 599 - 601 м/с?
задача 24602
В некотором интервале температур ν молей газа, занимающих объем V0, расширяются так, что температура газа меняется по закону Т = aV–bV2, где a и b заданные константы. Определите работу газа при увеличении его объема в θ раза. Нарисуйте график процесса на р, V диаграмме. Является ли этот процесс политропным?
задача 24603
В некотором интервале температур ν молей газа, занимающих объем V0, расширяются так, что температура газа меняется по закону Т = aV–bV2, где a и b заданные константы. Определите работу газа при увеличении его объема в два раза. Нарисуйте график процесса на р, V диаграмме. Является ли этот процесс политропным?
задача 24820
При измерении сопротивления собственного полупроводника было установлено, что при температуре t1 его сопротивление равно R1 = 5657 Ом, а при температуре t2 = 57°С равно R2 = 3428 Ом. ΔE = 0,32 эВ — ширина запрещенной зоны. 1. Найдите t1. 2. Постройте график зависимости сопротивления полупроводника от температуры в интервале от t2 до t1 с шагом Δt = 3°С. 3. Найдите значения температурного коэффициента сопротивления полупроводника при температурах t2 и t1. 4. Используя справочные таблицы, определите название полупроводника.
задача 40656
Движение точки задано уравнением х = At + Bt2, где А = 4м/с, В = –0,05 м/с2 . Построить графики зависимости пути, перемещения, скорости и ускорения точки в интервале времени от t1 = 0 до t2 = 80с.
задача 40884
С высокой башни с интервалом t = 1 с бросают с нулевой начальной скоростью два камня. На каком расстоянии s друг от друга будут находиться камни в тот момент, когда скорость второго станет равной 30 м/с?
|
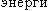 и ε которых заключены в интервале значений о
и ε которых заключены в интервале значений о 1/2εmax
1/2εmax  о εmax.
о εmax.
 о прямой согласно уравнению х = At+Bt3, где A = 6 м/с; B = 0,125 м/с3. Определить среднюю скорость <Δs/Δt> точки в интервале времени о
о прямой согласно уравнению х = At+Bt3, где A = 6 м/с; B = 0,125 м/с3. Определить среднюю скорость <Δs/Δt> точки в интервале времени о t1 = 2 c
t1 = 2 c  о t2 = 6 с.
о t2 = 6 с.

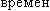 и задается уравнением s = A−Bt + Ct² + Dt³ (A = 6 м, В = 3 м/с, С = 2 м/с², D = 1 м/с³). Определите для тела в интервале времени о
и задается уравнением s = A−Bt + Ct² + Dt³ (A = 6 м, В = 3 м/с, С = 2 м/с², D = 1 м/с³). Определите для тела в интервале времени о t1 = 1 c
t1 = 1 c  о t2 = 4 c 1) среднюю скорость, 2) среднее ускорение.
о t2 = 4 c 1) среднюю скорость, 2) среднее ускорение.




