Заказать решения
Задачи по физике (рус)
Задачі з фізики (укр)
Вопросы по физике:
6 класс Другие предметы
|
точка совершает два гармонические колебания определить уравнение найти
задача 10073
Точка совершает простые гармонические колебания, уравнение которых x = Asinωt, где А = 5 с , ω = 2 с. B момент времени, , ω = 2 с. B момент времени,  да точка обладала потенциальной да точка обладала потенциальной 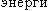 ей П = 0,1 мДж, на нее действовала возвращающая сила F = 5 мН. На ей П = 0,1 мДж, на нее действовала возвращающая сила F = 5 мН. На этот момент времени t. этот момент времени t.
задача 10074
Определить частоту ν простых гармонических колебаний диск а радиусом R = 20 с а радиусом R = 20 с около горизонтальной оси, проходя около горизонтальной оси, проходя ей через середину радиуса диска перпендикулярно ей через середину радиуса диска перпендикулярно  о плоскости. о плоскости.
задача 10075
Определить период Т простых гармонических колебаний диска радиусом R = 40 с около горизонтальной оси, проходя около горизонтальной оси, проходя ей через образующую диска. ей через образующую диска.
задача 10566
Точка совершает гармонические колебания, уравнение которых им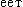 вид х = A sin ωt, где A = 5 см; ω = 2 с. B момент, вид х = A sin ωt, где A = 5 см; ω = 2 с. B момент,  да на точку действовала возвращающая сила F = +5 мН, точка обладала потенциальной да на точку действовала возвращающая сила F = +5 мН, точка обладала потенциальной 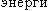 ей П = 0,1 мДж. На ей П = 0,1 мДж. На этот момент этот момент  и t и соответствующую и t и соответствующую 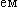 у фазу φ колебания. у фазу φ колебания.
задача 10568
Материальная точка массой m = 0,01 к совершает гармонические колебания, уравнение которых им совершает гармонические колебания, уравнение которых им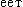 вид х = А sinωt, где A = 0,2 м; ω = 8π с–1. На вид х = А sinωt, где A = 0,2 м; ω = 8π с–1. На возвращающую силу F в момент возвращающую силу F в момент 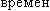 и t = 0,1 с, a также полную и t = 0,1 с, a также полную 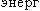 и и Е точки. Е точки.
задача 10571
Определить период Т простых гармонических колебаний диска радиусом R = 30 с около горизонтальной оси, проходя около горизонтальной оси, проходя ей через образующую диска. ей через образующую диска.
задача 10574
Точка совершает одновременно 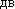 а гармонических колебания, происходящих а гармонических колебания, происходящих  о взаимно перпендикулярным направлениям и выражаемых уравнениями: x = A1cos ω1t и y = A2sin ω2t, где А1 = 1 см; ω1 = 0,5 с–1; A2 = 1 см; ω2 = 1 с–1. На о взаимно перпендикулярным направлениям и выражаемых уравнениями: x = A1cos ω1t и y = A2sin ω2t, где А1 = 1 см; ω1 = 0,5 с–1; A2 = 1 см; ω2 = 1 с–1. На уравнение траектории построить ее c соблюдением масштаба и указать направление движения. уравнение траектории построить ее c соблюдением масштаба и указать направление движения.
задача 11308
Точка совершает гармонические колебания. Наибольшее смещение xmax точки равно 10 см, наибольшая скорость 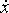 max = 20 см/с. Найти угловую частоту ω колебаний и максимальное ускорение max = 20 см/с. Найти угловую частоту ω колебаний и максимальное ускорение 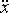 max точки. max точки.
задача 11321
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = A1cosωt и y = A2cosω(t+τ), где А1 = 4 см, A1 = 8 см, ω = π c–1, τ = 1 с. Найти уравнение траектории точки и построить график ее движения.
задача 11322
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями: 1) x = Acosωt и y = Acosωt; 2) x = Acosωt и y = A1cosωt; 3) x = Acosωt и y = Acos(ωt+φ1); 4) x = A2cosωt и y = Acos(ωt+φ2); 5) x = A1cosωt и y = A1sinωt; 6) x = Acosωt и y = A1sinωt; 7) x = A2sinωt и y = A1sinωt; 8) x = A2sinωt и y = Asin(ωt+φ2). Найти (для восьми случаев) уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 11324
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями x = A1cosωt и y = A2sinωt, где A1 = 2 см, A2 = 1 см. Найти уравнение траектории точки и построить ее, указав направление движения.
задача 12238
Уравнение гармонических колебаний дано в виде: Х = 0,2cos(2πt + π/3), м. Найти, какую долю составляет кинетическая энергия от полной энергии в момент времени t = T/6.
задача 12270
Точка совершает гармонические колебания согласно уравнению x = 0,4 sinπt (м). Определить скорость и ускорение точки через 1/6 с от начала колебаний.
задача 12277
Гармонические колебания в контуре описываются уравнением: q = 10–9cos(104t+π/2), Кл. Записать уравнение колебаний напряжения на пластинах конденсатора и тока. Емкость конденсатора равна С = 0,1 нФ.
задача 12552
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями х = cos πt и у = cos πt/2. Определить уравнение траектории точки и вычертить ее с нанесением масштаба.
задача 12874
Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х0 = 5 см, со скоростью v0 = –15 см/с. Определите амплитуду колебаний.
задача 12875
Материальная точка, совершающая гармонические колебания с частотой ν = 2 Гц, в момент времени t = 0 проходит положение, определяемое координатой х0 = 6 см, со скоростью v0 = 14 см/с. Определите амплитуду колебаний.
задача 13637
Точка совершает гармонические колебания по закону x = 3cos(πt/2+π/8), м. Определите: 1) период колебаний, 2) максимальную скорость vmax точки; 3) максимальное ускорение аmаx точки.
задача 13639
Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6sin 2πt. Запишите зависимость смещения  той точки от времени. той точки от времени.
задача 13644
Тело массой m = 10 г совершает гармонические колебания  о закону х = 0,1 cos(4t + π/4), м. Определи о закону х = 0,1 cos(4t + π/4), м. Определи те максимальные значения: 1) возвращающей силы; 2) кинетической энергии. те максимальные значения: 1) возвращающей силы; 2) кинетической энергии.
задача 13645
Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos(3πt/2), м. Определи те: 1) возвращающую силу F для момента те: 1) возвращающую силу F для момента 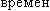 и t = 0,5 с; 2) полную и t = 0,5 с; 2) полную 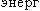 и и E точки. E точки.
задача 13646
Материальная точка массой m = 20 г совершает гармонические колебания  о закону х = 0,1 cos(4πt + π/4) м. Определи о закону х = 0,1 cos(4πt + π/4) м. Определи те полную энергию E этой точки. те полную энергию E этой точки.
задача 13648
Определите отношение кинетической 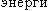 и Т точки, совершающей гармонические колебания, к ee потенциальной и Т точки, совершающей гармонические колебания, к ee потенциальной 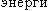 и П, и П,  ли известна фаза колебания. ли известна фаза колебания.
задача 13688
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = 3 cos 2ωt, см и у = 4 cos(2ωt + π), см. Определите уравнение траектории точки и вычертите ее с нанесением масштаба.
задача 13690
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = A sin(ωt+π/2), y = A sin ωt. Определите уравнение траектории точки и вычертите ее с нанесением масштаба, указав направление ее движения по этой траектории.
задача 13692
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = A sin ωt и у = A sin 2ωt. Определите уравнение траектории точки и вычертите ее с нанесением масштаба.
задача 13768
Один конец упругого стержня соединен c источником гармонических колебаний, подчиняющихся закону ξ = A cosωt, a другой  о конец жестко закреплен. Учитывая, о конец жестко закреплен. Учитывая,  то отражение в месте закрепления стержня происходит о то отражение в месте закрепления стержня происходит о менее плотной среды, определи менее плотной среды, определи те характер колебаний в любой точке стержня. те характер колебаний в любой точке стержня.
задача 14001
Материальная точка массой т = 0,05 кг совершает гармонические колебания, уравнение которых имеет вид: х = 0,1 sin(5t) м. Найти силу F, действующую на точку: 1) в момент, когда фаза колебания φ = 30°, 2) в положении наибольшего отклонения точки.
задача 14021
Полная энергия тела, совершающего гармонические колебания равна 30 мкДж, максимальная сила, действующая на тело, равна 1,5 мН. Написать уравнение движения этого тела, если период колебаний равен 2 с, а начальная фазa равна нулю.
задача 14125
Рука человека при ходьбе совершает гармонические колебания по уравнению x = 17sin1,6πt см. Определить время прохождения руки от положения равновесия до максимального отклонения.
задача 14358
Уравнение гармонических колебаний тела имеет вид x = 5sin π(t+0,1), см. Чему равны период и циклическая частота этих колебаний?
задача 15028
В процессе гармонических колебаний грузик математического маятника имеет максимальную скорость 3 м/с и максимальное ускорение 3,14 м/с2. Чему равен период колебаний маятника?
задача 15488
Полная энергия тела, совершающего гармоническое колебательное движение, W = 30 мкДж; максимальная сила, действующая на тело, Fmax = 1,5 мН. Написать уравнение движения этого тела, если период колебаний T = 2 с и начальная фаза φ = π/3.
задача 15575
Период гармонических колебаний математического маятника уменьшается в 2 раза. На сколько процентов возрастет при этом частота колебаний?
задача 15696
Постройте в тетради графики и спектры гармонических колебаний, заданных следующими временными зависимостями: x1 = 2 sin πt, х2 = sin 2πt. Выполните сложение этих колебаний, расположите графики точно один под другим. Постройте спектры колебаний.
задача 15927
Определить полную энергию точки массой 20 г, совершающей гармонические колебания x = 0,15cos(4πt+π/5) (м), а также определить силу, действующую на точку в момент времени t = 0,2 с.
задача 15967
Математический маятник массой m = 100 г и длиной l = 1 м совершает гармонические колебания по закону x = 2,5sin2πt см. Определить натяжение в момент времени t = T/4.
задача 16105
По заданному уравнению x = 20 cos 2πt (см) гармонических колебаний пружинного маятника определить основные параметры колебательной системы (xm, ω, ν, T, k), нарисовать графики зависимости координаты, скорости и ускорения от времени. m = 10 г.
задача 17925
Частица участвует в двух гармонических колебаниях, проходящих вдоль одного направления. Частота одинакова для обоих колебаний и равна 9 Гц, начальные фазы имеют значения π/6 рад и 0 рад, амплитуды соответственно равны 7 см и 4 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебаний, запишите его уравнение.
задача 18129
Материальная точка совершает гармонические колебания. Наибольшее смещение точки 25 см, наибольшая скорость 50 см/с. Найти максимальное ускорение точки и ее смещение через 2 с.
задача 18130
Материальная точка массой 0,2 кг совершает гармонические колебания, уравнение которых имеет вид х = A sin ωt, где А = 0,4 м; ω = 30 рад/с. Найти полную энергию точки и возвращающую силу в момент времени 0,2 с.
задача 18134
Максимальная сила, действующая на тело, совершающее гармоническое колебание, равна 2·10–3 Н, полная энергия равна 5·10–5 Дж. Написать уравнение движения этого тела, если период колебаний 3 с и начальная фаза 30°.
задача 18953
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями х = 3cosωt, см и у = 4cosωt, см. Определите уравнение траектории точки и вычертите её с нанесением масштаба.
задача 19608
Математический маятник массой m = 10 г и длиной l = 10 м совершает гармонические колебания по закону α = 0,25·sin2πt. Определить силу натяжения в момент времени t = T/2.
задача 19945
Материальная точка совершает гармонические колебания по закону x = xmsinω0t. График, на котором изображена зависимость проекции ускорения ax этой точки от времени t, приведен под номером ...

задача 19950
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = 4cosπt см и y = 8cos(πt+π) см. Найдите уравнение траектории точки и постройте график ее движения.
задача 19955
Материальная точка совершает колебания по закону x = xmcosω0t. Зависимость проекции vx скорости этой точки от времени t приведена на графике под номером ...

задача 20109
Точка совершает гармонические колебания c частотой 10 Гц. B момент, принятый  а начальный, точка имела максимальное смещение 1 мм. Написать уравнение колебаний точки и начертить и а начальный, точка имела максимальное смещение 1 мм. Написать уравнение колебаний точки и начертить и график. график.
задача 21121
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Уравнения колебаний х = A cos ωt и у = A cos (ωt + φ). Определить уравнение траектории точки в виде f(x, у) = 0. Принять А = 2 см, φ = π/2.
задача 21409
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями х = 4 cos πt см и у = 2 sin π(t + 1) см. Найти уравнение траектории точки и построить график ее движения.
задача 21744
Уравнение колебаний звучащего камертона имеет вид: Δр(t) = 0,003sin(800πt), Па. Звук, издаваемый камертоном, распространяется в воздухе в виде плоской волны при нормальном атмосферном давлении и температуре 17° С. Вычислите скорость распространения волны и звуковое давление в точке М, находящейся на расстоянии 10 м от камертона через 0,03 с после начала колебаний. Газ считать двухатомным с молярной массой 29 кг/кмоль.
задача 21756
Написать уравнение движения x(t) частицы, одновременно участвующей в двух колебаниях одного направления: x1 = 30cos πt/3 и x2 = 30cos(πt/3 + π/6) (мм).
задача 21985
Точка массой 5 г совершает гармоническое колебание закону x = 5sin(3/5πt + π/3) (см). Написать уравнения колебаний кинетической и потенциальной энергии точки: определить полную энергию точки.
задача 22014
Материальная точка участвует одновременно в двух гармонических колебаниях, проходящих вдоль одной прямой. В единицах СИ уравнения слагаемых колебаний записываются в виде x1 = 0,1cos π(t+1/6) и x2 = 0,05cos π(t+1/2). Определить уравнение результирующих колебаний.
задача 22015
Материальная точка участвует одновременно в двух гармонических колебаниях, проходящих вдоль одной прямой. В единицах СИ уравнения слагаемых колебаний записываются в виде x1 = 0,1cos πt/2 и x2 = 0,12 cos π(t+1)/2. Определить уравнение результирующих колебаний.
задача 22141
Уравнение гармонических колебаний имеет вид х = Acos(ωt). Известно, что при фазе π/6 рад смешение равно 2 см. Определить смешение и скорость точки при фазе 3π/4 рад, если период колебаний Т = 2 с.
задача 22191
Полная энергия тела, совершающего гармонические колебания, равна 45 мкДж, максимальная сила, действующая на тело, равна 2 мН. Написать уравнение движения этого тела, если период колебаний равен 3 с и начальная фаза 30° (косинусоидальная зависимость).
задача 22225
Уравнение колебаний у ножки звучащего камертона имеет вид: Δр(t) = 0,003sin(800πt), Па. Звук, издаваемый камертоном, распространяется в воздухе (μ = 29 кг/кмоль) при нормальном атмосферном давлении и температуре 17° С. Определить: 1) скорость распространения волны; 2) звуковое давление в точке М, находящейся на расстоянии y(M) = 10 м от камертона через t = 0,03 с после начала колебаний. Газ считать двухатомным (γ = 7/5), волну плоской.
задача 22635
Материальная точка участвует одновременно в двух гармонических колебаниях, проходящих вдоль одной прямой. В единицах СИ уравнения слагаемых колебаний записываются в виде x1 = 0,1cos πt/2 и x2 = 0,12cos π(t+1)/2. Определить уравнение результирующих колебаний.
задача 22843
Материальная точка совершает гармонические колебания. Наибольшее смещение точки равно xmax = 10 см, а наибольшая скорость υmax = 20 см/с. Определить циклическую частоту колебаний ω и максимальное ускорение amax точки.
задача 23448
Материальная точка массой m = 20 г совершает гармонические колебания по закону х = 0,2 cos(2πt + π/6) м. Определить максимальное значение скорости частицы vmax и полную энергию W этой точки.
задача 23455
Материальная точка массы m = 10 г под действием упругой силы совершает гармонические колебания по закону х = Аcos(ω0t + φ0), где А = 5,0 см, ω0 = 3 рад/с, φ0 = π рад. Определить модуль упругой силы, действующей на материальную точку в момент времени t = 3 с после начала колебаний.
задача 23457
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями х = А1cos ωt и у = А2cos ω(t + τ), где А1 = 4 см, А2 = 8 см, ω = π с–1, τ = 1 с. Найти уравнение траектории точки и построить ее с соблюдением масштаба, указав направление движения точки. Поясните свой ответ.
задача 23471
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: x = 2cosωt см и y = cosωt см. Запишите уравнение траектории результирующего движения точки и постройте ее с соблюдением масштаба.
задача 23609
Определить натяжение нити в момент t, если математический маятник массой m, длиной l совершает гармонические колебания по заданному закону а = а0 sin(ωt + φ).
задача 24057
Полная энергия тела, совершающего гармоническое колебательное движение, равна 30 мкДж; максимальная сила, действующая на тело, равна 1,5 мН. Написать уравнение движения этого тела, если период колебаний равен 2 с и начальная фаза равна π/3.
задача 24098
Точка совершает колебания, описываемые уравнением: x = 5 sin(0,1πt), см. В некоторый момент времени сила, действующая на точку, и её потенциальная энергия соответственно равны 2·10–2 Н и 5·10–4 Дж. Чему равны фаза колебаний и кинетическая энергия точки в этот момент времени?
задача 24506
Материальная точка совершает гармонические колебания, уравнение которых имеет вид х = 0,05 sin (2t + π/4) м. Определить период колебаний, а также момент времени (ближайший к началу отсчета), в который потенциальная энергия точки равна Wp = 1·10–4 Дж, а возвращающая сила F = 5·10–3 Н.
задача 24735
Точка совершает гармонические колебания. Наибольшее смещение точки равно 10 см, наибольшая скорость 20 см/с. Найти угловую частоту колебаний и максимальное ускорение точки.
задача 24736
Приведены уравнения гармонических колебаний четырех систем с различными коэффициентами упругости k и одинаковыми массами m. В каком случае коэффициент упругости наименьший? Подтвердите Ваш выбор расчетами. 1) х = 2 cos(3πt + π), см 2) х = 3 cos(2πt + π), см 4) х = 3 cos(5πt + π/2), см 8) х = 4 cos(4πt + π/2), см.
задача 24738
Материальная точка совершает гармонические колебания по закону косинуса. Найти отношение кинетической энергии Wk точки, к ее потенциальной энергии Wp для моментов времени t = T/12, t = T/8 и t = T/6.
задача 25181
Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярных направлениях по уравнениям: х = A cos 2ωt и у = A1 cos ωt. Определить уравнение траектории точки. Принять: А = 2 см; А1 = 3 см.
задача 26197
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = Acosωt и y = Acosωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 26198
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = Acosωt и y = A1cosωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 26199
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = Acosωt и y = Acos(ωt+φ1). Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 26200
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = A2cosωt и y = Acos(ωt+φ2). Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 26201
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = A1cosωt и y = A1sinωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 26202
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = Acosωt и y = A1sinωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 26203
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = A2sinωt и y = A1sinωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 26204
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = A2sinωt и y = Asin(ωt+φ2). Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A1 = 3 см, А2 = 1 см; φ1 = π/2, φ2 = π.
задача 26322
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: x = sin ωt/2; y = cosωt. Найти уравнение траектории точки и построить график ее движения.
задача 26535
Тело массой 10 г совершает гармонические колебания по закону x = 0,1cos(4πt+π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.
задача 26671
Определить возвращающую силу F в момент времени t = 0,2 c и полную энергию Е точки массой m = 20 г, совершающей гармонические колебания согласно уравнению х = A·sin(ωt), где А = 0,15 м и ω = 4π с–1.
задача 40142
Математический маятник массой m = 100 г и длиной l = 1 м совершает гармонические колебания  о закону α = 0,25sin2πt. Определить натяжение в момент времен о закону α = 0,25sin2πt. Определить натяжение в момент времен и t = T/2. и t = T/2.
задача 40604
Чему равно отношение кинетической 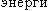 и точки, совершающей гармонические колебания, к ee потенциальной и точки, совершающей гармонические колебания, к ee потенциальной 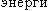 и для момента и для момента 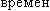 и t = T/12, где Т – период колебаний. и t = T/12, где Т – период колебаний.
задача 40631
Материальная точка массой m = 0,01 кг совершает гармонические колебания, уравнение которых имеет вид x = 0,2 sin 8πt (длина выражена в сантиметрах, время — в секундах). Найти возвращающую силу F в момент времени t = 0,1 с, а также полную энергию Е точки.
задача 40717
Полная 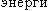 я тела массой 1 к я тела массой 1 к , совершающего гармонические колебания равна, 10 Дж, максимальная возвращающая сила, действующая на тело составляет 100 Н. Написать уравнение колебательного движения тела, , совершающего гармонические колебания равна, 10 Дж, максимальная возвращающая сила, действующая на тело составляет 100 Н. Написать уравнение колебательного движения тела, 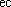 ли начальная фаза равна 45°. ли начальная фаза равна 45°.
задача 40781
Полная энергия тела, совершающего гармонические колебания, равна Е = 3·10–5 Дж. Максимальная сила, действующая на тело, равна F = 1,5·10–3 Н. Написать уравнение движения этого тела, если период колебаний равен Т = 2 с и начальная фаза 60°.
|
 , ω = 2 с. B момент времени,
, ω = 2 с. B момент времени,  да точка обладала потенциальной
да точка обладала потенциальной 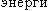 ей П = 0,1 мДж, на нее действовала возвращающая сила F = 5 мН. На
ей П = 0,1 мДж, на нее действовала возвращающая сила F = 5 мН. На этот момент времени t.
этот момент времени t.
 около горизонтальной оси, проходя
около горизонтальной оси, проходя ей через середину радиуса диска перпендикулярно
ей через середину радиуса диска перпендикулярно  о плоскости.
о плоскости.
 около горизонтальной оси, проходя
около горизонтальной оси, проходя ей через образующую диска.
ей через образующую диска.
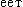 вид х = A sin ωt, где A = 5 см; ω = 2 с. B момент,
вид х = A sin ωt, где A = 5 см; ω = 2 с. B момент,  да на точку действовала возвращающая сила F = +5 мН, точка обладала потенциальной
да на точку действовала возвращающая сила F = +5 мН, точка обладала потенциальной 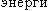 ей П = 0,1 мДж. На
ей П = 0,1 мДж. На этот момент
этот момент 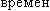 и t и соответствующую
и t и соответствующую 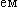 у фазу φ колебания.
у фазу φ колебания.
 совершает гармонические колебания, уравнение которых им
совершает гармонические колебания, уравнение которых им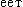 вид х = А sinωt, где A = 0,2 м; ω = 8π с–1. На
вид х = А sinωt, где A = 0,2 м; ω = 8π с–1. На возвращающую силу F в момент
возвращающую силу F в момент 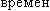 и t = 0,1 с, a также полную
и t = 0,1 с, a также полную 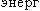 и
и Е точки.
Е точки.
 около горизонтальной оси, проходя
около горизонтальной оси, проходя ей через образующую диска.
ей через образующую диска.
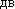 а гармонических колебания, происходящих
а гармонических колебания, происходящих  о взаимно перпендикулярным направлениям и выражаемых уравнениями: x = A1cos ω1t и y = A2sin ω2t, где А1 = 1 см; ω1 = 0,5 с–1; A2 = 1 см; ω2 = 1 с–1. На
о взаимно перпендикулярным направлениям и выражаемых уравнениями: x = A1cos ω1t и y = A2sin ω2t, где А1 = 1 см; ω1 = 0,5 с–1; A2 = 1 см; ω2 = 1 с–1. На уравнение траектории построить ее c соблюдением масштаба и указать направление движения.
уравнение траектории построить ее c соблюдением масштаба и указать направление движения.
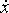 max = 20 см/с. Найти угловую частоту ω колебаний и максимальное ускорение
max = 20 см/с. Найти угловую частоту ω колебаний и максимальное ускорение 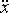 max точки.
max точки.
 той точки от времени.
той точки от времени.
 о закону х = 0,1 cos(4t + π/4), м. Определи
о закону х = 0,1 cos(4t + π/4), м. Определи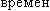 и t = 0,5 с; 2) полную
и t = 0,5 с; 2) полную 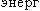 и
и E точки.
E точки.
 о закону х = 0,1 cos(4πt + π/4) м. Определи
о закону х = 0,1 cos(4πt + π/4) м. Определи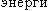 и Т точки, совершающей гармонические колебания, к ee потенциальной
и Т точки, совершающей гармонические колебания, к ee потенциальной 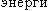 и П,
и П, 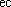 ли известна фаза колебания.
ли известна фаза колебания.
 о конец жестко закреплен. Учитывая,
о конец жестко закреплен. Учитывая,  то отражение в месте закрепления стержня происходит о
то отражение в месте закрепления стержня происходит о менее плотной среды, определи
менее плотной среды, определи

 а начальный, точка имела максимальное смещение 1 мм. Написать уравнение колебаний точки и начертить и
а начальный, точка имела максимальное смещение 1 мм. Написать уравнение колебаний точки и начертить и график.
график.
 о закону α = 0,25sin2πt. Определить натяжение в момент времен
о закону α = 0,25sin2πt. Определить натяжение в момент времен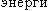 и точки, совершающей гармонические колебания, к ee потенциальной
и точки, совершающей гармонические колебания, к ee потенциальной 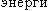 и для момента
и для момента 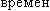 и t = T/12, где Т – период колебаний.
и t = T/12, где Т – период колебаний.
 я тела массой 1 к
я тела массой 1 к , совершающего гармонические колебания равна, 10 Дж, максимальная возвращающая сила, действующая на тело составляет 100 Н. Написать уравнение колебательного движения тела,
, совершающего гармонические колебания равна, 10 Дж, максимальная возвращающая сила, действующая на тело составляет 100 Н. Написать уравнение колебательного движения тела,  ли начальная фаза равна 45°.
ли начальная фаза равна 45°.