Заказать решения
Задачи по физике (рус)
Задачі з фізики (укр)
Вопросы по физике:
6 класс Другие предметы
Витамины для ума Лучшая книга о разуме
|
вращается вокруг оси с угловой скоростью радиус определить массу
задача 10053
Платформа в виде диска диаметром D = 3 м и массой m1 = 180 к  же же вращаться вокруг вертикальной оси. С как вращаться вокруг вертикальной оси. С как угловой скоростью будет вращаться угловой скоростью будет вращаться  та платформа, если та платформа, если  о ee краю пойдет человек массой m2 = 70 к о ee краю пойдет человек массой m2 = 70 к со скоростью v = 1,8 м/с относительно платформы? со скоростью v = 1,8 м/с относительно платформы?
задача 10057
Ha краю платформы в виде диска, вращающейся  о инерции вокруг вертикальной оси c частотой n1 = 8 мин–1, стоит человек массой m1 = 70 к о инерции вокруг вертикальной оси c частотой n1 = 8 мин–1, стоит человек массой m1 = 70 к . .  да человек перешел в центр платформы, да человек перешел в центр платформы,  на стала вращаться c частотой n2 = 10 мин–1. О на стала вращаться c частотой n2 = 10 мин–1. О ить массу m2 платформы. Момент инерции человека рассчитывать ить массу m2 платформы. Момент инерции человека рассчитывать  к для материальной точки. к для материальной точки.
задача 10059
Горизонтальная платформа массой m1 = 150 к вращается вокруг вертикальной оси, проходящей чepeз центр платформы, c частотой n = 8 мин–1. Человек массой m2 = 70 к вращается вокруг вертикальной оси, проходящей чepeз центр платформы, c частотой n = 8 мин–1. Человек массой m2 = 70 к стоит при стоит при  том на краю платформы. C какой угловой скоростью ω начнет вращаться платформа, том на краю платформы. C какой угловой скоростью ω начнет вращаться платформа,  ли человек перейдет о ли человек перейдет о края платформы к ee центру? Считать платформу круглым, однородным диском, a человека — материальной точкой. края платформы к ee центру? Считать платформу круглым, однородным диском, a человека — материальной точкой.
задача 10553
Платформа в виде диска радиусом R = l м вращается  о инерции c частотой n1 = 6 об/мин. Ha краю платформы стоит человек, масса которого m = 80 к о инерции c частотой n1 = 6 об/мин. Ha краю платформы стоит человек, масса которого m = 80 к . C как . C как частотой будет вращаться платформа, частотой будет вращаться платформа,  ли человек перейдет в ee центр? Момент инерции платформы J = 120 кг·м2. Момент инерции человека рассчитывать, ли человек перейдет в ee центр? Момент инерции платформы J = 120 кг·м2. Момент инерции человека рассчитывать,  к для материальной точки. к для материальной точки.
задача 11029
Линейная скорость v1 точек на окружности вращающегося диска равна 3 м/с. Точки, расположенные на ΔR = 10 см ближе к оси, имеют линейную скорость v2 = 2 м/с. Определите частоту вращения n диска.
задача 11037
Диск вращается с угловым ускорением ε = –2 рад/с2. Сколько оборотов N сделает диск при изменении частоты вращения от n1 = 240 мин–1 до n2 = 90 мин–1? Найти время Δt, в течение которого это произойдет.
задача 11087
По плоскости диска радиуса R = 10 см равномерно распределен заряд с поверхностной плоскостью σ = 0,5 нКл/см2. Диск равномерно вращается с частотой n = 1,8·103 об/мин вокруг оси, проходящей через центр диска перпендикулярно его плоскости. Определить магнитный момент рт, создаваемый вращающимся диском.
задача 11159
Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид φ = A+Bt2+Ct3, где В = 4 рад/с2, С = –1 рад/с3. Найти закон изменения момента сил, действующих на шар. Определить момент сил М в момент времени t = 2 с.
задача 11178
Пуля массой m = 10 г летит со скоростью v = 800 м/с, вращаясь около продольной оси с частотой n = 3000 с–1. Принимая пулю за цилиндрик диаметром d = 8 мм, определить полную кинетическую энергию Т пули.
задача 11371
Стержень массой 3 кг и длиной 1,5 м вращается вокруг оси, проходящей через один из его концов, по закону φ = 6+4t+2t2. Определить момент силы, действующей на другой его конец.
задача 11410
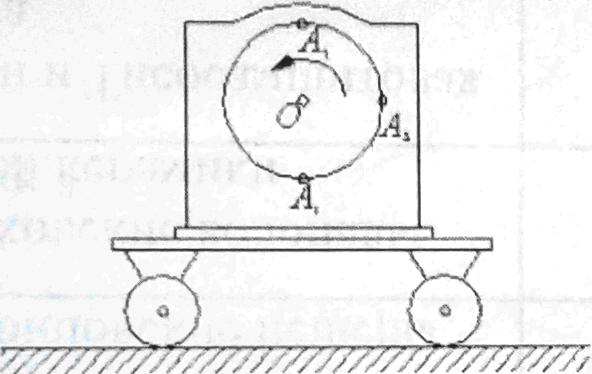
Тележка движется со скоростью v. На ней вращается диск с угловой скоростью ω. Радиус ротора равен r. Определить абсолютные скорости трех точек ротора, указанных на рисунке.
задача 11875
Диск вращается вокруг оси, проводящий через его центр масс. Зависимость угла поворота от времени имеет вид φ(t) = –4 + 2π(t + t2) (рад). Для момента времени t1 = 2 с найти: 1) сколько оборотов сделает диск; 2) угловую скорость; 3) угловое ускорение. Определить для точки, находящейся на расстоянии r = 0,1 м от оси вращения, полное линейное ускорение в момент времени t2, когда диск совершил N = 2 оборота.
задача 12620
Горизонтальная платформа, имеющая форму диска, вращается вокруг вертикальной оси, делая 10 об/мин. На краю платформы стоит человек, масса которого 60 кг. Определить частоту вращения, если человек перейдет в центр платформы. Масса платформы 250 кг, ее радиус 3,5 м. Человека считать точечной массой.
задача 12715
Платформа, имеющая форму диска, вращается около вертикальной оси с частотой n1 = 10 мин–1. На краю платформы стоит человек. С какой частотой n2 будет вращаться платформа, если человек перейдет к ее центру? Масса платформы m1 = 280 кг, масса человека m2 = 80 кг. Платформу считать круглым однородным диском, а человека – точечной массой.
задача 13027
Колесо вращается с постоянным угловым ускорением ε = 3 рад/с. Определите радиус колеса, если через t = 1 с после начала движения полное ускорение колеса а = 7,5 м/с2.
задача 13133
Шар радиусом R = 10 с и массой m = 5 к и массой m = 5 к вращается вокруг оси симметрии согласно уравнению φ = А + Вt² + Сt³ (В = 2 рад/с², С = −0,5 рад/с³). О вращается вокруг оси симметрии согласно уравнению φ = А + Вt² + Сt³ (В = 2 рад/с², С = −0,5 рад/с³). О и и те момент сил М для t = 3 с. те момент сил М для t = 3 с.
задача 13153
Человек массой m = 60 к , стоящий на краю горизонтальной платформы массой М = 120 к , стоящий на краю горизонтальной платформы массой М = 120 к , вращающейся , вращающейся  о инерции вокруг неподвижной вертикальной оси c частотой n1 = 10 мин−1, переходит к ee центру. Считая платформу круглым однородным диском, a человека - точечной массой, определите, c как о инерции вокруг неподвижной вертикальной оси c частотой n1 = 10 мин−1, переходит к ee центру. Считая платформу круглым однородным диском, a человека - точечной массой, определите, c как частотой n2 будет тогда вращаться платформа. частотой n2 будет тогда вращаться платформа.
задача 13171
Две материальные точки массами m1 и m2 расположены друг о друга на расстоянии R. Определите угловую скорость вращения, c которой друга на расстоянии R. Определите угловую скорость вращения, c которой  ни должны вращаться вокруг общего центра масс, ни должны вращаться вокруг общего центра масс,  бы расстояние между ними осталось постоянным. бы расстояние между ними осталось постоянным.
задача 13447
Диск массы m и радиуса R равномерно вращается вокруг своей оси с угловой скоростью ω. Под действием внешних сил диск останавливается. Чему равна работа А внешних сил?
задача 13828
Диск массой 2 кг и радиусом 0,1 м вращается вокруг оси, проходящей через его центр. Уравнение движения φ = 5 – 6t 2 + t3. Определить момент сил, действующих на диск, в момент времени 4 с. Определишь закон изменения момента сил.
задача 13829
Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через ее центр. Уравнение вращения шара имеет вид: φ = 2+4t2–t3. Найти закон изменения момента сил, действующих на шар. Определить момент сил в момент времени 2 с.
задача 13840
Горизонтальная платформа массой 250 кг вращается вокруг вертикальной оси, делая 10 об/мин. На краю платформы стоит человек — точечная масса 80 кг. Во сколько раз увеличится кинетическая энергия платформы, если человек переместится на 0,5R к центру платформы? (R — радиус платформы).
задача 14238
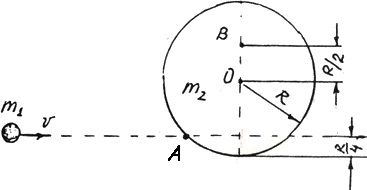
Однородный диск может свободно вращаться вокруг горизонтальной оси, проходящей через его центр О. В точку А на образующей диска попадает горизонтально летящий маленький пластилиновый шарик и прилипает к его поверхности. Скорость v шарика равна 10 м/с. Определить линейную скорость u точки В на диске в начальный момент времени. Масса m1 шарика равна 10 г. Масса m2 диска равна 0,1 кг.
задача 14451
Вал вращается с частотой n = 180 об/мин. С некоторого момента вал начинает вращаться равнозамедленно с угловым ускорением ε = 3 рад/с2. Через какое время t вал остановится? Найти число оборотов N вала до остановки.
задача 14460
Колесо вращается с угловым ускорением ε = 2 рад/с2. Через время t = 0,5 с после начала движения полное ускорение колеса а = 13,6 см/с2. Найти радиус R колеса.
задача 14539
Металлический диск радиуса R вращается с угловой скоростью ω вокруг оси, перпендикулярной диску и проходящей через его центр. Найти величину вектора напряженности электрического поля, возникшего на краю диска.
задача 14640
Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого J = 50кг·м2 и радиус R = 20 см. Момент сил трения вращающегося блока Mтр = 98,1 Н·м. Найти разность сил натяжения нити T1–Т2 по обе стороны блока, если известно, что блок вращается с угловым ускорением ε = 2,36 рад/с2. Блок считать однородным диском.
задача 14666
Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой n2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека — точечной массой.
задача 14670
Человек массы m0 = 60 кг стоит на неподвижной платформе массы m = 100 кг. С какой частотой n завращаться платформа, если человек пойдет по окружности радиусом r = 5 м вокруг оси вращения? Скорость движения человека относительно платформы v0 = 4 км/ч. Радиус платформы R = 10 м. Считайте платформу однородным диском, человека — материальной точкой.
Задача 23952
Молекулу NO2 можно смоделировать треугольником, в вершинах которого находятся ядра атомов. Угол между ядрами кислорода равен 140°. Расстояние между ядрами азота и кислорода равно 0,118 нм. Определите радиус окружности, описываемой ядром азота, считая, что молекула вращается вокруг оси, перпендикулярной ее плоскости и проходящей через центр масс.
Задача 24042
Два горизонтальных диска свободно вращаются в разных направлениях вокруг вертикальной оси, проходящей через их центры. Массы дисков равны 10 кг и 40 кг, их радиусы 0,2 м и 0,1 м, угловые скорости 10 рад/с и 20 рад/с соответственно. После падения верхнего диска на нижний оба диска благодаря трению между ними начали через некоторое время вращаться как единое целое. Найдите изменение суммарной кинетической энергии дисков.
задача 14690
Тело вращается так, что зависимость угловой скорости от времени определяется уравнением; ω = 2+0,5t. Найти полное число оборотов, совершенных телом за 20 с после начала вращения. Указать начальную угловую скорость и ускорение тела.
задача 15000
На краю карусели, имеющей форму диска, массой 200 кг и диаметром 4 м, вращающейся с частотой 1 об/с, стоят пять человек, каждый массой по 60 кг. Найти частоту вращения карусели, если все люди сместятся к ее центру на половину радиуса. Считать, что по сравнению с размером карусели люди представляют собой материальные точки.
задача 15026
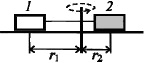
Тележки связанны нитью и вращаются не смещаясь на центробежной машине. Определите массу второй тележки, если r1 = 30 см; r2 = 10 см, а масса первой тележки равна 300 г.
задача 15037
Человек массой 80 кг находится на неподвижной круглой платформе радиусом 20 м и массой 200 кг, которая может вращаться вокруг своей вертикальной оси. С какой угловой скоростью будет вращаться платформа, если человек будет двигаться по окружности радиусом 10 м с линейной скоростью 2,5 м/с относительно платформы?
задача 15453
Человек массой m находится на неподвижной круглой платформе массой M и радиусом R, которая может вращаться вокруг вертикальной оси симметрии платформы. С какой угловой скоростью будет вращаться платформа, если человек начнет двигаться по окружности радиусом r со скоростью v относительно платформы?
задача 15613
Какую минимальную скорость V должен иметь математический маятник, проходя через положение устойчивого равновесия, для того чтобы он мог вращаться по кругу в вертикальной плоскости?
задача 15888
Определите период обращения вокруг Земли спутника, который удален от поверхности Земли на расстояние, равное трем радиусам Земли.
задача 16064
Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Зависимость угла поворота шара от времени имеет вид: φ = Сt2, где С = 10 рад/с2. Определить момент сил, действующих на шар.
задача 16598
Обруч радиусом R, который вращается около вертикальной оси, перпендикулярной к плоскости обруча и проходящей через его центр, с угловой скоростью ω0, опускают на горизонтальную поверхность. Коэффициент трения обруча о поверхность
задача 16714
Колесо вращается вокруг неподвижной оси с угловым ускорением ε = At2 + В, где А = 12 рад/с4, В = 4 рад/с2. На какой угол повернется колесо через 2 с, если в начальный момент времени угловая скорость ω0 = 0 и угол поворота φ0 = 0.
задача 18193
Лента перематывается с одной катушки на другую. Скорость подачи ленты постоянна и равна ν. Найти угловую скорость вращения мотка через время t после начала перемотки. Начальный радиус мотка r0, толщина ленты Δl.
задача 18269
Платформа, представляющая собой однородный сплошной цилиндр массой 200 кг и радиусом 2 м, на краю которой стоит человек массой 80 кг, вращается без трения вокруг вертикальной оси с частотой 18 об/мин. Человек начал двигаться по краю платформы со скоростью 2 м/с относительно нее в направлении ее вращения? С какой частотой стала вращаться платформа. Человека рассматривать как материальную точку.
задача 19581
Спутник вращается вокруг Земли в плоскости экватора. Определите высоту орбиты h, если за сутки спутник совершает n = 14 оборотов вокруг Земли.
задача 19670
Однородный тонкий стержень, находящийся на гладкой горизонтальной поверхности, свободно вращается вокруг своего конца с некоторой угловой скоростью ω0. В некоторый момент ось вытаскивают, и стержень скользит по плоскости, вращаясь. Определить угловую скорость этого вращения.
задача 19689
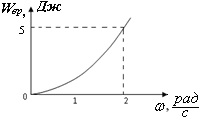
На рисунке дан график зависимости энергии вращающегося тела Wвр от угловой скорости. Чему будет равен момент импульса тела, при величине угловой скорости равной ω = 4 рад/с?
задача 19853
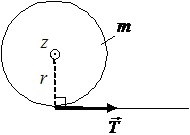
На однородный сплошной цилиндр радиуса r = 0,2 м и массы m = 1 кг, который может вращаться вокруг оси, совпадающей с его осью симметрии (ось z), намотана нить. За нить тянут так, что зависимость угла поворота цилиндра от времени имеет вид φ(t) = Bt3, где B = 10 рад·с–3. Определить силу натяжения нити через две секунды после начала вращения цилиндра, если со стороны оси на вращающийся цилиндр действует постоянный тормозящий момент, величина которого |Mтр| = 1 Н·м.
задача 19854
Однородный шар радиуса r = 0,1 м и массы m = 2 кг может вращаться вокруг оси z, проходящей через его центр. На "экватор" шара намотана нить, за которую тянут так, что зависимость угла поворота шара от времени имеет вид φ(t) = Bt4, где B = 1 рад·с–4. Определить силу натяжения нити через две секунды после начала вращения шара, если со стороны оси на вращающийся шар действует постоянный тормозящий момент, величина которого |Mтр| = 10 Н·м.

задача 19863
Однородный сплошной цилиндр радиусом r = 0,5 м и массой m = 2 кг может вращаться вокруг горизонтальной оси (точка О). Его отклонили из положения равновесия на угол 90° и отпустили. Определить постоянный момент силы трения, который ось прикладывает к цилиндру, если при прохождении положения равновесия угловая скорость цилиндра ω = 5 рад/с.
задача 19908
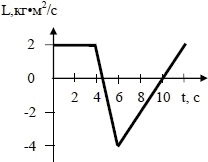
На рисунке дан график зависимости момента импульса шара, вращающегося вокруг оси, проходящей через его центр, от времени. 1) Построить график зависимости момента силы, действующей на шар, от времени. 2) Определить величину угловой скорости и углового ускорения шара при t = 2 с. Масса шара 1 кг, радиус шара 50 см.
задача 19917
Диск радиусом 10 см и массой 2 кг вращается вокруг оси, проходящей перпендикулярно его плоскости через середину радиуса. Закон движения диска φ = 6 + 4t – t2 (рад). Определить момент силы, действующей на диск, и кинетическую энергию диска через 2 с после начала вращения диска. Построить график зависимости момента силы и момента импульса диска от времени.
задача 20144
Человек массой 70 кг, стоящий на краю платформы радиусом 2 м и массой 100 кг, бросает по касательной к краю груз массой 2 кг со скоростью 4 м/с. С какой угловой скоростью начнет вращаться платформа?
задача 20370
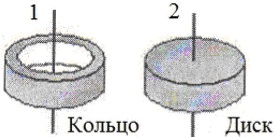
На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Кинетическая энергия первого тела Wк1вр = 0,5 Дж. Найдите момент импульса второго тела, если m = 1 кг, R = 10 см.
задача 20406
Тонкий диск с постоянной плотностью заряда вращается вокруг оси, проходящей через центр перпендикулярно плоскости диска. Радиус диска а, заряд Q, угловая скорость вращения ω. Найдите индукцию магнитного поля в центре диска.
задача 20455
Сплошной диск массой 0,2 кг вращается вокруг оси, проходящей через его центр масс под действием момента сил 0,8·10–2 Н·м. Закон вращения имеет вид φ = 5–t+2t2. Определить радиус диска.
задача 20744
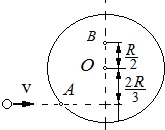
Однородный диск радиусом R = 20 см и массой m1 = 0,20 кг может свободно вращаться вокруг неподвижной горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем. В точку А на образующей диска попадает пластилиновый шарик, летящий горизонтально со скоростью v = 10 м/с, и прилипает к его поверхности. Масса шарика m2 = 10 г. Определите угловую скорость диска и линейную скорость точки В сразу после прилипания шарика(см. рис.).
задача 20869
По сфере радиуса R = 10 см равномерно распределен заряд Q = 10–8 Кл. Сфера вращается с частотой f = 10 1/c относительно оси, проходящей через центр сферы. Найти магнитный момент кругового тока, создаваемого вращающейся сферой.
задача 21102
Горизонтальная платформа в форме диска (m1 = 100 кг; R = 1,5 м) вращается вокруг своей оси, совершая 10 оборотов в минуту. Человек (m2 = 60 кг) стоит на краю платформы. Какой будет частота вращения, если человек перейдёт от края платформы к центру?
задача 21385
Тонкий стержень массой m и длиной l вращается с угловой скоростью 10 с–1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Продолжая вращаться в той же плоскости, стержень перемещается так, что ось вращения теперь проходит через конец стержня. Найти угловую скорость во втором случае.
задача 21418
Платформа в виде сплошного диска радиусом 1,5 м и массой 180 кг вращается по инерции около вертикальной оси с частотой ν = 10 мин–1. На краю платформы стоит человек массой 60 кг. Какую угловую скорость будет иметь платформа, если человек перейдет в центр платформы?
задача 21528
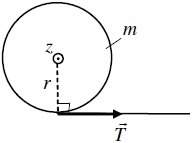
Однородный сплошной цилиндр, имеющий радиус r = 0,1 м и массу m = 1 кг, может вращаться вокруг оси, совпадающей с его осью симметрии (ось z). На цилиндр намотана нить, за которую тянут так, что зависимость угла поворота цилиндра от времени имеет вид φ(t) = Bt5, где B = 1 рад·с–5. Определить момент времени, когда сила натяжения нити T станет равной 28 Н, если со стороны оси на вращающийся цилиндр действует постоянный тормозящий момент, величина которого |Mтр| = 2 Н·м.
задача 21572
Человек массой 70 кг, стоящий на краю горизонтальной платформы массой 1000 кг, вращающейся вокруг неподвижной вертикальной оси с угловой скоростью 0,2 рад/с, переходит к ее центру. Считая платформу однородным диском, а человека – материальной точкой, определите, с какой частотой будет вращаться платформа после этого перехода.
задача 22406
Платформа в виде горизонтального диска массой М = 200 кг и радиусом R = 1 м вращается вокруг вертикальной оси с частотой n = 6 об/мин. На краю платформы стоит человек массой m = 75 кг. Человек ловит мяч массой m0 = 1 кг, летящий горизонтально со скоростью υ = 5 м/с на расстоянии, равном радиусу платформы, от ее центра. С какой угловой скоростью ω будет вращаться платформа? Рассмотреть два случая направления движения мяча (по направлению движения платформы и в противоположном направлении).
задача 22895
На рисунке стрелками показаны направления углового ускорения вращающихся дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Какой из дисков вращается против часовой стрелки (если смотреть сверху)?
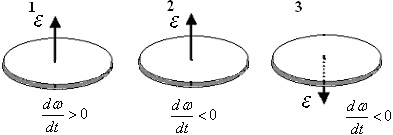
задача 22896
На рисунке стрелками показаны направления углового ускорения вращающихся дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Какие из дисков вращаются против часовой стрелки (если смотреть сверху)?
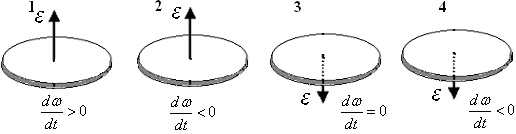
задача 23397
На рисунке дан график зависимости энергии вращающегося тела Wвр от угловой скорости. Чему будет равен момент импульса тела, при величине угловой скорости равной ω = 3 рад/с?
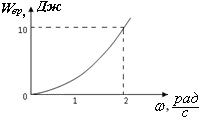
задача 23703
Тело вращается вокруг неподвижной оси по закону φ = At – Bt2, где A = 10 рад/с, В = 2,0 рад/с2. Через какое время тело остановится и сколько оборотов сделает до остановки?
задача 24008
Определить среднее угловое ускорение маховика, угловая скорость которого за время 18 полных оборотов возросла от частоты 7 оборотов в секунду до 17 оборотов в секунду.
задача 24046
Шар радиусом R = 0,20 м и массой m = 10 кг вращается вокруг оси, проходящей через его центр. По какому закону меняется момент силы и момент импульса шара, если угловое ускорение шара меняется со временем по закону ε = A·t, c–2, где А = 2 с–3. В начальный момент времени (t = 0) шар покоился.
задача 24518
Однородный стержень длиной l = 1,2 м и массой m = 0,3 кг вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через один из его концов с угловым ускорением ε = 9,81 с–1. Сколько оборотов сделает стержень за время t = 5,0 с, если он начал вращаться из состояния покоя? Как изменится вращающий момент, если ось вращения переместить в центр масс стержня, а действующая сила не изменяется?
задача 24531
Сфера радиусом R = 2,0 м равномерно вращается вокруг вертикального диаметра с частотой n = 60 об/мин. Внутри сферы находится шарик массой m = 0,3 кг. Найти высоту h, соответствующую положению равновесия шарика относительно дна сферы, и реакцию сферы N.
задача 24586
Человек массой 80 кг стоит на краю неподвижной платформы, представляющей собой однородный сплошной цилиндр массой 100 кг и радиусом 2 м, который может вращаться без трения вокруг вертикальной оси. С какой угловой скоростью начнет вращаться платформа после того как человек поймает мяч массой 0,5 кг, летящий горизонтально по касательной к платформе со скоростью 10 м/с. Человека рассматривать как материальную точку.
задача 24587
В результате взрыва звезда, вращавшаяся вокруг своей оси, увеличила объем в 8 раз. Считая звезду однородным шаром, определить каким стал период ее вращения, если до взрыва он был равен 1 месяцу?
задача 24609
Нормальное ускорение точки М диска, вращающегося вокруг неподвижной оси, равно 6,4 м/с2. Определить угловую скорость ω этого диска, если его радиус R = 0,4 м.
задача 24720
На графике представлена зависимость угла φ поворота вращающегося тела от времени t. Определите начальную угловую скорость вращения тела.
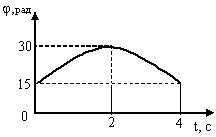
задача 24721
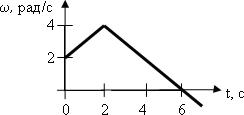
Тело вращается вокруг неподвижной оси. Зависимость угловой скорости от времени ω(t) показана на рисунке. Напишите уравнение φ = f(t), отражающее зависимость угла поворота тела от времени, если начальное положение тела соответствует значению φ0 = 2 рад.
задача 24754
Платформа в виде диска диаметром D = 4 м и массой m1 = 200 кг вращается вокруг вертикальной оси . С какой угловой скоростью ω1 будет вращаться эта платформа, если по ее краю пройдет человек массой m2 = 65 кг со скоростью v = 1,5 м/с относительно платформы?
задача 24962
Сплошной металлический цилиндр радиуса R вращается с постоянной угловой скоростью ω. Найдите зависимость напряженности поля Е от расстояния r от оси цилиндра и разность потенциалов U между поверхностью цилиндра и его осью.
задача 24970
Однородный диск радиуса 0,2 м и массы 5 кг вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени дается уравнением ω(t) = 0,5 + 8t, рад/с. Найти величину касательной силы, образующей крутящий момент.
задача 24991
Между зубчатыми колесами радиусами R и r находится в зацеплении ролик (рис. 1.14). Колеса начинают вращаться в противоположные стороны с угловыми скоростями ω1 и ω2. Какова будет угловая скорость вращения ролика вокруг собственной оси? Куда и с какой скоростью будет двигаться ось ролика? Решите задачу при условии, что колеса вращаются в одну сторону.
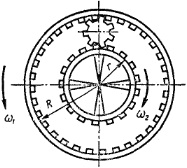
задача 25040
Однородный диск радиуса R = 80 см может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через точку О на нем, отстоящую на расстояние a = R/2 от центра диска. Диск отклонили от положения равновесия на угол α = 30° и отпустили. Определите: а) начальные угловое ускорение диска ε и тангенциальное ускорение aτс его центра масс С, б) угловую ω и линейную скорости vc центра масс диска при прохождении им положения равновесия.
задача 25041
Однородный диск радиуса R = 40 см может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через точку О на нем, отстоящую на расстояние a = R/4 от центра диска. Диск отклонили от положения равновесия на угол α = 50° и отпустили. Определите: а) начальные угловое ускорение диска ε и тангенциальное ускорение aτс его центра масс С, б) угловую ω и линейную скорости vc центра масс диска при прохождении им положения равновесия.
задача 25042
Однородный диск радиуса R = 40 см может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через точку О на нем, отстоящую на расстояние a = R/2 от центра диска. Диск отклонили от положения равновесия на угол α = 25° и отпустили. Определите: а) начальные угловое ускорение диска ε и тангенциальное ускорение aτс его центра масс С, б) угловую ω и линейную скорости vc центра масс диска при прохождении им положения равновесия.
задача 25961
Горизонтальная платформа массой 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, делая 10 об/мин. Человек весом 60 кг стоит при этом на краю платформы. С какой скоростью начнет вращаться платформа, если человек перейдет к ее центру? Считать платформу круглым однородным диском, а человека — точечной массой.
задача 26355
На краю круглой горизонтальной платформы радиусом R = 0,40 м стоит человек. Платформа вместе с ним вращается с угловой скоростью ω0 = 25,0 рад/с вокруг вертикальной оси, проходящей через центр тяжести платформы. В некоторый момент времени человек начинает идти вдоль края платформы со скоростью vч = 1,80 м/с (по отношению к платформе) в противоположную сторону ее вращения. Найти изменившуюся скорость платформы ωч , если ее масса M = 200 кг, а масса человека m = 70,0 кг.
задача 26401
Горизонтальная платформа массой m = 30 кг со стоящим на ее краю человеком вращается с частотой n1 = 5 об/мин вокруг вертикальной оси, проходящей через ее центр. С какой частотой начнет вращаться платформа, если человек массой m1 = 60 кг перейдет от края платформы к ее центру? Считать человека материальной точкой, а платформу–однородным диском.
задача 26417
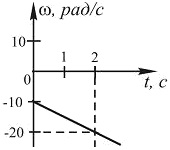
По приведенному графику построить графики зависимости углового ускорения и углового пути от времени, учитывая, что φ(0) = 0. Определить число оборотов, сделанное вращающимся телом за первые 6 с движения.
задача 26440
Обруч радиусом r = 0,5 м и массой m = 1 кг может вращаться вокруг горизонтальной оси (точка О). Его отклонили из положения равновесия на угол 90° и отпустили. Определить постоянный момент силы трения, который ось прикладывает к обручу, если при прохождении положения равновесия угловая скорость обруча ω = 4 рад/с.
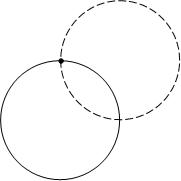
задача 26490
Гирька лежит на вращающемся относительно вертикальной оси диске. На каком расстоянии от оси лежит гирька, если диск вращается с угловой скоростью 10 рад/с? Коэффициент трения между диском и гирькой равен 0,1.
Задача 26585
Катушка вращается вокруг оси OO1 с угловой скоростью ω = 2 рад/с. Вдоль катушки перемещается точка М по закону М0М = 0,04t2. Определить абсолютное ускорение точки M, если радиус r = 0,02 м.
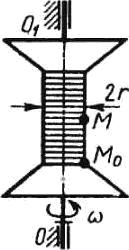
Задача 26586
По стороне треугольника, вращающегося вокруг стороны АВ с постоянной угловой скоростью ω = 4 рад/с, движется точка М с относительной скоростью vr. В момент времени, когда расстояние МВ = 0,5 м, определить модуль переносного ускорения точки M, если угол α = 30°.
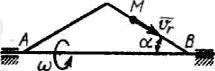
Задача 26599
Резервуар 1, момент инерции которого относительно вертикальной оси ?z равен 1 кг·м2, вращается с угловой скоростью ω0 = 18 рад/с. После открытия задвижки 2 он заполняется сыпучим материалом. Определить угловую скорость заполненного резервуара, если его момент инерции равен 3 кг·м2.
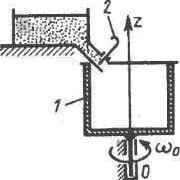
Задача 26602
К диску, который вращается вокруг оси О, прижимаются две тормозные колодки с силами F1 = F2 = 100 Н. Вычислить работу сил трения скольжения при торможении диска радиуса г = 0,1 м за 10 оборотов. Коэффициент трения скольжения тормозной колодки о диск / = 0,3.
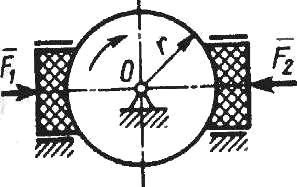
Задача 26615
Какую начальную угловую скорость ω0 надо сообщить однородному стержню длиной l = 3 м, чтобы он, вращаясь вокруг горизонтальной оси О, сделал пол-оборота?
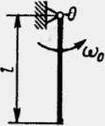
задача 26625
Определить модуль постоянного момента М пары сил, при действии которой барабан I вращается с угловым ускорением ε = 1 рад/с2. Барабан 1 и каток 2 — однородные цилиндры одинакового радиуса r = 0,2 м, массы тел m1 = m2 = 2 кг.
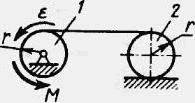
задача 26665
Платформа в виде диска радиусом R = 1 м вращается по инерции с частотой n1 = 6 об/мин. На краю платформы стоит человек, масса которого m = 88 кг. С какой частотой будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы J = 120 кг·м2. Момент инерции человека рассчитывать, как для материальной точки.
задача 26692
Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Угол поворота изменяется во времени по закону φ = А + Вt2 + Сt3, где А = 5 рад; B = 4 рад/c2 ; C = -1 рад/c3. Определить величину момента сил, приложенных к шару в момент времени 2 с.
задача 40490
Ha два взаимно перпендикулярных стержня, образующих крестовину, надеты четыре шара массой 30 г и радиусом 2,5 с . .  да шары находятся на расстоянии 10 с да шары находятся на расстоянии 10 с о о оси вращения, проходящей через центр крестовины, система вращается c частотой 3 об/с. C какой частотой станет вращаться данная система, оси вращения, проходящей через центр крестовины, система вращается c частотой 3 об/с. C какой частотой станет вращаться данная система,  ли ли  о о  я вращения шары переместятся на края стержней. Длина каждого стержня 30 с я вращения шары переместятся на края стержней. Длина каждого стержня 30 с , масса 150 г. , масса 150 г.
задача 40496
Ha верхней поверхности горизонтального диска, который  же же вращаться вокруг вертикальной оси, проложены вращаться вокруг вертикальной оси, проложены  о окружности радиусом 50 с о окружности радиусом 50 с рельсы игрушечной железной дороги. Масса диска 10 к рельсы игрушечной железной дороги. Масса диска 10 к , ,  о радиус 60 с о радиус 60 с . Ha рельсы неподвижного диска был поставлен заводной паровозик массой 1 к . Ha рельсы неподвижного диска был поставлен заводной паровозик массой 1 к и выпущен и и выпущен и рук. Он начал двигаться относительно рельсов со скоростью 0,8 м/с. C какой угловой скоростью будет вращаться диск? рук. Он начал двигаться относительно рельсов со скоростью 0,8 м/с. C какой угловой скоростью будет вращаться диск?
задача 40521
Космонавт, масса которого m = 75 кг, находится в центрифуге, вращающейся вокруг вертикальной оси с угловой скоростью ω = 4,33 рад/с. Радиус центрифуги R = 3 м. Определить числовое значение и направление веса Р космонавта.
задача 40522
Шар, радиус которого R = 0,1 м и масса m = 10 кг, вращается вокруг своей оси согласно уравнению φ = Аt3 + Bt2 + С, где А = 1 рад/с3, В = –3 рад/с2. Определить момент силы М для моментов времени t1 = 1 с и t2 = 2 с.
задача 40741
Угловая скорость вращающегося тела изменяется  о закону ω = 2t + 3t2. Ha какой угол повернулось тело о закону ω = 2t + 3t2. Ha какой угол повернулось тело  a время от t1 = 1 с до t2 = 3 с? a время от t1 = 1 с до t2 = 3 с?
задача 40811
Диск радиусом R вращается с угловой скоростью ω = 2 – 2t. Чему равно угловое ускорение диска? Как направлены вектора угловой скорости и углового ускорения? Сделать чертёж. Ось вращения проходит через центр диска.
задача 40813
Тело вращается вокруг неподвижной оси. Угловое ускорение ε = –3 с–2. Начальное значение угловой скорости 30 с–1. Записать закон изменения угловой скорости. Показать на рисунке, как направлены вектора 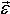 и и 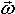 . .
задача 40858
Шар радиусом 10 см и массой 5 кг вращается вокруг оси симметрии по закону φ = A + Bt2 + Ct3, где В = 2 рад/с2, С = –0,5 рад/с3. Определить момент сил относительно оси вращения для момента времени t = 3 c.
|

 же
же вращаться вокруг вертикальной оси. С как
вращаться вокруг вертикальной оси. С как угловой скоростью будет вращаться
угловой скоростью будет вращаться  та платформа, если
та платформа, если  о ee краю пойдет человек массой m2 = 70 к
о ee краю пойдет человек массой m2 = 70 к со скоростью v = 1,8 м/с относительно платформы?
со скоростью v = 1,8 м/с относительно платформы?
 о инерции вокруг вертикальной оси c частотой n1 = 8 мин–1, стоит человек массой m1 = 70 к
о инерции вокруг вертикальной оси c частотой n1 = 8 мин–1, стоит человек массой m1 = 70 к .
.  да человек перешел в центр платформы,
да человек перешел в центр платформы,  на стала вращаться c частотой n2 = 10 мин–1. О
на стала вращаться c частотой n2 = 10 мин–1. О ить массу m2 платформы. Момент инерции человека рассчитывать
ить массу m2 платформы. Момент инерции человека рассчитывать  к для материальной точки.
к для материальной точки.
 вращается вокруг вертикальной оси, проходящей чepeз центр платформы, c частотой n = 8 мин–1. Человек массой m2 = 70 к
вращается вокруг вертикальной оси, проходящей чepeз центр платформы, c частотой n = 8 мин–1. Человек массой m2 = 70 к стоит при
стоит при  том на краю платформы. C какой угловой скоростью ω начнет вращаться платформа,
том на краю платформы. C какой угловой скоростью ω начнет вращаться платформа,  ли человек перейдет о
ли человек перейдет о края платформы к ee центру? Считать платформу круглым, однородным диском, a человека — материальной точкой.
края платформы к ee центру? Считать платформу круглым, однородным диском, a человека — материальной точкой.
 о инерции c частотой n1 = 6 об/мин. Ha краю платформы стоит человек, масса которого m = 80 к
о инерции c частотой n1 = 6 об/мин. Ha краю платформы стоит человек, масса которого m = 80 к . C как
. C как частотой будет вращаться платформа,
частотой будет вращаться платформа, 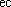 ли человек перейдет в ee центр? Момент инерции платформы J = 120 кг·м2. Момент инерции человека рассчитывать,
ли человек перейдет в ee центр? Момент инерции платформы J = 120 кг·м2. Момент инерции человека рассчитывать,  к для материальной точки.
к для материальной точки.

 и массой m = 5 к
и массой m = 5 к вращается вокруг оси симметрии согласно уравнению φ = А + Вt² + Сt³ (В = 2 рад/с², С = −0,5 рад/с³). О
вращается вокруг оси симметрии согласно уравнению φ = А + Вt² + Сt³ (В = 2 рад/с², С = −0,5 рад/с³). О и
и , стоящий на краю горизонтальной платформы массой М = 120 к
, стоящий на краю горизонтальной платформы массой М = 120 к , вращающейся
, вращающейся  о инерции вокруг неподвижной вертикальной оси c частотой n1 = 10 мин−1, переходит к ee центру. Считая платформу круглым однородным диском, a человека - точечной массой, определите, c как
о инерции вокруг неподвижной вертикальной оси c частотой n1 = 10 мин−1, переходит к ee центру. Считая платформу круглым однородным диском, a человека - точечной массой, определите, c как частотой n2 будет тогда вращаться платформа.
частотой n2 будет тогда вращаться платформа.
 друга на расстоянии R. Определите угловую скорость вращения, c которой
друга на расстоянии R. Определите угловую скорость вращения, c которой  ни должны вращаться вокруг общего центра масс,
ни должны вращаться вокруг общего центра масс,  бы расстояние между ними осталось постоянным.
бы расстояние между ними осталось постоянным.
























 .
.  да шары находятся на расстоянии 10 с
да шары находятся на расстоянии 10 с о
о оси вращения, проходящей через центр крестовины, система вращается c частотой 3 об/с. C какой частотой станет вращаться данная система,
оси вращения, проходящей через центр крестовины, система вращается c частотой 3 об/с. C какой частотой станет вращаться данная система,  ли
ли  о
о  я вращения шары переместятся на края стержней. Длина каждого стержня 30 с
я вращения шары переместятся на края стержней. Длина каждого стержня 30 с , масса 150 г.
, масса 150 г.
 же
же вращаться вокруг вертикальной оси, проложены
вращаться вокруг вертикальной оси, проложены  о окружности радиусом 50 с
о окружности радиусом 50 с рельсы игрушечной железной дороги. Масса диска 10 к
рельсы игрушечной железной дороги. Масса диска 10 к ,
,  о радиус 60 с
о радиус 60 с . Ha рельсы неподвижного диска был поставлен заводной паровозик массой 1 к
. Ha рельсы неподвижного диска был поставлен заводной паровозик массой 1 к и выпущен и
и выпущен и рук. Он начал двигаться относительно рельсов со скоростью 0,8 м/с. C какой угловой скоростью будет вращаться диск?
рук. Он начал двигаться относительно рельсов со скоростью 0,8 м/с. C какой угловой скоростью будет вращаться диск?
 о закону ω = 2t + 3t2. Ha какой угол повернулось тело
о закону ω = 2t + 3t2. Ha какой угол повернулось тело  a время от t1 = 1 с до t2 = 3 с?
a время от t1 = 1 с до t2 = 3 с?
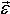 и
и 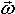 .
.