Физика и др.
Заказать решения

Задачи по физике (рус)

Задачі з фізики (укр)

Вопросы по физике:
6 класс

Другие предметы

Витамины для ума

Лучшая книга о разуме

кинематический ось ускорение точка определить материал уравнение движения скорость момент времени где

задача 10502

Движения двух материальных точек выражаются уравнениями x1 = A1 + В1t + С1t2 и x2 = A2 + В2t + С2t2 где A1 = 20 м; В1 = 2 м/с; С1 = –4 м/с2; A2 = 2 м; B2 = 2 м/с; С2 = 0,5 м/с2. В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения точек в этот момент?
Решение

задача 10988

Движение материальной точки задано уравнением x = At+Bt2, где A = 4 м/с, В = -0,05 м/с2. Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени.
Решение

задача 10993

Движения двух материальных точек выражаются уравнениями: x1 = A1+B1t+C1t2, x2 = A2+B2t+C2t2, где A1 = 20 м, A2 = 2 м, B1 = B2 = 2 м/с, C1 = -4 м/с2, С2 = 0,5 м/с2. В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v1 и v2 и ускорения a1 и а2 точек в этот момент.
Решение

задача 11015

Точка А движется с постоянной скоростью v по окружности радиусом R. Начальное положение точки и направление движения показаны на рисунке. Напишите кинематическое уравнение движения проекции точки A на направление оси х.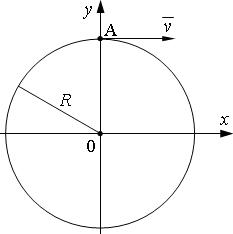
Решение

задача 11017

Написать для четырех случаев, представленных на рисунке: 1) кинематические уравнения движения x = f1(t) и x = f2(t); 2) уравнение траектории у = φ(х). На каждой позиции рисунка — а, б, в, г — изображены координатные оси, указаны начальное положение точки A, ее начальная скорость v0 и ускорение g.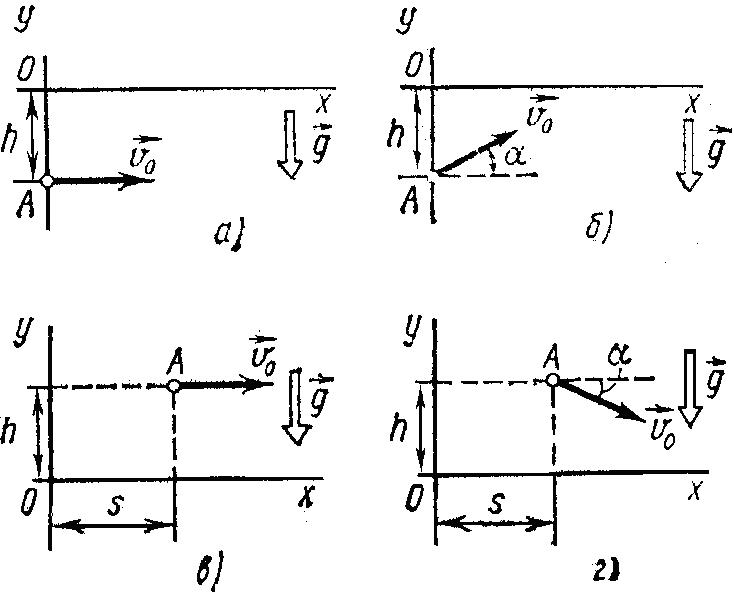
Решение

задача 12264

Кинематические уравнения двух материальных точек имеют вид x1 = A1t + B1t2 + C1t3 и x2 = A2t + B2t2 + C2t3, где B1 = 4 м/с2, C1 = –3 м/с, B2 = 4 м/с, C2 = 1 м/с3. Определить момент времени, для которого ускорения этих точек будут равны.
Решение

задача 13016

Кинематические уравнения движения двух материальных точек имеют вид х1 = A1t + B1t² + С1t³ и х2 = A2t + В2t² + C2t³, где В1 = 4 м/с², С1 = −3 м/с³, В1 = −2 м/с², С2 = 1 м/с³. Определите момент времени, для которого ускорения этих точек будут равны.
Решение

Задача 23961

В таблице приведены уравнения изменения со временем кинематических характеристик вращающегося маховика, закрепленного на валу двигателя. 1. Постройте графики изменения со временем угла поворота φ(t), угловой скорости ω(t) и углового ускорения β(t). Поясните характер движения вала. 2. Определите полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вала в момент времени t = 10 с. Угол поворота задан в радианах, А = 0,0314 рад/с2, B = 0,1 рад/с. β = –Acos Bt, φ(0) = 0, ω(0) = 0,1π рад/с.
Решение

Задача 26580

Даны уравнения движения точки: х = 0,01t3, у = 200 – 10t. Определить ускорение в момент времени, когда точка пересекает ось Ох.
Решение

Задача 26581

Даны уравнения движения точки: х = 8 – t2, у = t2 – cos t. Определить проекцию ускорения ау в момент времени, когда координата x = 0.
Решение

Задача 26595

Материальная точка массой т = 0,5 кг движется согласно векторному уравнению r = 2 sin πti + 3 cos пtj. Определить проекцию количества движения точки на ось Ох в момент времени t = 0,5 с.
Решение

Задача 26596

Определить проекцию на ось Оу главного вектора количества движения системы двух материальных точек, массы которых m1 = 4 кг, m2 = 2 кг, в момент времени, когда их скорости v1 = 2 м/с, v2 = 1 м/с.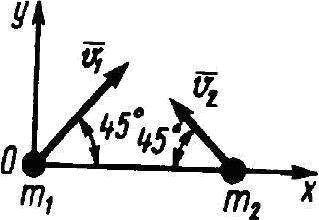
Решение

Задача 26612

Груз массою m = 4 кг, опускаясь вниз, приводит с помощью нити во вращение цилиндр радиуса R = 0,4 м. Момент инерции цилиндра относительно оси вращения I = 0,2 кг·м2. Определить кинематическую энергию системы тел в момент времени, когда скорость груза v = 2 м/с.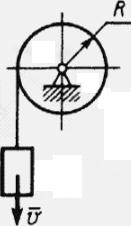
Решение

задача 13302

Кинематические уравнения движения двух материальных точек имеют вид х1 = А1+B1t+С1t2 и х2 = А2+В2t+C2t2, где (пропущено в книге: B1 = B2), C1 = –2 м/c2, С2 = 1 м/с2. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а1 и а2 для этого момента.
Решение

задача 13303

Радиус-вектор материальной точки изменяется со временем по закону r = t3i+3t2j, где i, j — орты осей х и у. Определите для момента времени t = 1 с: 1) модуль скорости; 2) модуль ускорения.
Решение

задача 13787

Зависимость скорости материальной точки от времени задана уравнением v = 5t3 + 3t2 + 2 (м/с). Найти ускорение в момент времени 1 с и путь, пройденный точкой за 2 с.
Решение

задача 15168

Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct3, где А = 2 м, В = 1 м/с, С = –0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
Решение

задача 15175

Уравнение движения материальной точки вдоль оси имеет вид х = А – Bt + Ct3, где А = 2 м, В = 2 м/с, С = –0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
Решение

задача 15182

Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct3, где А = 2 м, В = 2 м/с, С = –1,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
Решение

задача 15192

Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt – Ct3, где А = 2,1 м, В = 1 м/с, С = –0,8 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
Решение

задача 15199

Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct3, где А = 1 м, В = 2 м/с, С = 0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
Решение

задача 15206

Уравнение движения материальной точки вдоль оси имеет вид х = А – Bt – Ct3, где А = 2 м, В = 1 м/с, С = 0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 4 с.
Решение

задача 15213

Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct3, где А = 2 м, В = –1 м/с, С = –0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 10 с.
Решение

задача 15221

Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct2, где А = 2 м, В = 1 м/с, С = –0,5 м/с2. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
Решение

задача 15228

Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct2, где А = –2 м, В = 1 м/с, С = 1,5 м/с2. Найти координату х, скорость vx и ускорение ах в момент времени τ = 20 с.
Решение

задача 15233

Уравнение движения материальной точки вдоль оси имеет вид х = А – Bt – Ct3, где А = 2 м, В = –1 м/с, С = 0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
Решение

задача 16072

Материальная точка на плоскости совершает движение, которое задается кинематическими уравнениями: х = A·cos(ω·t); у = B·cos(ω·t + φ0), где х и у — координаты точки в момент времени t, А = 4 м, В = 8 м, φ0 = π, ω = π рад/с. Определить траекторию точки и скорость точки в момент времени t1 = 1 с.
Решение

задача 16474

Кинематическое уравнение движения материальной точки вдоль прямой (ось ОХ) задается уравнением х = A + Bt + Сt2 + Dt3, где B = 8 м/с; С = –4 м/с2; D = 1,5 м/с3. Определите среднюю скорость и среднее ускорение материальной точки за промежуток времени, в течение которого точка движется в направлении, противоположном первоначальному.
Решение

задача 17142

Движения двух материальных точек задаются уравнениями v1(t) = B1t + C1t2, х2(t) = B2t2 + C2t3, где B1 = 8 м/с,
Решение

задача 17418

Движение материальной точки задано уравнением: x = A+Bt2, где А = 4 м/с, В = –0,05 м/с2. Определить момент времени, в который скорость точки v = 0. Найти координату и ускорение точки в этот момент.
Решение

задача 19502

Две материальные точки движутся вдоль одной прямой с ускорениями a1 = A1+B1t, a2 = A2+B2t, где A1 = 4 м/c2, B1 = 3 м/с3, A2 = 12 м/с2, B2 = –1 м/с3. Начальные скорости этих точек были равны, соответственно, 8 м/с и 12,5 м/с. В какой момент времени t скорости точек будут одинаковы?
Решение

задача 19586

Кинематические уравнения движения двух материальных точек имеют вид: x1 = A1t + B1t2 + С1t3 и x2 = A2t + B2t2 + C2t3, где B1 = 2 м/с2, C1 = –1,5 м/с3, B2 = –1 м/с2; C2 = 0,5 м/с3. Определите, в какой момент времени ускорения этих точек одинаковы.
Решение

задача 19741

Скорость движения точки v = 4,9ti + 7,6j м/с. Определите угол между вектором скорости и осью OX в момент времени t = 0,1 c.
Решение

задача 19821

Материальная точка вращается вокруг неподвижной оси по закону φ = A+Bt+Ct2, где A = 10 рад, B = 20 рад/с, C = –2 рад/с2 . Найти полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вращения, для момента времени t = 4 с.
Решение

задача 19823

Материальная точка движется по закону: Y(t) = At+Ct2+Bt4, где A = 6 м/с, C = 0,2 м/с2, B = –0,125 м/с4 . Найти скорость и ускорение точки в моменты времени t1 = 0 c и t2 = 2 с, а также среднюю скорость перемещения и среднее ускорение за первые 2 с движения.
Решение

задача 19824

Материальная точка вращается вокруг неподвижной оси по закону φ = A+Ct2+Bt3, где A = 10 рад, B = 0,5 рад/с3, C = –2 рад/с2 . Найти полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вращения, для момента времени t = 3 с.
Решение

задача 20080

Материальная точка совершает колебательное движение вдоль оси ОХ по закону X = 8cos(πt+π/2), см. Найти период колебаний и ускорение точки в момент t = T/2, построить график зависимости x(t).
Решение

задача 20190

Ускорение материальной точки (М.Т.) изменяется по закону: a = 1+2t м/с2. Определить зависимость x(t), если в начальный момент времени М.Т. находилась в точке с координатой х0 = 5 м и имела скорость v0 = 3 м/с.
Решение

задача 20191

Ускорение материальной точки (М.Т.) изменяется по закону: a = 1+t2 м/с2. Определить зависимость x(t), если в начальный момент времени М.Т. находилась в точке с координатой х0 = 3 м и имела скорость v0 = 1 м/с.
Решение

задача 20192

Ускорение материальной точки (М.Т.) изменяется по закону: a = 2+t м/с2. Определить зависимость x(t), если в начальный момент времени М.Т. находилась в точке с координатой х0 = 3 м и имела скорость v0 = 5 м/с.
Решение

задача 20194

Ускорение материальной точки (М.Т.) изменяется по закону: a = 1+t м/с2. Определить зависимость x(t), если в начальный момент времени М.Т. находилась в точке с координатой х0 = 1 м и имела скорость v0 = 0 м/с.
Решение

задача 20210

В начальный момент времени две материальные точки находятся на некоторой высоте от поверхности земли в одной точке и обладают скоростями, соответственно равными v01 и v02 = 45,5 м/с, направленными горизонтально в противоположные стороны. Через время t = 10 с после начала одновременного движения векторы скоростей образуют между собой угол α = 45°, а расстояние между материальными точками становится равным l. Определить v01.
Решение

задача 20211

В начальный момент времени две материальные точки находятся на некоторой высоте от поверхности земли в одной точке и обладают скоростями, соответственно равными v01 = 9,3 м/с и v02, направленными горизонтально в противоположные стороны. Через время t = 4 с после начала одновременного движения векторы скоростей образуют между собой угол α = 60°, а расстояние между материальными точками становится равным l. Определить v02.
Решение

задача 20212

В начальный момент времени две материальные точки находятся на некоторой высоте от поверхности земли в одной точке и обладают скоростями, соответственно равными v01 = 24,0 м/с и v02 = 16,0 м/с, направленными горизонтально в противоположные стороны. Через время t = 6 с после начала одновременного движения векторы скоростей образуют между собой угол α, а расстояние между материальными точками становится равным l. Определить α.
Решение

задача 20213

В начальный момент времени две материальные точки находятся на некоторой высоте от поверхности земли в одной точке и обладают скоростями, соответственно равными v01 = 42,0 м/с и v02 = 68,8 м/с, направленными горизонтально в противоположные стороны. Через время t после начала одновременного движения векторы скоростей образуют между собой угол α = 90°, а расстояние между материальными точками становится равным l. Определить t.
Решение

задача 20214

В начальный момент времени две материальные точки находятся на некоторой высоте от поверхности земли в одной точке и обладают скоростями, соответственно равными v01 = 12,0 м/с и v02 = 5,0 м/с, направленными горизонтально в противоположные стороны. Через время t после начала одновременного движения векторы скоростей образуют между собой угол α = 90°, а расстояние между материальными точками становится равным l. Определить l.
Решение

задача 20791

Материальная точка совершает колебания по закону x(t) = Acos(ωt), где А = 4 см, ω = 2 рад/с. Определить величину скорости точки в тот момент времени, когда ее ускорение а = 2 см/с2.
Решение

задача 21030

Материальная точка массой m = 5 кг в начале движения по горизонтальной прямой малая скорость V0 = 3 м/с и на нее действовала сила F = 8 + 3t, которая направлена по той же прямой. Определить скорость точки в момент времени t1 = 4 с.
Решение

задача 21480

Зависимость координаты материальной точки от времени выражается уравнением: x(t) = 1,5t2–0,25t3, м. Вычислите: 1) зависимость скорости и ускорения от времени; 2) скорость и ускорение в момент времени t = 1 c; 3) максимальную скорость точки; 4) перемещение через 3 с от начала движения; 5) постройте графики зависимостей: x = f(t), v = f(t), a = f(t); 6) назовите характер движения тела.
Решение

задача 21672

В таблице приведены уравнения изменения со временем кинематических характеристик вращающегося маховика, закрепленного на валу двигателя. 1. Постройте графики изменения со временем угла поворота φ(t), угловой скорости ω(t) и углового ускорения β(t). Поясните характер движения вала. 2. Определите полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вала в момент времени t = 10 с. Угол поворота задан в радианах, А = 0,0314 рад/с2, B = 0,1 рад/с. β = Ae–Bt, φ(0) = 0, ω(0) = 0.
Решение

задача 21832

Движение тела в поле Земли определяется уравнениями х(t) = 15t, y(t) = 30t–4,9t2, м. Вычислите:
1) зависимость проекций скорости и ускорения на оси OХ и OΥ от времени;
2) начальную и конечную скорости движения точки;
3) запишите уравнение траектории движения тела у = f(t), постройте график зависимости у = f(t) для моментов времени t1 = 0 с, t2 = tподъема, t3 = tпадения и назовите характер движения тела;
4) максимальную высоту подъема, дальность полета и модуль перемещения;
5) радиус кривизны в верхней точке траектории.
Решение

задача 21908

Материальная точка движется с ускорением, зависящим от времени a(t) = A–Bt, где А = 3 м/с2, В = 1 м/с3. Найти зависимость скорости и координаты от времени, если в начальный момент времени х0 = 0, v0 = 2 м/с. Найти путь, который пройдет точка до остановки.
Решение

задача 22108

Уравнение движения материальной точки имеет вид x = A + Bt + Ct2 + Dt3, где A = 6 м, B = 3 м/с, C = 2 м/с2, D = 1 м/с3. В интервале времени t1 = 1 с до t2 = 4 с найти: а) среднюю скорость; б) среднее ускорение движения точки.
Решение

задача 22882

Закон движения материальной точки имеет вид: r = 2ti + (2 + 3t2)j. Найдите проекции вектора скорости v на оси координат и запишите зависимость вектора скорости от времени. Вычислите величину ускорения через 2 с после начала движения.
Решение

задача 22933

Движение точки описывается уравнением S = 5t3–4t2+40 (в единицах СИ). Найдите скорость и ускорение точки в момент времени t1 = 2 c. Найдите путь, пройденный телом к моменту времени t2 = 3 c.
Решение

задача 23066

Уравнение движения частицы дано в виде x = sin(πt/6). Найти моменты времени t, в которые достигается максимальная скорость частицы.
Решение

задача 23267

Зависимость координаты материальной точки от времени выражается уравнением: х = 1,5t2 – 0,25t3, м. Определить: 1) зависимость скорости и ускорения от времени; 2) скорость и ускорение в момент времени t1 = 1 с; 3) максимальную скорость точки; 4) перемещение через 3 с от начала движения.
Решение

задача 23529

Зависимость координаты материальной точки от времени выражается уравнением: x = 3t2–0,5t3 (м). Вычислите: 1) зависимость скорости и ускорения от времени; 2) максимальную скорость движения точки, её перемещение через 2 с, а также скорость и ускорение в момент времени t1 = 1 с; 3) постройте графики зависимости x = f(t), v = f(t) и a = f(t) для моментов времени t = 0, 1, 2, 3, 4 c.
Решение

задача 23533

Материальная точка движется в поле Земли согласно уравнениям движения x(t) = 5t, y(t) = 10–4,9t2, м. Вычислите: 1) зависимость проекций скорости ускорения на оси OX и OY от времени; 2) время движения точки; 3) запишите уравнение траектории y = f(t) и определите характер движения точки; 4) начертите график зависимости y = f(t); 5) полное ускорение, начальную и конечную скорости движения, а также модуль перемещения.
Решение

задача 23535

Движение тела в поле Земли определяется уравнениями x(t) = 10t, y(t) = 20t–4,9t2, м. Вычислите: 1) зависимость проекций скорости и ускорения на оси OX и OY от времени; 2) начальную и конечную скорости движения; 3) уравнения траектории движения тела y = f(t) и постройте график зависимости y = f(t) для моментов времени t1 = 0 c, t2 = tподъема, t3 = tпадения, назовите характер движения тела. 4) максимальную высоту подъема, дальность полета и модуль перемещения; 5) радиус кривизны в верхней точке траектории.
Решение

задача 23586

В таблице приведены уравнения изменения со временем кинематических характеристик вращающегося маховика, закрепленного на валу двигателя. 1. Постройте графики изменения со временем угла поворота φ(t), угловой скорости ω(t) и углового ускорения β(t). Поясните характер движения вала. 2. Определите полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вала в момент времени t = 10 с. Угол поворота задан в радианах, А = 0,0314 рад/с2, B = 0,1 рад/с. β = –Asin Bt, φ(0) = 0, ω(0) = 0,1π рад/с.
Решение

задача 23975

Движение тела вдоль прямой описывается уравнением х = A+Вt+Ct2+Dt3, где A = 2 м. От момента времени t1 = 0,7 с до t2 = 11,0 с тело проходит путь s. Средняя скорость и среднее ускорение на этом интервале vs и as. v1 = 0,8 м/с, а1, v2 = 0,2 м/с, a2 — скорость и ускорение в моменты времени t1 и t2. Найти путь s и все скорости и ускорения (кроме заданных).
Решение

задача 23988

Точка движется по прямой согласно уравнению x = At + Bt3, где A = 6 м/с, В = –2 м/с3. Найти ускорение в момент, когда скорость равна нулю.
Решение

задача 23989

Движение точки по кривой задано уравнением r = iA1t3 + j(A2t2+B2t), где A1 = 1 м/с3, A2 = –1 м/с2 и B2 = 4 м/с. Найти скорость v в тот момент времени, когда она параллельна оси ОХ.
Решение

задача 24162

Координаты x и y материальной точки зависят от времени по законам x = A·cos ωt, y = B·sin ωt, где A, B, ω — постоянные величины. Найдите величину v скорости материальной точки в момент ωt = π/4.
Решение

задача 24511

Центрифуга, предназначенная для изучения действия ускорения на организм человека, делала 12 об/мин; затем в течение 5 с число оборотов центрифуги изменилось так, что на летчика стало действовать ускорение 10g. Определить угловое ускорение движения летчика, если кабина укреплена на расстоянии 7 м от оси вращения центрифуги.
Решение

задача 26683

Движение материальной точки задано уравнением x = At+Bt2, где A = 4 м/с, В = –0,05 м/с2. Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент.
Решение

задача 40005

Кинематическое уравнение движения материальной точки по прямой (ось x) имеет вид x = А+Bt+Сt2, где А = 5 м, В = 4 м/с, С = –1 м/с2. 1. Построить график зависимости координаты x и пути s от времени. 2. Определить среднюю скорость <vx> за интервал времени от t1 = 1 с до t2 = 6 с. 3. Найти среднюю путевую скорость <v> на тот же интервал времени.
Решение

задача 40797

Определить модуль ускорения точки в момент времени 1 с, если уравнение движения точки x = cos πt см, y = sin πt см.
Решение