найти результирующую амплитуду колебаний одинаковый фаза два
задача 10078
Складываются два колебания одинакового направления и одинакового периода: х1 = А1sinω1t и x2 = A2sinω2(t+τ), где А1 = A2 = 3 см, ω1 = ω2 = π c–1, τ = 0,5 c. Определить амплитуду А и начальную фазу φ0 результирующего колебания. Написать о уравнение. Построить векторную диаграмму для момента времени t = 0.
о уравнение. Построить векторную диаграмму для момента времени t = 0.
задача 10575
Складываются два колебания одинакового направления и одинакового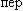 и
и да: х1 = А1sin ω1t и х2 = А2sin ω2(t+τ), где A1 = 1 см; ω1 = ω2 = π c–1; τ = 0,5 c. О
да: х1 = А1sin ω1t и х2 = А2sin ω2(t+τ), где A1 = 1 см; ω1 = ω2 = π c–1; τ = 0,5 c. О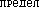 ить амплитуду A и начальную фазу φ0 результирующего колебания. Написать
ить амплитуду A и начальную фазу φ0 результирующего колебания. Написать  о уравнение.
о уравнение.
задача 11314
Определить амплитуду А и начальную фазу φ результирующего колебания, возникающего при сложении двух колебаний одинаковых направления и периода: x1 = A1sinωt и x2 = A2sinω(t+τ), где A1 = A2 = 1 см; ω = π с–1; τ = 0,5 с. Найти уравнение результирующего колебания.задача 11315
Точка участвует в двух одинаково направленных колебаниях: x1 = A1sinωt и x2 = A2cosωt, где А1 = 1 см; A2 = 2 см; ω = 1 с–1. Определить амплитуду А результирующего колебания, его частоту ν и начальную фазу φ. Найти уравнение этого движения.задача 12187
Точка участвует в двух одинаково направленных колебаниях х1 = А1·sin ωt и x2 = A2·sin ωt, где А1 = 1 см, A2 = 2 см, ω = 1 рад/с. Определить амплитуду результирующего колебания. Записать уравнение колебаний.задача 12468
Сложить два колебания: x1 = 5 cos14t и x2 = 4cos12t. Найти период биений и период результирующего колебания.задача 12876
Грузик, подвешенный на легкой пружине, совершает гармонические колебания в вертикальной плоскости с амплитудой 5 см. В некоторый момент точка подвеса сама начинает колебаться в вертикальной плоскости с амплитудой 5 см и тем же периодом. Найти разность фаз складываемых колебаний, если амплитуда результирующего колебания равна 10 см.задача 12983
Электростатическое поле создано в вакууме положительными точечными зарядами 2q и 3q. Найдите, как и во сколько раз изменится напряженность результирующего поля в точке А, лежащей посередине между зарядами, если заряд 2q заменить зарядом –2q.задача 12991
В вершинах прямоугольника со сторонами а = 6 см и b = 8 см расположены два положительных и два отрицательных точечных заряда, причем q1 = q2 = 2 нКл, q3 = q4 = –2 нКл. Найти напряженность результирующего поля в точке пересечения диагоналей прямоугольника.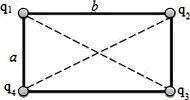
задача 13035
В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами и одинаковыми периодами получается результирующее колебание с тем же периодом и той же амплитудой. Найти разность фаз складываемых колебаний (в градусах).задача 13681
Складываются два гармонических колебания одного направления, описываемых уравнениями х1 = 3соs2πt, см х2 = 3 cos(2πt + π/4), см. Определите для результирующего колебания: 1) амплитуду; 2) начальную фазу. Запишите уравнение результирующего колебания и представьте векторную диаграмму сложения амплитуд.задача 13685
Складываются два гармонических колебания одного направления, имеющие одинаковые амплитуды и одинаковые начальные фазы, c периодами T1 = 2 c и Т2 = 2,05 c. Определите: 1)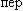 и
и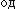 результирующего колебания; 2) период биения.
результирующего колебания; 2) период биения.
задача 14264
Запишите условие максимального усиления при наложении двух когерентных световых волн 1 и 2 через их разность фаз Δφ. Какое соотношение между интенсивностьюзадача 14623
Два точечных электрических заряда q1 = +5q и q2 = –2q находятся на расстоянии r = 10 см друг от друга. Найдите, на каком расстоянии x от заряда q1 напряженность Ex результирующего электростатического поля равна нулю.задача 14633
В вакууме на расстоянии r = 10 см друг от друга расположены два точечных заряда q1 = –10 нКл и q2 = 6 нКл. Расстояние АВ = 5 см, ε = 1. Чему равен потенциал результирующего поля в точке В?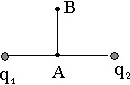
задача 15045
Амплитуда результирующего колебания, получающегося при сложении двух одинаково направленных гармонических колебаний одинаковой частоты, обладающих разностью фаз 60°, равна 6 см. Определить амплитуду второго колебания, если А1 = 5 см.задача 15177
В центр квадрата, в вершинах которого находится по заряду q = 1,2·10–9 Кл, помещен отрицательный заряд. Найти величину этого заряда Q, если результирующая сила F, действующая на каждый заряд q, равна нулю.задача 15184
В центр квадрата, в вершинах которого находится по заряду q = –2·10–9 Кл, помещен отрицательный заряд. Найти величину этого заряда Q, если результирующая сила F, действующая на каждый заряд q, равна нулю.задача 15208
В центр шестиугольника, в вершинах которого находится по заряду q = 2·10–9 Кл, помещен отрицательный заряд. Найти величину этого заряда Q, если результирующая сила F, действующая на каждый заряд q, равна нулю.задача 15501
Найти амплитуду А и начальную фазу φ гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями x1 = 4sin πt см и х2 = 3sin(πt+π/2) см. Написать уравнение результирующего колебания. Дать векторную диаграмму сложения амплитуд.задача 15506
Точка участвует в двух колебаниях одинакового периода с одинаковыми начальными фазами. Амплитуды колебаний равны A1 = 3 см и A2 = 4 см. Найти амплитуду А результирующего колебания, если колебания совершаются; а) в одном направлении; б) в двух взаимно перпендикулярных направлениях.задача 16076
Два заряда q и 2q закреплены на расстоянии 1 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд, чтобы результирующая сила, действующая на каждый заряд, равнялась нулю. Найти знак и величину этого заряда.задача 16130
Точка участвует в трех колебаниях, происходящих по одной прямой и выраженных уравнениями x1 = 3cost, x2 = 3cos(t+π/3), x3 = 3sin(t+7π/6) (смещения даны в см). Определить амплитуду и начальную фазу результирующего колебаний. Написать его уравнение движения.задача 16479
Три одинаковых заряда величиной q = 10 нКл расположены в вершинах правильного треугольника со стороной 1 см. Какой отрицательный заряд нужно поместить в центр треугольника, чтобы результирующая сила, действующая на каждый заряд, была равна нулю.задача 16489
Частица участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 4 Гц одинакова для обоих колебаний, начальные фазы имеют значения π/12 рад и 7π/12 рад, а амплитуды соответственно равны 5 см и 5 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания. Запишите уравнение для скорости результирующего колебания, если масса частицы 25 г.задача 16563
Сложить два колебания х1 = 2 cos 28t и х2 = 4 cos 26t. Найти период биений и период результирующего колебания.задача 16583
Используя векторную диаграмму, сложить 5 сонаправленных колебаний:x1 = 2·cos(ω·t), мм;
х2 = 2·sin(ω·t), мм;
x3 = 2·cos(ω·t + π/4), мм;
x4 = 2·cos(ω·t + 3π/4), мм;
x5 = 2·cos(ω·t + 5π/4), мм.
Записать уравнение результирующего колебания.
задача 17163
Точка участвует в двух взаимно перпендикулярных колебаниях х = 2sin(ωt) м и y = cos(ωt) м. Найдите траекторию результирующего движения точки.задача 17636
Написать уравнение результирующего колебания, полученного в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами ν = 5 Гц и с одинаковой начальной фазой ψ1 = ψ2 = π/3. Амплитуды колебаний равны А1 = 0,01 м и А2 = 0,05 м.задача 17919
Частица участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 8 Гц одинакова для обоих колебаний, начальные фазы имеют значения π/2 рад и π рад, а амплитуды соответственно равны 11 см и 11 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания. Запишите его уравнение.задача 17956
Частица участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 5 Гц одинакова для обоих колебаний, начальные фазы имеют значения π/6 рад и –π/6 рад, а амплитуды соответственно равны 8 см и 10 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания, запишите его уравнение и постройте график от времени.задача 17962
Используя векторную диаграмму, сложить 6 сонапрапленных колебаний:задача 17964
Частица участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 6 Гц одинакова для обоих колебаний, начальные фазы имеют значения 3π/4 ραд и 5π/4 рад, а амплитуды соответственно равны 6 см и 6 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания, запишите его уравнение.задача 17967
Частица участвует одновременно в двух гармонических колебаниях, совершающихся по взаимно перпендикулярным направлениям. Заданы частоты колебаний ν1 = 3 Гц, ν2 = 3 Гц, их амплитуды А1 = 4 А2 = 6 см и начальные фазы π/4 рад и 7π/12 рад. Напишите уравнения исходных колебаний. Найдите уравнение траектории результирующего движения в координатах XOY и постройте ее график. Укажите на графике положение частицы в начальный момент времени и направление движения по траектории.задача 17969
Частица участвует одновременно в двух гармонических колебаниях, совершающихся по взаимно перпендикулярным направлениям. Заданы частоты колебаний ν1 = 4 Гц и ν2 = 4 Гц. Их амплитуда А1 = 5 см, А2 = 8 см и начальные фазы π/2 рад и π/2 рад. Напишите уравнения исходных колебаний. Найдите уравнение траектории результирующего движения в координатахзадача 17975
При помощи векторной диаграммы сложить 3 сонаправленных колебания: х1 = 3·cos(ω·t), см; x2 = 3·sin(ω·t), см; х3 = 6·sin(ω·t + π), см. Записать уравнение результирующего колебания, если ω = π/2 рад/с. Построить график зависимости хрез от времени.задача 17979
При сложении гармонических колебаний с близкими частотами уравнение результирующих колебаний (биений) имеет вид: х = 10·cos(4t)·cos(104t) мм. Определить частоты складываемых колебаний и записать уравнения этих колебаний.задача 17980
При сложении гармонических колебаний с близкими частотами уравнение результирующих колебаний имеет вид: х = 10·cos(4t)·cos(104t) мм. Определить частоты складываемых колебаний и записать уравнения этих колебаний. Сколько колебаний совершает колеблющаяся точка за время, равное периоду биений?задача 18216
Две плоские синусоидальные волны, амплитуды которых одинаковы, а частоты соответственно ν и ν+Δν (Δν << ν), накладываются друг на друга. Какова максимальная амплитуда результирующей волны? Каково распределение средней плотности энергии вдоль направления распространения волны?задача 19164
Найти амплитуду и начальную фазу α колебаний, получающихся в результате сложения следующих колебаний одного направления: x1 = 20 cos ωt (мм), x2 = 20 cos(ωt + π/3) (мм), где ω = π с–1. Написать уравнение результирующих колебаний x(t).задача 19168
Частица участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 3 Гц одинакова для обоих колебаний, начальные фазы имеют значения 3π/4 рад и π рад, а амплитуды соответственно равны 7 см и 4 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания. Запишите его уравнение. Найдите энергию частицы, если ее масса 15 г.задача 19180
Частица участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 5 Гц одинакова для обоих колебаний, начальные фазы имеют значения π/6 рад и –π/6 рад, а амплитуды соответственно равны 8 см и 10 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания. Запишите его уравнение. Найдите уравнение скорости результирующего движения.задача 19190
Частица участвует одновременно в двух гармонических колебаниях, совершающихся по взаимно перпендикулярным направлениям. Заданы частоты колебаний ν1 = 14 Гц, ν2 = 14 Гц, их амплитуды А1 = 15 см, А2 = 20 см и начальные фазы π/2 рад и π/4 рад. Напишите уравнения исходных колебаний. Найдите уравнение траектории результирующего движения в координатах ХОУ и постройте ее график. Укажите на графике положение частицы в начальный момент времени и направление движения по траектории.задача 19254
Частица участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 2 Гц одинакова для обоих колебаний, начальные фазы имеют значения 4π/3 рад и 2π/3 рад, а амплитуды соответственно равны 7 см и 4 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания. Запишите его уравнение. Найдите период результирующих колебаний.задача 19620
Используя векторную диаграмму, сложить 6 сонапрапленных колебаний:x1 = 3·cos(ω·t);
x2 = 3·cos(ω·t + π/2);
x3 = 4·cos(ω·t – π/2);
x4 = 4·cos(ω·t + π);
x5 = sin(ω·t);
x6 = sin(ω·t + π/2).
Записать уравнение результирующего колебания (x1, x2 ..., x6 измеряются в см).
задача 19960
Написать уравнение движения, получающегося в результате сложения двух одинаково направленных гармонических колебаний, заданных уравнениями х1 = 4sinπt см и х2 = 3sin(πt+π/3) см. Написать уравнение результирующего колебания. Построить векторную диаграмму сложения амплитуд.задача 20381
Материальная точка участвует одновременно в двух колебаниях одного направления x1 = 5 sin (2t + π/4), см и х2 = 15 sin 2t, см. Записать уравнение результирующего колебания. Определить скорость точки через 0,2 с.задача 20382
Складываются два колебания одного направления, происходящие по закону косинуса, с одинаковыми амплитудами 0,1 м и одинаковыми начальными фазами, частоты которых равны 50 и 50,6 Гц. Записать уравнение результирующего колебания.задача 20563
Складываются два колебания одинакового направления и одинаковой частоты. Законы колебаний имеют вид: x1(t) = 3cos(5πt + π/6), x2(t) = 2sin(5πt – 2π/3). Определить амплитуду, период и начальную фазу результирующего колебания. Записать закон результирующего колебания, изобразить колебания в виде векторов на координатной плоскости.задача 20696
Складываются два колебания одинакового направления и одинаковой частоты. Законы колебаний имеют вид: x1(t) = sin(πt + π/4), x2(t) = 3sin(πt + π/6). Определить амплитуду, период и начальную фазу результирующего колебания. Записать закон результирующего колебания, изобразить колебания в виде векторов на координатной плоскости.задача 20812
Складываются два гармонических колебания, происходящих в одном направлении: x1 = 2cos2πt см и x2 = 2cos(2πt+π/3) см. Напишите уравнение результирующего колебания и постройте векторную диаграмму сложения амплитуд.задача 20824
Складываются три гармонических колебания одного направления с одинаковыми периодами. Амплитуды и начальные фазы колебаний равны: А1 = 3 см, φ1 = 0; А2 = 1 см, φ2 = π/2 ; А3 = 2 см, φ3 = π. Построить векторную диаграмму сложения амплитуд, определить амплитуду и фазу результирующего колебания и записать его уравнение.задача 21126
Складываются два колебания одного направления и периода. Амплитуды складываемых колебаний: A1 = 2 см, А2 = 4 см. Начальные фазы колебаний φ1 = 30°, φ2 = 60°. Определить амплитуду и начальную фазу результирующего колебания. Построить векторную диаграмму.задача 21159
Амплитуды и периоды двух одинаково направленных гармонических колебаний равны, фазы же различаются на 2π/3. Уравнение результирующего колебания в единицах СИ имеет вид x = 0,2cos(πt+π). Определить уравнения слагаемых колебаний.задача 21426
Материальная точка участвует в двух колебаниях, происходящих по одной прямой и выражаемых уравнениями x1 = cos t см и х2 = 2 sin t см. Найти амплитуду A результирующего колебания, его частоту ν и начальную фазу φ. Написать уравнение движения.задача 21745
Два когерентных источника звуковых волн находятся на расстояниях 3,5 м и 2,3 м от микрофона. Вычислите отношение амплитуды результирующего и исходного колебаний. Длина волны равна 0,30 м. Как изменится амплитуда результирующего колебания, если расстояние до первого источника уменьшить до 3,05 м?задача 21755
Частица одновременно участвует в двух колебаниях одного направления: x1 = 4cos4πt (см) и x2 = 3cоs(4πt + π/2) (см). Найти циклическую частоту ω, амплитуду А и начальную фазу α результирующего колебания частицы. Построить векторную диаграмму.задача 22224
Мембрана микрофона участвует в двух колебаниях: x1 = 3cos(400t), мм; x2 = 3cos(405t), мм. Записать уравнение результирующего колебания, определить амплитуду, частоту и период биений.задача 22227
Сложить 18 сонаправленных колебаний, фаза каждого последующего колебания сдвинута относительно фазы предыдущего колебания на π/3. Написать уравнение результирующего колебания, если амплитуды всех колебаний А1 = 2 см, а период колебаний равен 0,2 с.задача 22228
Частица участвует одновременно в двух гармонических колебаниях, совершающихся по взаимно перпендикулярным направлениям. Заданы частоты колебаний ν1 = 13 Гц, ν2 = 13 Гц, их амплитуды А1 = 14 см, А2 = 18 см и начальные фазы π/3 рад и π/6 рад. Напишите уравнения исходных колебании. Найдите уравнение траектории результирующего движения в координатах XOY и постройте ее график. Укажите на графике положение частицы в начальный момент времени и направление движения по траектории.задача 22446
Используя векторную диаграмму сложить 3 сонаправленных колебания: х1 = 3sin(ωt), см; х2 = 4cos(ωt), см; х3 = 5cos(ωt + 3π/4), см. Записать уравнение результирующего колебания, если ω = 2 paд/c.задача 22447
Используя векторную диаграмму сложить 3 сонаправленных колебания: х1 = 3sin(ωt), см; х2 = 4cos(ωt), см; х3 = 5cos(ωt + 3π/4), см. Записать уравнение результирующего колебания, если ω = 2 paд/c.задача 22500
В точку наблюдения приходят колебания от двух источников: y1 = 2,3cos(2,4t–5,8) и y2 = 6,8cos(2,4t+1,9). Какова будет амплитуда результирующего колебания?задача 22569
Частица участвует одновременно в двух гармонических колебаниях, совершающихся по взаимно перпендикулярным направлениям. Заданы частоты колебаний ν1 = 2 Гц, ν2 = 2 Гц, их амплитуды А1 = 3 см, А2 = 7 см и начальные фазы π/2 рад и 4π/3 рад. Напишите уравнения исходных колебаний. Найдите уравнение траектории результирующего движения в координатах ХOΥ и постройте ее график. Укажите на графике положение частицы в начальный момент времени и направление движения по траектории.задача 22570
Точка участвует в двух гармонических колебаниях одного направления: x1 = 3·cos(10πt + π/2), см; х2 = 4·cos(10πt+π/3), см. Записать уравнение результирующего колебания.задача 22571
Тело массой 120 г участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 7 Гц одинакова для обоих колебаний, начальные фазы имеют значения 2π/3 рад и -π/3 рад, а амплитуды соответственно равны 10 см и 5 см. Запишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания, запишите его уравнение. Найдите колебательную энергию тела.задача 22572
Частица участвует одновременно в двух гармонических колебаниях, совершающихся по взаимно перпендикулярным направлениям. Заданы частоты колебаний ν1 = 20 Гц, ν2 = 20 Гц, их амплитуды А1 = 10 см, А2 = 20 см и начальные фазы π/2 рад и π/4 рад. Напишите уравнения исходных колебаний. Найдите уравнение траектории результирующего движения в координатах ХОУ и постройте ее график. Укажите на графике положение частицы в начальный момент времени и направление движения по траектории.задача 22574
С помощью векторной диаграммы сложить три сонаправленных колебания с равными частотами, соотношение между амплитудами которых имеет вид: А1 : А2 : А3 = 3 : 2 : 1. Определить амплитуду результирующего колебаний, если начальные фазы исходных колебаний равны нулю, а амплитуда первого колебаний А1 = 1 см. Записать уравнение результирующего колебания и построить график зависимости от времени, если период колебаний равен 2 с.задача 22576
Складываются два сонаправленных колебания с амплитудами А1 = А2 = 1 см. Амплитуда результирующего колебания равна 1 см. Записать уравнения исходных колебаний, если начальная фаза первого колебания α1 = 0, а периоды обоих колебаний одинаковы и равны 0,1 с.задача 22577
Складываются три гармонических колебаний одного направления с одинаковыми периодами по 2 с каждый и одинаковыми амплитудами каждая по 3 см. Начальные фазы колебаний равны соответственно нулю, π/3 рад и 2π/3 рад. Запишите уравнение результирующего колебания.задача 22578
Складываются четыре сонаправленных колебания: x1 = 2cos(πt), мм, x2 = 2cos(πt + π/6), мм, x3 = 2sin(πt), мм, x4 = 2sin(πt – π/3), мм. Для сложения применить метод векторных диаграмм, записать уравнение результирующего колебания и построить график в зависимости от времени.задача 22910
Точка участвует одновременно в двух гармонических колебаниях одного направления: X1 = 3 Cos 10,4πt, см; Х2 = 3 Cos 10πt, см. Записать уравнение результирующего колебания. Определить период биения, период колебания и число колебаний точки за один период биения. Укажите значение max и min амплитуды результирующего колебания.задача 23133
Материальная точка участвует в двух колебаниях, выраженных уравнениями х1 = 3 cos t, см, х2 = 3 cos (t + π/3), см. Написать уравнение результирующего колебания.задача 23164
Точка участвует в двух взаимно перпендикулярных колебаниях x = sin πt и у = 4 sin(πt + π/2). Найти траекторию результирующего движения и начертить ее с соблюдением масштаба.задача 23452
Складываются три гармонических колебания одного направления с одинаковыми периодами Т1 = Т2 = Т3 = 2 с и амплитудами А1 = А2 = А3 = 3 см. Начальные фазы колебаний φ1 = 0, φ2 = π/3, φ3 = 2π/3. Построить векторную диаграмму сложения амплитуд. Определить амплитуду А и начальную фазу φ результирующего колебания. Записать его уравнение.задача 23456
Определить амплитуду А и начальную фазу φ0 результирующего колебания, которое возникает при сложении двух колебаний одинакового направления с одинаковыми периодами: х1 = А1sinωt, х2 = А2sinω(t+τ), где А1 = А2 = 1 см, ω = π с–1, τ = 0,5 с. Написать уравнение результирующего движения. Построить с соблюдением масштаба векторную диаграмму сложения амплитуд.задача 23466
Складываются два гармонических колебания, происходящих в одном направлении: x1 = 2cos2πt см и x2 = 3cos(2πt+π/3) см. Напишите уравнение результирующего колебания и постройте векторную диаграмму сложения амплитуд.задача 23613
Материальная точка участвует в двух колебаниях одинакового периода с начальными формами π/6 и π/3. Амплитуды колебаний 4 см и 6 см. Найти амплитуду результирующего колебания, если колебание произойдет в одном направлении.задача 23627
Складываются два колебания одинакового направления, выраженные уравнениями х1 = А1 cos ω(t + τ1) и x2 = A2 cos ω(t + τ2), где А1 = 1 см , А2 = 2 см, τ1 = 1/6 с, τ2 = 1/2 с, ω = π с–1. Определить: 1) начальные фазы φ1 и φ2 составляющих колебаний; 2) амплитуду А и начальную фазу φ0 результирующего колебания. Написать уравнение результирующего колебания. Изобразить векторную диаграмму сложения амплитуд.задача 24010
Точка участвует в двух одинаково направленных колебаниях: x1 = A1sin ωt и х2 = A2cos ωt, где А1 = 3 см, А2 = 4 см, ω = 2 с–1. Определить амплитуду А результирующего колебания, его частоту f и начальную фазу φ0. Найти уравнение этого движения.задача 24191
По данным таблицы найдите графически амплитуду и начальную фазу результирующих колебаний, возникающих при сложении двух колебаний одного направления:x1 = A1cos(ω0t + φ01) и x2 = A2cos(ω0t + φ02).
| А1, см | φ01 | А2, см | φ02 |
| 3 | 0 | 2 | –π/3 |
задача 24526
Складываются два гармонических колебания одинаковой частоты и одинакового направления: х1 = А1cos(ωt+φ1) и х2 = А2cos(ωt+φ2). Начертить векторную диаграмму для момента времени t = 0. Определить аналитически амплитуду А и начальную фазу φ результирующего колебания. Построить векторную диаграмму сложения амплитуд. Найти уравнение результирующего колебания (в тригонометрической форме через косинус). Задачу решить для случая: А1 = 1 см, φ1 = π/3, А2 = 2 см, φ2 = 5π/6.задача 24745
Складываются два гармонических колебания одинаковой частоты и одинакового направления: х1 = А1cos(ωt+φ1), x2 = A2cos(ωt+φ2). Начертить векторную диаграмму для момента времени t = 0. Определить аналитически амплитуду А и начальную фазу φ результирующего колебания. Найти уравнение результирующего колебания (в тригонометрической форме через косинус), если А1 = 1 см, φ1 = 2π/3, А2 = 1 см, φ1 = 7π/6.задача 25043
Движение точки можно представить как сложение двух колебаний одного направления и одинаковой частоты x1(t)=A1cos(ωt+α1) и x2(t)=A2cos(ωt+α2), где A1=2 см, A2=2 см, α1=0 рад, α2=π/3 рад, ω=0,4π рад/с, t=1 с.а) Постройте с соблюдением масштаба векторную диаграмму сложения колебаний;
б) Определите амплитуду A и начальную фазу α результирующего колебания, запишите его уравнение;
в) Определите смещение точки от положения равновесия и ее скорость в момент времени t.
задача 25044
Движение точки можно представить как сложение двух колебаний одного направления и одинаковой частоты x1(t)=A1cos(ωt+α1) и x2(t)=A2cos(ωt+α2), где A1=3 см, A2=2 см, α1=π/3 рад, α2=0 рад, ω=0,8π рад/с, t=0,5 с. а) Постройте с соблюдением масштаба векторную диаграмму сложения колебаний; б) Определите амплитуду A и начальную фазу α результирующего колебания, запишите его уравнение; в) Определите смещение точки от положения равновесия и ее скорость в момент времени t.задача 25045
Движение точки можно представить как сложение двух колебаний одного направления и одинаковой частоты x1(t)=A1cos(ωt+α1) и x2(t)=A2cos(ωt+α2), где A1=1 см, A2=3 см, α1=0 рад, α2=2π/3 рад, ω=π рад/с, t=1 с.а) Постройте с соблюдением масштаба векторную диаграмму сложения колебаний;
б) Определите амплитуду A и начальную фазу α результирующего колебания, запишите его уравнение;
в) Определите смещение точки от положения равновесия и ее скорость в момент времени t.
задача 25046
Движение точки можно представить как сложение двух колебаний одного направления и одинаковой частоты x1(t)=A1cos(ωt+α1) и x2(t)=A2cos(ωt+α2), где A1=2 см, A2=1 см, α1=π/2 рад, α2=π рад, ω=2π рад/с, t=0,5 с. а) Постройте с соблюдением масштаба векторную диаграмму сложения колебаний; б) Определите амплитуду A и начальную фазу α результирующего колебания, запишите его уравнение; в) Определите смещение точки от положения равновесия и ее скорость в момент времени t.задача 25047
Движение точки можно представить как сложение двух колебаний одного направления и одинаковой частоты x1(t)=A1cos(ωt+α1) и x2(t)=A2cos(ωt+α2), где A1=2 см, A2=2 см, α1=π/6 рад, α2= –π/6 рад, ω=π рад/с, t=1 с. а) Постройте с соблюдением масштаба векторную диаграмму сложения колебаний; б) Определите амплитуду A и начальную фазу α результирующего колебания, запишите его уравнение; в) Определите смещение точки от положения равновесия и ее скорость в момент времени t.задача 25151
Складываются два гармонических колебания одного направления, описываемых уравнениями х1 = 3cos2πt см и х2 = 3cos(2πt+π/4) см. Определить для результирующего колебания амплитуду и начальную фазу, записать уравнение результирующего колебания. Представить векторную диаграмму сложения амплитуд.задача 26110
Складываются два гармонических колебания одного направления, описываемых уравнениями x1 = 3cos(2πt+π/4) см и x2 = 5cos(2πt+π/2) см. Определить для результирующего колебания амплитуду, начальную фазу. Записать уравнение результирующего колебания.задача 26116
Складываются два гармонических колебания одного направления, описываемых уравнениями x1 = 3cos(πt+π/6) см и x2 = 4cos(πt+π/3), см. Определить для результирующего колебания амплитуду А, начальную фазу α. Записать уравнение результирующего колебания.задача 26118
Частица принимает участие одновременно в трех гармонических колебаниях, происходящих вдоль одного направления по законам: x1 = 6cos(ωt) см, x2 = 4cos(ωt+π/2) см, x3 = 2cos( ωt+π) см. Определить графическим методом амплитуду и начальную фазу результирующего колебания.задача 26432
В вершинах шестиугольника помещены одинаковые положительные заряды 10 нКл каждый. Какой отрицательный заряд надо поместить в центре шестиугольника, чтобы результирующая сила, действующая на каждый заряд, была равна нулю?задача 26545
а) Два одинаково направленных гармонических колебания одного периода с амплитудами 5 см и 7 см складываются в одно гармоническое колебание с амплитудой 9 см. Определить разность фаз складываемых колебаний. б) Наибольшая скорость первого колебания равна 50 см/с. Определить наибольшую скорость результирующего колебания.задача 40609
Частица принимает участие одновременно в трех гармонических колебаниях, происходящих вдоль одного направления по законам: x1 = 2cos(ωt) см, x2 = 4cos(ωt+π/4) см, x3 = 2cos(ωt+π/2) см. Определить графическим методом амплитуду и начальную фазу результирующего колебания.задача 40648
По данным уравнениям двух простых гармонических колебаний одинаковой частоты найти амплитуду и начальную фазу результирующего колебания у = у1+у2: у1 = sin (2/3 t – π/4) и у2 = sin (2/3 t + 5π/12).задача 40649
По данным уравнениям двух простых гармонических колебаний одинаковой частоты найти амплитуду и начальную фазу результирующего колебания у = у1+у2: у1 = 2sin (2t + π/3) и у2 = 3sin (2t – π/3).задача 40650
По данным уравнениям двух простых гармонических колебаний одинаковой частоты найти амплитуду и начальную фазу результирующего колебания у = у1+у2: у1 = 2sin t/2 и у2 = 2sin (t/2 + 2π/3).задача 40687
Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения двух одинаково направленных колебаний, заданных уравнениями x1 = 4sinπt см и x2 = 3sin(πr + π/2) см. Найти уравнение результирующего колебания.задача 40692
Складываются два гармонических колебания одного направления с одинаковыми периодами по 1,5 с и одинаковыми амплитудами по 2 см. Начальные фазы колебаний соответственно π/3 и π/2. Определить амплитуду и начальную фазу результирующего колебания. Записать его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд.задача 40699
Точка участвует в двух колебаниях одного направления х1 = A1Cosωt і х2 = A2Cos(ω(t+τ)), де А1 = 4 см, А2 = 3 см, ω = π рад/с, τ = 0,5 с. Выполнить рисунок и методом векторных диаграмм найти уравнение результирующих колебаний.задача 40708
Точка участвует в двух колебаниях поперечного направления х = Acosωt и y = Bsin(ω(t+τ)), где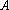 = 5 см,
= 5 см, 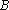 = 3 см, τ = 1 с, ω = π рад/с. Найти уравнение траектории
= 3 см, τ = 1 с, ω = π рад/с. Найти уравнение траектории 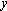 (x) результирующего колебания и построить его, указав направление движения точки вдоль траектории.
(x) результирующего колебания и построить его, указав направление движения точки вдоль траектории.
задача 60443
В вершинах квадрата со стороной 41 см находятся одинаковые одноименные заряды по 61 нКл. Какой заряд противоположного знака в нКл необходимо поместить в центре квадрата, чтобы результирующая сила, действующая на каждый заряд, была равна нулю?задача 70169
По двум большим кругам шара, вертикальному и горизонтальному, проходят токи 64 A и 69 А. На угол между направлением результирующего вектора магнитной индукции в центре шара и плоскостью вертикального витка c током.
угол между направлением результирующего вектора магнитной индукции в центре шара и плоскостью вертикального витка c током.
задачи 23.1-23.25 (С.М.Новиков: Сборник заданий по физике, 2006 г.)
По данным таблицы 1.14 найдите графически амплитуду и начальную фазу результирующих колебаний, возникающих при сложении двух колебаний одного направления:x1 = A1cos(ω0t + φ01) и x2 = A2cos(ω0t + φ02).
Таблица 1.14 (к задачам 23.1-23.25)
| Номер задачи | А1, см | φ01 | А2, см | φ02 | код | |
| 23.1 | 3 | π/4 | 2 | 2π/3 | Решение | 24186 |
| 23.2 | 2 | 5π/6 | 2 | –π/4 | Решение | 24187 |
| 23.3 | 3 | π/2 | 3 | –5π/6 | Решение | 24188 |
| 23.4 | 3 | –5π/6 | 2 | –π/4 | Решение | 24189 |
| 23.5 | 2 | π/4 | 2 | π | Решение | 24190 |
| 23.6 | 3 | 0 | 2 | –π/3 | Решение | 24191 |
| 23.7 | 2 | –π/4 | 3 | π/6 | Решение | 24192 |
| 23.8 | 3 | π | 2 | 2π/3 | Решение | 24193 |
| 23.9 | 4 | –3π/4 | 2 | –π/3 | Решение | 24194 |
| 23.10 | 2 | 3π/4 | 4 | π/3 | Решение | 24195 |
| 23.11 | 4 | –2π/3 | 2 | π/4 | Решение | 24196 |
| 23.12 | 2 | –π/4 | 4 | π/2 | Решение | 24197 |
| 23.13 | 3 | 0 | 2 | π/3 | Решение | 24198 |
| 23.14 | 2 | 2π/3 | 3 | –2π/3 | Решение | 24199 |
| 23.15 | 2 | –3π/4 | 4 | π/6 | Решение | 24200 |
| 23.16 | 3 | π/4 | 2 | –π/4 | Решение | 24201 |
| 23.17 | 2 | π | 3 | π/3 | Решение | 24202 |
| 23.18 | 2 | π/2 | 4 | 5π/6 | Решение | 24203 |
| 23.19 | 2 | –2π/3 | 2 | π/2 | Решение | 24204 |
| 23.20 | 2 | 0 | 3 | 3π/4 | Решение | 24205 |
| 23.21 | 3 | π/2 | 3 | π/3 | Решение | 24206 |
| 23.22 | 2 | 2π/3 | 2 | –π/6 | Решение | 24207 |
| 23.23 | 2 | –π/3 | 3 | π/3 | Решение | 24208 |
| 23.24 | 4 | 5π/6 | 2 | π/6 | Решение | 24209 |
| 23.25 | 3 | 0 | 2 | –5π/6 | Решение | 24210 |