Заказать решения
Задачи по физике (рус)
Задачі з фізики (укр)
Вопросы по физике:
6 класс Другие предметы
Витамины для ума Лучшая книга о разуме
|
заряжен бесконечная протяженная плоскость заряд расстояние поле находит
задача 13024
На расстоянии 40 см or заряженной бесконечно протяженной плоскости с поверхностной плотностью заряда 77 нКл/м2 находится одноимённо заряженный бесконечно длинный проводящий цилиндр диаметром 620 мкм с поверхностной плотностью заряда 47 мКл/м2. Определить разность потенциалов между цилиндром и плоскостью.
задача 14104
На расстоянии 8 см от бесконечно протяженной заряженной с поверхностной плотностью –σ = 2·10–6 Кл/м2 плоскости проведена параллельно ей бесконечно длинная нить, заряженная с линейной плотностью +τ = 8·10–7 Кл/м. Вычислить напряженность электрического поля в точке, равноотстоящей от плоскости и от нити.
задача 14589
Около заряженной бесконечно протяженной плоскости находится точечный заряд q = 0,66 нКл, имеющий массу m = 0,1 мг. Заряд перемещается по линии напряженности поля на расстояние Δr = 2 см; при этом совершается работа A = 5·10–6 Дж. Чему равна скорость заряда в конечной точке, если в начальном положении ее скорость была равна нулю?
задача 15105
С какой силой Fs на единицу площади отталкиваются две одноименно заряженные бесконечные плоскости? Поверхностная плотность заряда на плоскостях σ = 0,3 мКл/м2.
задача 15433
Вдоль силовой линии электрического поля отрицательно заряженной протяженной плоскости движется электрон. Найдите минимальное расстояние, на которое он может приблизиться к плоскости, если на расстоянии 5 см от плоскости кинетическая энергия электрона 8 кДж, а поверхностная плотность заряда плоскости 35,4 Кл/м2.
задача 15912
Плоская бесконечно протяженная пластина толщиной d = 4 см несет равномерно распределенный по объему заряд (ρ = 8 нКл/м3). В пластине имеется сферическая полость радиуса R = d/2. Определить по модулю и направлению, напряженность ЕA электрического поля в точке А, лежащей на прямой, проходящей через центр сферы перпендикулярно плоскости поверхности пластины.
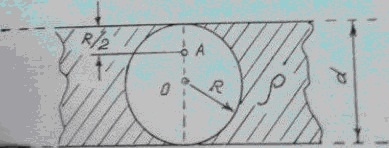
задача 15913
Плоская, бесконечно протяженная пластина, толщиной d = 4 см, несет равномерно распределенный по объему заряд (ρ = 8 нКл/м3). В пластине имеется цилиндрическая полость радиуса R = d/2. Определить по модулю и направлению, напряженность ЕA электрического поля в точке А, лежащей на прямой, перпендикулярной оси цилиндра и плоскости поверхности пластины.
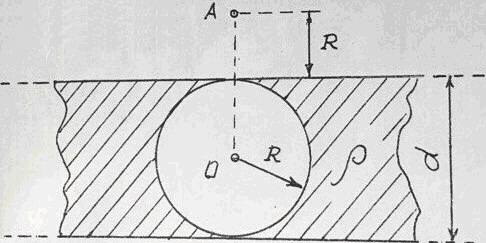
задача 17087
Бесконечно протяженная заряженная с линейной плотностью τ = 10–7 Кл/м нить образует петлю радиуса R = 0,2 м. Определить напряженность электрического поля в центре петли.
задача 17342
Методом интегрирования доказать, что напряженность электрического поля, созданного бесконечно протяженной равномерно заряженной по поверхности пластиной, в любой точке, вычисляется по формуле Е = σ/2ε0.
задача 17343
Методом интегрирования определить напряженность электрического поля, созданного бесконечно протяженной заряженной по поверхности плоскостью в точке А, отстоящей от поверхности на расстоянии S = 0,1 м. (σ = 10–9 Кл/м2).
задача 17347
Две бесконечно протяженные равномерно заряженные с поверхностной плотностью +σ1 = +σ2 = 10–7 Кл/м2 плоскости пересекаются под углом 60 градусов. Найти величину и направление напряженности электрического поля в произвольной точке, лежащей на биссектрисе двугранного угла.
задача 17351
За пределами двух бесконечно протяженных параллельных равномерно заряженных с поверхностными плотностями +σ1 = 3·10–7 Кл/м2 и –σ2 = 2·10–7 Кл/м2 пластин находится заряд +Q = 4·10–7 Кл. Чему равна сила, действующая на заряд Q?
задача 17355
Две бесконечно протяженные взаимно перпендикулярные плоскости заряжены с поверхностными плотностями σ1 = –4·10–6 Кл/м2 и σ2 = +5·10–6 Кл/м2. Найти напряженность электрического поля в точке, равноотстоящей от обеих пластин.
задача 17359
Найти поверхностную плотность заряда бесконечно протяженной плоскости, если точечный заряд Q = 10–7 Кл под действием электрического поля перемещается вдоль силовой линий на расстояние S = 2 см, при этом силы поля совершают работу равную А = 5·10–6 Дж.
задача 17366
Дана бесконечно протяженная равномерно заряженная объемной плотностью ρ = 10–5 Кл/м3 пластина толщиной d = 2 см. Найти разность потенциалов между двумя точками, лежащими вдоль одной прямой на расстояниях а = 4 см и b = 5 см от центра пластины.
задача 17368
Электрическое поле образовано бесконечно протяженной равномерно заряженной с поверхностной плотностью заряда σ = 40·10–9 Кл/м2 плоскостью. Определить разность потенциалов в двух точках, лежащих на перпендикуляре к плоскости и отстоящих от плоскости на расстояниях А = 15 см и В = 20 см.
задача 17421
Около заряженной бесконечно протяженной плоскости находится точечный заряд q = 70 нКл. Под действием поля заряд перемещается по силовой линии на расстояние Δr = 2 см, при этом силы поля совершают работу А = 5 мкДж. Найти поверхностную плотность заряда на плоскости.
задача 20947
Около заряженной бесконечно протяженной плоскости находится точечный заряд q = 0,66 нКл. Заряд перемещается по линии напряженности поля на расстояние l = 2,0 см. При этом совершается работа A = 5,0·10–7 Дж. Найдите поверхностную плотность заряда σ на плоскости.
задача 21197
Параллельно протяженной плоскости расположена длинная нить. С какой силой будет действовать электрическое поле плоскости на каждый метр длины нити, если плоскость заряжена с поверхностной плотностью заряда σ, а нить — с линейной плотностью заряда τ?
задача 22832
Используя теорему Гаусса, найдите напряженность поля, создаваемого бесконечно протяженной заряженной нитью, как функцию расстояния r от нити. Линейная плотность заряда нити равна τ = 5,0 нКл/м. Постройте график зависимости Е = f(r).
задача 22833
Используя теорему Гаусса, найдите напряженность поля, создаваемого тонкостенным, бесконечно протяженным, металлическим цилиндром радиуса R = 5,0 см, как функцию расстояния r от оси цилиндра. Поверхностная плотность заряда цилиндра равна σ = 10 нКл/м2. Постройте график зависимости Е = f(r).
задача 24505
Используя теорему Гаусса, найдите напряженность поля, создаваемого стеклянной бесконечно протяженной пластиной толщиной h = 10 см, как функцию расстояния r от центра пластины. Объемная плотность заряда пластины равна ρ = 20 нКл/м3. Постройте график зависимости Е = f(r). Диэлектрическая проницаемость стекла ε = 6.
задача 24712
Используя теорему Гаусса, найдите напряженность поля, создаваемого сплошным стеклянным, бесконечно протяженным цилиндром радиуса R = 1,0 см, как функцию расстояния r от оси цилиндра. Объемная плотность заряда цилиндра равна ρ = 20 нКл/м3. Постройте график зависимости Е = f(r). Диэлектрическая проницаемость стекла ε = 6.
задача 24717
Поток вектора напряжённости ФЕ, создаваемого бесконечно протяженной заряженной нитью, через боковую поверхность S цилиндра равен 1) ФЕ = 0; 2) ФЕ = E·S·cos90°; 3) ФЕ = E·S·cos0°; 4) ФЕ = E·S·cos180°.
задача 24718
Поток вектора напряжённости ФЕ, создаваемого бесконечно протяженной заряженной нитью, через верхнее основание цилиндра площадью S, равен 1) ФЕ = 0, 2) ФЕ = E·S·cos90°, 3) ФЕ = E·S·cos0°, 4) ФЕ = E·cos0°.
задача 60408
На расстоянии 20 см от заряженной бесконечно протяженной плоскости c поверхностной плотностью заряда 25 нKл/м2 находится одноименно заряженный бесконечно длинный проводящий цилиндр диаметром 24,8 мкм c поверхностной плотностью заряда 33 мKл/м2. Определить разность потенциалов между цилиндром и плоскостью.
задача 60611
Поле создается сплошным стеклянным бесконечно протяженным цилиндром радиуса R = 15 см. Объемная плотность его равна 20 нКл/м3. Определить напряженность поля как функцию расстояния от центра цилиндра, используя теорему Гаусса. Построить график зависимости E = f(r). ε = 7.
|