точка двигается по траектории со скоростью направление уравнение движения найти время где
задача 10072
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых х=A1sinω1t и у=А2cosω2t, где A1=8 см, A2=4 см, ω1=ω2=2 с–1. Написать уравнение траектории и построить ее. Показать направление движения точки.задача 10573
Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих согласно уравнениям: x = A1cos ω1t; y = A2sin ω2t, где A1 = 3 см; ω1 = l с , A2 = 2 см; ω2 = 1 с–1. Определить траекторию точки. Построить траекторию с соблюдением масштаба, указать направление движения точки.задача 10573
Двое происходящих одновременно взаимно перпендикулярных колебаний материальной точки описываются уравнениями: x = А1cos ω1t; y = A2sin ω2t, где А1 = 3 см; ω1 = l с , A2 = 2 см; ω2 = 1 с–1. Найдите траекторию точки. Постройте траекторию с учетом масштаба, укажите направление движения точки.задача 10576
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых: x = A1 sin ω1t и y = А2 cos ω2t, где А1 = 2 см; A2 = 1 см; ω1 = ω2 = 1 с–1. Написать уравнение траектории и построить ee на чертеже; показать направление движения точки.задача 10578
Точка участвует в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: х = A1cos ω1t и у = A2cos ω2t, где A1 = 2 см; A2 = 3 см; ω1 = 2ω2. Найти уравнение траектории точки и построить ее на чертеже; показать направление движения точки.задача 11014
Движение точки по кривой задано уравнениями x = A1t3 и y = A2t, где A1 = 1 м/с3, A2 = 2 м/с. Найти уравнение траектории точки, ее скорость v и полное ускорение а в момент времени t = 0,8 с.задача 11323
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями x = A1cosωt и y = A2sinωt, где A1 = 2 см, A2 = 1 см. Найти уравнение траектории точки и построить ее, указав направление движения.задача 11377
Точка совершает одновременно два колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = 8cosπt, y = 8cosπ(t+1) (длина в сантиметрах, время в секундах). Найти уравнение траектории и построить график её движения.задача 11396
По прямой линии движутся две материальные точки согласно уравнениям: х1 = 10 + t + 2t2 и x2 = 3 + 2t + 0,2t2. В какой момент времени скорости этих точек одинаковы?задача 12241
Тело движется согласно уравнению x = 7 + 4t, y = 2 + 3t. Какова скорость движения точки?задача 12594
Определить неточность Δх в определении координаты электрона, движущегося в атоме водорода со скоростью v = 1,5·106 м/с, если допускаемая неточность Δv в определении скорости составляет 10 % от ее величины. Сравнить полученную неточность с диаметром d атома водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.задача 12655
Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых в единицах СИ имеют вид x = 0,4 cos πt и у = 0,2 cos π(t–0,5). Определить траекторию движения точки и начертить её с соблюдением масштаба. Рассчитать и указать на чертеже скорость и ускорение точки в начальный момент времени и указать направление её движения по кривой. Если траектория не замкнутая, то указать пределы движения.задача 12956
Точка движется по прямой согласно уравнению x = At – Bt3 – С, где А = 4 м/с, В = 3 м/с3, С = 1 м. Найти координаты х точки в моменты времени, когда скорость v равна нулю.задача 13010
С башни высотой h = 30 м в горизонтальном направлении брошено тело с начальной скоростью v0 = 10 м/с. Определите: 1) уравнение траектории тела у(х); 2) скорость и тела в момент падения на Землю; 3) угол φ, который образует эта скорость с горизонтом в точке его падения.задача 13010
Тело бросили с башни высотой h = 30 м с начальной скоростью v0 = 10 м/с в горизонтальном направлении. Найти: 1) уравнение траектории тела у(х); 2) скорость u тела в момент приземления; 3) угол φ, образованный вектором скорости с горизонтом в точке падения.задача 13021
Точка движется в плоскости xу из положения с координатами х1 = у1 = 0 со скоростью v = аi + bхj (a, b - постоянные, i, j - орты осей х и у). Определите: 1) уравнение траектории точки у(x); 2) форму траектории.задача 13099
Тело брошено под углом α = 45° к горизонту со скоростью v0 = 15 м/с Используя закон сохранения энергии, определите скорость v тела в высшей точке его траектории.задача 13099
Начальная скорость тела v0 = 15 м/с направлена под углом α = 45° к горизонту. С помощью закона сохранения энергии найти скорость v тела в наивысшей точке траектории.задача 14427
С башни высотой h = 25 м горизонтально брошен камень со скоростью vx = 15 м/с. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью v он упадет на землю? Какой угол φ составит траектория камня с горизонтом в точке его падения на землю?задача 14428
Камень, брошенный горизонтально, упал на землю через время t = 0,5 с на расстоянии l = 5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью vx он брошен? С какой скоростью он упадет на землю? Какой угол φ составит траектория камня с горизонтом в точке его падения на землю?задача 14440
С башни высотой h0 = 25 м бросили камень со скоростью v0 = 15 м/с под углом α = 30° к горизонту. Какое время t камень был в полете? На каком расстоянии l от основания башни он упал на землю? С какой скоростью v он упал на землю? Какой угол φ составила траектория камня с горизонтом в точке его падения на землю?задача 14517
Камень бросили со скоростью v0 = 15 м/с под углом α = 60° к горизонту. Найдите кинетическую Wк, потенциальную Wп и полную W энергии камня: а) через одну секунду после начала движения; б) в наивысшей точке траектории. Масса камня m = 0,2 кг.задача 14854
Два электрона движутся в однородном магнитном поле по круговым траекториям R1 > R2. Сравнить их угловые скорости.задача 14857
Однозарядные ионы О+ изадача 15304
Точка движется в плоскости так, что ее движение описывается уравнениями x = 3t; y = 3t(1+0,5t). Найти путь, пройденный материальной точкой за 2 секунды; модуль скорости в этот момент времени. Записать уравнение траектории движения материальной точки; уравнения радиус вектора; вектора скорости и вектора ускорения.задача 15531
4 октября 1957 г. в СССР произведен запуск первого в мире искусственного спутника Земли. Спутник имел форму шара диаметром 58 см, масса его 83,6 кг; спутник описывал эллиптические траектории вокруг Земли, причем в некоторые моменты достигал высоты 900 км над поверхностью Земли. Период обращения спутника вокруг Земли оказался равным 1 часу 36,2 мин. Предположим, что спутник двигался вокруг центра Земли по круговой траектории. Какой высоте над поверхностью Земли, какой скорости и какой кинетической энергии соответствовал бы в таком случае указанный период обращения?задача 16055
Камень брошен горизонтально со скоростью 15 м/с. Найти уравнение траектории камня и его полную скорость через время t = 2 с после броска.задача 16081
Точка движется так, что вектор ее скорости V меняется со временем по закону V = 2i + 2tj + 2t2k (м/с). Найти модуль перемещения |Δr| за первые 4 с её движения; модуль скорости в момент времени t = 4 c.задача 16449
Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях х = 2 cos t/2, у = –cos t. Определить уравнение траектории и начертить ее с соблюдением масштаба.задача 16566
Точка участвует в двух взаимно-перпендикулярных колебаниях: х = А1 cos ω1t и у = А1 cos ω2t. Отношение частот складываемых колебаний 1:2. Найти уравнение траектории точки, построить график и указать направление движения.задача 17200
Движение точки задано уравнениями x = A1sinωt и y = A2sinω(t+τ), где А1 = 10 см, А2 = 5 см, ω = 2 рад/с, τ = π/4 с. Найти уравнение траектории и скорости точки в момент времени t = 0,5 с.задача 17203
Движение материальной точки задано уравнением x = At + 2Bt2, где А = 0,8 м/с, В = –0,1 м/с2. Вычислить среднее значение модуля скорости <v> за первые 4 с движения.задача 17496
Материальная точка двигается так, что ее координаты изменяются в зависимости от времени согласно уравнениям x = A·sin(ω·t); y = A·sin(2ω·t). Запишите уравнение траектории, постройте график у = f(x), определите скорость точки через t1 = 1 с, если А = 1 см, ω = π рад/c.задача 17510
Зависимости координат материальной точки по двум взаимно перпендикулярным направлениям описывается уравнениями: x(t) = 3sin 3t, y(t) = 6cos 3t, см. Вычислите: 1) зависимость скорости и ускорения от времени; 2) модули скорости и ускорения в момент времени t = 0,2 с; 3) максимальную скорость точки; 4) уравнение траектории движения точки у = f(x); 5) постройте график зависимости у = f(х) и определите координаты точек траектории, в которых скорость точки наибольшая и наименьшая. Изобразите их на графике; 6) назовите характер движения точки.задача 17745
Точка движется в плоскости х0у по закону: x = 2sinωt; у = 2cosωt. Найти путь, пройденный телом за 2 с; угол между векторами скорости v и ускорения a; траекторию движения y = f(x).задача 17805
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых имеют вид: Х = 2 Sin ωt, см; Y = Cos 2ωt, см. Найти уравнение траектории движения точки и построить траекторию на чертеже, соблюдая масштаб. Определить начальное положение точки и указать направление движения (вектор скорости) в этот момент времени.задача 17961
Складываются два взаимно перпендикулярных колебания:х = 2·cos(ω·t), см;
у = 4·sin(ω·t), см.
Определить уравнение траектории y = f(x), построить график.
задача 18113
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями х = A1 cos(ωt), y = A2 sin(0,5ωt), где A1 = 2 см, A2 = 3 см. Найти уравнение траектории точки и построить ее, указав направление движения.задача 18114
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями х = A1 cos(ωt), y = A2 sin(0,5ωt), где A1 = 2 см, A2 = 4 см. Найти уравнение траектории точки и построить ее, указав направление движения.задача 19691
Точка движется в плоскости XY вдоль оси X равномерно со скоростью Vx = 0,5 м/с, а вдоль оси Y так, что уравнение траектории имеет вид y = 0,2x2 + 15x3. Найти зависимость скорости движения точки вдоль оси Y от времени, полагая, что при t = 0 точка находилась в начале координат.задача 19947
Точка участвует в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями х = 2 sinωt и у = 3 cosωt. Записать уравнение траектории точки и нарисовать ее траекторию, показав направление движения точки по траектории.задача 19948
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями x = 3cosωt и y = –6cosωt. Получить уравнение траектории точки, нарисовать ее и показать направление движения точки.задача 20081
Материальная точка участвует одновременно в двух колебаниях, происходящих вдоль взаимно перпендикулярных осей, по законам: x = 0,1sin(2t+π); y = 0,2sin(2t+π), где x и y — соответствующие координаты точки; t — время в секундах. Найти уравнение траектории результирующего движения, величину и направление вектора скорости в начальный момент времени. Построить траекторию движения (в масштабе).задача 20135
Материальная точка имеет массу m = 9 кг и движется по криволинейной траектории под действием силы, проекция которой на касательную Fτ = 5,7 Н, на нормаль Fn = 2·t2 Н. Определите модуль ускорения точки в момент времени t = 19,8 с.задача 20186
Уравнение движения материальной точки задается в параметрической форме: x = 4cos3πt, y = 4sin3πt. Построить траекторию движения материальной точки и найти путь и перемещение за время от t1 = 1 с до t2 = 4 с.задача 20188
Уравнение движения материальной точки задается в параметрической форме: x = 4cos3πt, y = 4sin3πt. Построить траекторию движения материальной точки и найти путь и перемещение за время от t1 = 2 с до t2 = 4 с.задача 20189
Уравнение движения материальной точки задается в параметрической форме: x = 2cos2πt, y = 2sin2πt. Построить траекторию движения материальной точки и найти путь и перемещение за время от t1 = 0,5 с до t2 = 3 с.задача 20387
От удара футбольный мяч получает скорость 20 м/с под углом 45° к горизонту. Определить его скорость в верхней точке траектории, максимальную высоту подъёма, время движения и на каком расстоянии он упадет на Землю?задача 20820
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: x = 2sinπt см и y = –cosπt см. Запишите уравнение траектории результирующего движения точки и постройте ее, указав направление движения.задача 20825
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: x = 2cosπt см и y = 4sinπt см. Запишите уравнение траектории результирующего движения точки и постройте ее, указав направление движения.задача 21392
Точка движется по прямой согласно уравнению х(t) = A cos(ωt). Найти зависимость силы, действующей на точку, от ее координаты х. Масса точки m. А и ω — постоянные.задача 21404
Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями x = 2sin πt см и у = sin π(t + 0,5) см. Найти уравнение траектории, построить график, показав направление движения точки.задача 21413
Точка движется по прямой согласно уравнению x(t) = 4sin(ωt). Найти зависимость силы, действующей на точку, от ее координаты х. Масса точки m. А и ω — постоянные.задача 21909
Точка движется в плоскости ху по закону x = αt, у = αt(1–βt), где α и β — положительные постоянные. Найти: а) уравнение траектории точки у(х); изобразить ее график; б) скорость v и ускорение а точки в зависимости от t; в) момент t0, когда угол между скоростью и ускорением равен π/4.задача 22573
Частица участвует одновременно в двух взаимно перпендикулярных колебаниях, описываемых уравнениями: х = 2·cos(ωt), см; у = 3·sin(2ωt), см. Запишите уравнение и постройте график траектории частицы, укажите направление движения частицы по ней.задача 22579
Частица участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями х = 4cos(πt), см, у = 8cos(πt + π/2), см. Запишите уравнение траектории движения частицы, постройте график, укажите направление движения частицы по траектории.задача 22580
Частица участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = 4cos(πt), см, у = 4cos(πt/2 + π/2), см. Запишите уравнение траектории движения частицы, постройте график, укажите направление движения частицы по траектории.задача 22687
Материальная точка М движется по окружности со скоростью V. На рис. 1 показан график зависимости Vτ от времени (τ — единичный вектор положительного направления, Vτ — проекция V на это направление). На рис. 2 укажите направление силы, действующей на точку М в момент времени t. Ответ обоснуйте.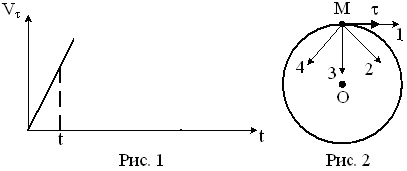
задача 22688
Материальная точка М движется по окружности со скоростью V. На рис. 1 показан график зависимости Vτ от времени (τ — единичный вектор положительного направления, Vτ — проекция V на это направление). На рис. 2 укажите направление силы, действующей на точку М в момент времени t. Ответ обоснуйте.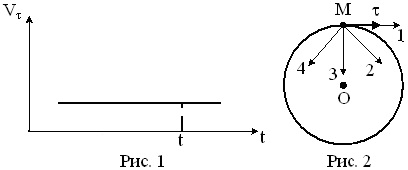
задача 22689
Материальная точка М движется по окружности со скоростью V. На рис. 1 показан график зависимости Vτ от времени (τ — единичный вектор положительного направления, Vτ — проекция V на это направление). На рис. 2 укажите направление силы, действующей на точку М в момент времени t. Ответ обоснуйте.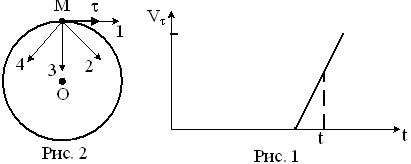
задача 22844
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями х = А1 sin ωt и у = А2 cos ωt, где А1 = 2 см, А2 = 1 см. Определить уравнение траектории точки, построить траекторию с соблюдением масштаба. Указать направление движения точки и пояснить свой ответ.задача 22879
Первая точка движется по траектории y = 5x2. Закон движения второй точки: x = 2t (м), y = 8t (м). В какой момент времени они встретятся и каковы координаты их места встречи?задача 22881
Тело движется с постоянной по величине скоростью по траектории, изображенной на рисунке. Для величин полного ускорения тела в точках А и В справедливо следующее соотношение … 1) аА < аВ 2) аА > аВ 3) аА = аВ.
задача 23157
Точка движется в плоскости хоу по закону: х = –2t; y = 4t(1–t). Найти уравнение траектории у = f(x) и изобразить ее графически; вектор скорости V и ускорения а в зависимости от времени; момент времени t0, в который вектор ускорения a составляет угол π/4 с вектором скорости V.задача 23224
Движение материальной точки в плоскости задано уравнениями х = A1sin ωt, у = A1sin(ωt+π), где A1 = 2·10–2 м, A2 = 4·10–2 м. Построить уравнение траектории и начертить график.задача 23265
Даны параметрические уравнения движения материальной точки: х = 3R·sin(ωt); у = R·cos(ωt). Определить траекторию движения точки и ее ускорение, если R = 10 м, ω = π рад/c.задача 23450
Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выраженных уравнениями х = 1 sinωt см и у = –2 cosωt см. Найдите уравнение траектории этой точки и изобразите её. Определите направление движения этой точки.задача 23453
Материальная точка участвует в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями х = А1 cos ωt и y = А2 cos 2ωt, где А1 = 2 см, А2 = 1 см. Найти уравнение траектории и построить ее.задача 23477
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, описываемых уравнениями х = А1cos ωt и у = –А2cos ωt, где А1 = 2 см, А2 = 1 см. Записать уравнение траектории точки и построить ее, указав направление движения.задача 23971
Тело движется по траектории y = 5x2 – 63x + 5, а его координата х меняется по закону x = 5t2 (x и y в м, t в с). Найти момент времени, когда направление его скорости составляет 45 градусов с осью х.задача 24099
Материальная точка участвует в двух взаимно перпендикулярныx колебанияx, выражаемыx уравнениями x = 3cos(πt), м; y = 2cos[π(t+0,5)], м. Определить траекторию точки и начертить ее в масштабе. Указать направление движения точки.задача 24146
Камень брошен под углом α = 30° к горизонту со скоростью v0 = 10 м/с (см. рис.). Требуется: 1) написать кинематические уравнения движения камня; 2) вывести уравнение траектории камня; 3) определить время τ, через которое камень окажется на высоте h = 1 м; 4) определить скорость v камня (по модулю и направлению) на высоте h = 1 м. Камень рассматривать как материальную точку и принять g = 10 м/с2.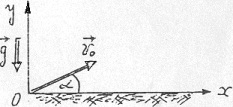
задача 24147
Тело брошено под углом α = 30° к горизонту со скоростью v0 = 20 м/с с высоты Н = 10 м. Требуется: 1) написать кинематические уравнения движения; 2) вывести уравнение траектории; 3) найти время полета τ до высоты h = 5 м; 4) определить по модулю и направлению скорость v тела на высоте h. Тело рассматривать как материальную точку и принять g = 10 м/с2.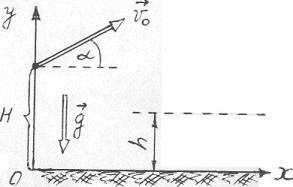
задача 24168
Частица движется в центральном поле сил с центром в точке О (см. рис.). На рисунке показан участок траектории. Считая известными v1, α, r1, β и r2, найдите v2.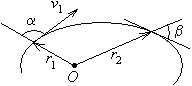
задача 24180
Траектория самолета, отображаемая на экране радара, представляет кривую, которую можно описать соотношениями x = 1000 + 200·t, y = 2000 – 100·t, z = 5000 + 2·t2 (x, y, z измеряются в метрах, t – в секундах). Найти скорость и ускорение самолета через 2 сек и через 3 сек после начала наблюдения.задача 24539
Пропеллер самолета радиусом R = 1,5 м вращается с частотой n = 2,1·103 мин–1, посадочная скорость самолета относительно Земли равна v = 161 км/ч. Какова скорость точки на конце пропеллера? Какова траектория движения этой точки?задача 24746
Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями х = А1sinωt и у = А2cosω(t+τ), где А1 = 2 см, А2 = 1 см, ω = π с–1, τ = 0,5 с. Найти уравнение траектории и построить ее, показав направление движения точки.задача 25048
Точка движется по плоскости так, что ее координаты зависят от времени в соответствии с уравнениями x(t)=Acos(ω1t+α1) и y(t)=Bcos(ω2t+α2), где A=3 см, B=2 см, α1=0 рад, α2=π/2 рад, ω1=2π рад/с, ω2=2π рад/с, t=0,25 с.а) Получите уравнение траектории точки и постройте ее с соблюдением масштаба; б) Определите координаты точки, ее скорость и ускорение в момент времени t; в) Укажите на рисунке положение точки, направления ее скорости и ускорения в начальный момент времени и в момент времени t.
задача 25049
Точка движется по плоскости так, что ее координаты зависят от времени в соответствии с уравнениями x(t)=Acos(ω1t+α1) и y(t)=Bcos(ω2t+α2), где A=2 см, B=2 см, α1=0 рад, α2= –π/2 рад, ω1= 2π рад/с, ω2= 2π рад/с, t=0,25 с.а) Получите уравнение траектории точки и постройте ее с соблюдением масштаба; б) Определите координаты точки, ее скорость и ускорение в момент времени t; в) Укажите на рисунке положение точки, направления ее скорости и ускорения в начальный момент времени и в момент времени t.
задача 25050
Точка движется по плоскости так, что ее координаты зависят от времени в соответствии с уравнениями x(t)=Acos(ω1t+α1) и y(t)=Bcos(ω2t+α2), где A=1 см, B=2 см, α1=0 рад, α2= 0 рад, ω1=π рад/с, ω2=π рад/с, t=0,5 с.а) Получите уравнение траектории точки и постройте ее с соблюдением масштаба; б) Определите координаты точки, ее скорость и ускорение в момент времени t; в) Укажите на рисунке положение точки, направления ее скорости и ускорения в начальный момент времени и в момент времени t.
задача 26241
По прямому шоссе со скоростью v1 = 16 м/с движется автобус. На расстоянии d = 60 м от шоссе и s = 400 м от автобуса находится человек. Человек может бежать со скоростью v2 = 4 м/с. В каком направлении он должен бежать, чтобы успеть "перехватить" автобус? При какой наименьшей скорости человека v2min это вообще возможно? В каком направлении необходимо при этом бежать?задача 26524
Обезьяна раскачивалась на длинной тонкой лиане так, что максимальный угол отклонения лианы от вертикали составил α. Когда обезьяна находилась в нижней точке траектории, лиана зацепилась серединой за ветку дерева. Каким стал максимальный угол β отклонения лианы от вертикали, если α < 60°? Что изменится, если 60°< α <90°?задача 26642
Точка движется по траектории согласно уравнению s = 0,5t2 + 4t. Определить, в какой момент времени скорость точки достигнет 10 м/с.задача 40132
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях: х = 2cos(πt/4) и у = 2sin (πt/4). Найти траекторию движения точки, построить ee c соблюдением масштаба.задача 40479
Материальная точка движется под действием силы согласно уравнению Х = A + Вt + Сt2 + Dt3 , где С = 1 м/c2; D = –0,2 м/c3. Определить, в какой момент времени сила равна нулю.задача 40549
Частица движется в плоскости xу из точки с координатами x = y = 0 со скоростью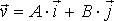
, где А и В — положительные постоянные, 
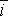и 
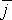— орты осей х и у. Найти уравнение траектории частицы.
задача 40563
Тело брошено со скоростью v0 под углом α к горизонту. В начальный момент времени t = 0 тело находилось в точке с координатами х = у = 0. Найти уравнение траектории движения тела.задача 40588
Частица движется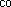
гласно уравнению r(t) = А(і cosωt + j sіnωt), где A = 0,5 м, ω = 5 с–1. Изобразите на рисунке траекторию движения. Определите моду
скорости |v| и модуль нормаль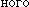
ускорения |аn|.
задача 40605
Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых имеют вид х = sin(t/2), y = сost. Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.задача 40605
Материальная точка колеблется одновременно в двух взаимно перпендикулярных направлениях. Уравнения этих колебаний имеют вид х = sin(t/2), y = сost. Определить уравнение траектории точки. Изобразить на чертеже траекторию с соблюдением масштаба, показать направление движения точки.задача 40617
Ракета пущена под углом 73 градусов к горизонту с начальной скоростью 25 м/с. Определить время горения запала ракеты, если известно, что она вспыхнула в наивысшей точке своей траектории.задача 40617
Ракета выпущена под углом 73° к горизонту с начальной скоростью 25 м/с и вспыхнула в наивысшей точке своей траектории. Найти время горения запала ракеты.задача 40664
Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых x = 3cos t, y = 2sin t. Найти траекторию точки, построить ее и указать направление движения точки.задача 40666
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях х = sinπt, y = 4sin(πt + π). Найти траекторию движения точки,
строить ее с соблюдением масштаба.
задача 40689
Материальная точка движется в соответствии с уравнением S = 5t + 2t2. Найти скорость материальной точки через две секунды после начала движения.задача 40768
Точка одновременно участвует в двух взаимно перпендикулярных колебаниях, уравнение которых имеет вид x = A1cos(ω1t) и y = A2cos(ω2t), где А1 = 100 мм, А2 = 50,0 мм, ω1 = ω2 = 2,00 с–1. Написать уравнение траектории движения точки и построить ее с соблюдением масштаба. Показать направление движения точки.задача 40883
Модель ракеты взлетает вертикально вверх с ускорением а = 4 м/с2. Двигатель модели работает в течении 10 с. Вычислите среднюю скорость за время от старта до достижения наивысшей точки траектории.задачи 24.1-24.25 (С.М.Новиков: Сборник заданий по физике, 2006 г.)
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка. Уравнения колебаний приведены в таблице 1.15.Таблица 1.14 (к задачам 24.1-24.25)
| Номер задачи | Уравнения колебаний x(t), y(t) | код | |
| 24.1 | x = A sin ωt, y = A cos 2ωt | Решение | 24211 |
| 24.2 | x = A sin 2ωt, y = A sin 3ωt | Решение | 24212 |
| 24.3 | x = A cos 3ωt, y = A cos 2ωt | Решение | 24213 |
| 24.4 | x = 2A cos ωt, y = A sin 2ωt | Решение | 24214 |
| 24.5 | x = 2A cos 3ωt, y = A sin 2ωt | Решение | 24215 |
| 24.6 | x = A sin 3ωt, y = A sin ωt | Решение | 24216 |
| 24.7 | x = 2A sin ωt, y = A sin 2ωt | Решение | 24217 |
| 24.8 | x = 2A cos 2ωt, y = A sin 3ωt | Решение | 24218 |
| 24.9 | x = A cos ωt, y = A cos 3ωt | Решение | 24219 |
| 24.10 | x = 2A sin 3ωt, y = A cos ωt | Решение | 24220 |
| 24.11 | x = A cos 3ωt, y = A sin ωt | Решение | 24221 |
| 24.12 | x = 2A cos 2ωt, y = A cos 3ωt | Решение | 24222 |
| 24.13 | x = 2A cos 2ωt, y = A sin 2ωt | Решение | 24223 |
| 24.14 | x = 2A sin ωt, y = A cos 3ωt | Решение | 24224 |
| 24.15 | x = A sin 2ωt, y = A cos 3ωt | Решение | 24225 |
| 24.16 | x = 2A cos 2ωt, y = A sin ωt | Решение | 24226 |
| 24.17 | x = A cos ωt, y = A sin 3ωt | Решение | 24227 |
| 24.18 | x = 2A sin 3ωt, y = A sin 2ωt | Решение | 24228 |
| 24.19 | x = A sin 2ωt, y = A cos ωt | Решение | 24229 |
| 24.20 | x = 2A sin ωt, y = A sin 3ωt | Решение | 24230 |
| 24.21 | x = A cos 2ωt, y = A cos ωt | Решение | 24231 |
| 24.22 | x = 2A cos 3ωt, y = A cos ωt | Решение | 24232 |
| 24.23 | x = A sin 2ωt, y = A sin ωt | Решение | 24233 |
| 24.24 | x = 2A cos ωt, y = A cos 2ωt | Решение | 24234 |
| 24.25 | x = 3A sin 3ωt, y = A cos 3ωt | Решение | 24235 |