Заказать решения
Задачи по физике (рус)
Задачі з фізики (укр)
Вопросы по физике:
6 класс Другие предметы
|
вероятный потенциальный электрон определить функция
задача 10455
Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид ψ(r) = Ae–r/a0, где А — некоторая постоянная; а0 — первый боровский радиус. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.
задача 10455
Движение электрона в атоме водорода в основном состоянии описывает волновая функция ψ(r) = Ae–r/a0, где a0 — первый боровский радиус, A — некоторая постоянная. Для основного состояния атома водорода определить наиболее вероятное расстояние от электрона до ядра.
задача 10916
Частица в потенциальном ящике шириной l находится в возбужденном состоянии (n = 2). Определить, в каких точках интервала (0<x<l) плотность вероятности нахождения частицы имеет максимальное и минимальное значения.
задача 10916
Состояние частицы в потенциальном ящике шириной l возбужденное (n = 2). Для плотности вероятности нахождения частицы в интервале (0<x<l) требуется выяснить, в каких точках интервала имеет максимальное и в каких минимальное значения.
задача 10917
Электрон находится в потенциальном ящике шириной l. В каких точках в интервале (0<x<l) плотность вероятности нахождения электрона на первом и втором энергетическом уровне одинакова? Вычислить значение плотности вероятности для этих точек. Решение пояснить графиком.
задача 10917
Положение электрона в потенциальном ящике ограничено интервалом (0<x<l). Определить точки в интервале (0<x<l), в которых плотности вероятности нахождения электрона на первом и втором энергетических уровнях одинаковы? Найти значения плотности вероятности в этих точках. Решение проиллюстрировать графиком.
задача 10918
Частица в потенциальном ящике находится в основном состоянии. Какова вероятность w обнаружить частицу в средней трети ящика?
задача 11163
Частица в потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения частицы в интервале l/4<x<l/2?
задача 11215
Частица массой 1·10–9 кг находится в потенциальной яме шириной а. Найти вероятность обнаружения частицы во втором возбужденном состоянии в третьей четверти ямы.
задача 12693
Электрон в атоме водорода описывается в основном состоянии волновой функцией ψ(r) = Се–r/a. Определить отношение вероятностей w1/w2 пребывания электрона в сферических слоях толщиной Δr = 0,01а и радиусами r1 = 0,5а и r2 = 1,5a.
задача 12697
Волновая функция, описывающая 2s - состояние электрона в атоме водорода, имеет вид 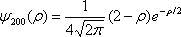 , где ρ — расстояние электрона от ядра, выраженное в атомных единицах. Определить: 1) расстояние ρ1 от ядра, на которых вероятность обнаружить электрон имеет максимум; 2) расстояния ρ2 от ядра, на которых вероятность нахождения электрона равна нулю; 3) построить графики зависимости [ψ200 (ρ)]2 от ρ и ρ2 [ψ200(ρ)]2 от ρ. , где ρ — расстояние электрона от ядра, выраженное в атомных единицах. Определить: 1) расстояние ρ1 от ядра, на которых вероятность обнаружить электрон имеет максимум; 2) расстояния ρ2 от ядра, на которых вероятность нахождения электрона равна нулю; 3) построить графики зависимости [ψ200 (ρ)]2 от ρ и ρ2 [ψ200(ρ)]2 от ρ.
задача 14120
Запишите выражение для вероятности W обнаружения частицы в конечном объеме V, если известна координатная пси-функция частицы ψ(x,y,z).
задача 14121
Волновая функция, описывающая некоторую частицу, может быть представлена в виде 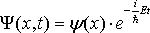 . Покажите, что плотность вероятности нахождения частицы определяется только координатной ψ-функцией. . Покажите, что плотность вероятности нахождения частицы определяется только координатной ψ-функцией.
задача 14140
Электрон находится в одномерной прямоугольной потенциальной яме шириной
задача 14261
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 18,43 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x1, х2) обнаружения частицы в интервале от x1 = 0,3l до x2 = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14293
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 73,72. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от х1 = 0,2l до х2 = 0,3l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14306
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 51,19 эВ. Найти квантовое число n, характеризуются энергетическое состояние частицы. Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от x1 = 0,2l до x2 = 0,3l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14364
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 2,048 эВ. Найти квантовое число п, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, x2) обнаружения частицы в интервале от x1 = 0,3l до х2 = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14365
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 2,048 эВ. Найти квантовое число п, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, x2) обнаружения частицы в интервале от x1 = 0,4l до х2 = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14369
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 37,68эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, х2) обнаружения частицы в интервале от x1 = 0,1l до х2 = 0,2l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14381
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной ямс шириной l = 10–10 м. Энергия частицы Wn = 37,63 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x1, х2) обнаружения частицы в интервале от x1 = 0,2l до х2 = 0,3l. Построить график зависимости от координаты х плотности вероятности |ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14384
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 601,7 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, х2) обнаружения частицы в интервале от x1 = 0,1l до х2 = 0,2l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14527
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 1354 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от х1 = 0,1l до х2 = 0,2l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14580
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 73,72 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x1, x2) обнаружения частицы в интервале от x1 = 0,3l до x2 = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 14621
Частица находится в возбужденном состоянии (n = 4) в потенциальном ящике шириной l. Какова вероятность нахождения частицы в пределах 0<x<l/5? Решение пояснить графически.
задача 16405
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 338,5 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, х2) обнаружения частицы в интервале от х1 = 0,1l до х2 = 0,2l. Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16542
Частица электрон с энергией En = 1354 эВ находится в одномерной прямоугольной бесконечной потенциальной яме шириной l. Найти главное квантовое число n и вычислить вероятность обнаружения частицы Р(х) в интервале от 0,7l до 0,8l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность. Масса электрона mе = 9,1·10–31 кг, ширина потенциальной ямы l = 10–10 м.
задача 16604
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 18,43 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. ВЫЧИСЛИТЬ вероятность Р(x1, х2) обнаружения частицы в интервале от x1 = 0,4l до x2 = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16605
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 73,72. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от х1 = 0,4l до х2 = 0,5l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16607
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 150,4 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от х1 = 0,1l до х2 = 0,2l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16608
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 150,4 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от х1 = 0,2l до х2 = 0,3l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16609
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 940,2 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от x1 = 0,1l до x2 = 0,2l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16610
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 32,76 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от x1 = 0,2l до x2 = 0,3l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16611
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 32,76 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от x1 = 0,3l до x2 = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16612
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 32,76 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от x1 = 0,4l до x2 = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16613
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 8,191 эВ. Найти квантовое число п, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, x2) обнаружения частицы в интервале от x1 = 0,3l до х2 = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16614
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 8,191 эВ. Найти квантовое число п, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, x2) обнаружения частицы в интервале от x1 = 0,4l до х2 = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16615
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 51,19 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от x1 = 0,4l до x2 = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16616
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 61,19 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от x1 = 0,3l до x2 = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16618
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 51,19 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от x1 = 0,3l до x2 = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16620
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 338,5 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от х1 = 0,2l до х2 = 0,3l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16621
Частица электрон с энергией En = 338,4 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0,5l до х2 = 0,6l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
задача 16622
Частица протон с энергией En = 51,19 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0,2l до х2 = 0,4l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
задача 16623
Частица протон с энергией En = 32,76 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0,2l до х2 = 0,3l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
задача 16624
Частица протон с энергией En = 8,191 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0,4l до х2 = 0,6l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
задача 16625
Частица электрон с энергией En = 940,2 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0,2l до х2 = 0,5l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
задача 16626
Частица протон с энергией En = 18,43 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0,4l до х2 = 0,5l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
задача 16627
Частица электрон с энергией En = 150,4 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0,1l до х2 = 0,3l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
задача 16628
Частица протон с энергией En = 2,048 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0,6l до х2 = 0,9l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
задача 16693
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 18,43 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1,х2) обнаружения частицы в интервале от х1 = 0,3l до х2 = 0,4l. Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 16695
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–11 м. Энергия частицы Wn = 8,191 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1,х2) обнаружения частицы в интервале от х1 = 0,3l до х2 = 0,4l. Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
задача 17133
Поток электронов, ускоренны напряжением 199,5 эВ, движется на барьер, имеющий форму прямоугольной ступеньки. Высота первой части ступеньки 199,8 эВ при её ширине 0,4 нм; второй — 199,4 эВ. Полная ширина барьера 0,6 нм. Определить вероятность проникновения электронов за барьер.
задача 17244
Электрон в одномерной прямоугольной потенциальной яме шириной l = 1 нм с бесконечно высокими стенками находится в возбуждённом состоянии с n = 4. Определить: 1) энергию электрона; 2) вероятность обнаружения электрона в первой четверти ямы. Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения частицы в данном состоянии.
задача 17251
Волновая функция ψ(x) = 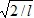 sin(πx/l) описывает основное состояние частицы в бесконечно глубокой прямоугольной потенциальной яме шириной l. Вычислить вероятность нахождения частицы в малом интервале Δl = 0,01l в средней части ямы sin(πx/l) описывает основное состояние частицы в бесконечно глубокой прямоугольной потенциальной яме шириной l. Вычислить вероятность нахождения частицы в малом интервале Δl = 0,01l в средней части ямы 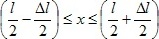
задача 17567
Протон с энергией 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой 10 эВ и шириной 0,1 нм. Определите вероятность прохождения протоном этого барьера. Во сколько раз надо сузить барьер, чтобы вероятность прохождения его протоном была такой же, как для электрона при вышеприведенных условиях.
задача 17687
Частица в потенциальном ящике шириной l находится в низшем возбужденном состоянии. Определить вероятность нахождения частицы в интервале l/4, равноудаленном от стенок ящика.
задача 18066
Частица находится в потенциальном ящике шириной L. Вычислить вероятность того, что частица находится на расстоянии 1/4 от края ящика с точностью 0,08L, если энергия частицы соответствует второму уровню.
задача 18068
Частица находится в потенциальном ящике. Вычислить вероятность найти частицу в первом возбужденном состоянии в первой трети ящика.
задача 20224
Частица в потенциальной яме шириной l находится в возбужденном состоянии. Определить вероятность нахождения частицы в интервале 0 < х < l/4 на втором энергетическом уровне.
задача 20224
Частица оказалась в возбужденном состоянии в потенциальной яме шириной l. Вычислить вероятность того, что частица находится в интервале 0 < х < l/4 на втором энергетическом уровне.
задача 20225
Частица в потенциальной яме шириной l находится в возбужденном состоянии. Определить вероятность нахождения частицы в интервале 0 < х < l/2 на третьем энергетическом уровне.
задача 21057
Частица в потенциальной яме шириной l находится в возбужденном состоянии. Определить вероятность нахождения частицы в интервале 0 < x < l/4 на втором энергетическом уровне.
задача 21377
Электрон находится в одномерной прямоугольной ''потенциальной яме" шириной l с бесконечно высокими "стенками". Определите вероятность W обнаружения электрона в средней трети "ямы", если электрон находится в возбужденном состоянии (n = 3). Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.
задача 22831
Электрон в атоме водорода описывается в основном состоянии волновой функцией Ψ(r) = Се–r/a. Определить отношение вероятностей w1/w2 пребывания электрона в сферических слоях толщиной Δr = 0,01а и радиусами r1 = 0,75а и r2 = 1,25а.
задача 23012
Считая, что поглощенный квант с вероятностью 0,5 порождает пару электрон-дырка, определите количество генерируемых пар при следующих условиях: сила источника света 160 канделл, фотосопротивление находится на расстоянии 0,5 м от источника, длина волны равна 500 нм и площадь фотосопротивления 10 см2.
задача 23729
Во сколько раз отличаются вероятности заполнения электронами состояний с энергией на 5,2·10–2 эВ выше и ниже значения химического потенциала при Т = 300 К?
задача 23841
Прямоугольный потенциальный барьер имеет Ширину 0,1 нм. При какой разности U–Е вероятность прохождения электрона через барьер равна 0,99?
задача 23843
Какова вероятность найти электрон на нижнем уровне зоны проводимости в собственном германии, если температура образца равна: а) 30 К; б) 300 К.
задача 24005
Частица находится в бесконечно глубоком прямоугольном потенциальном ящике, шириной l. Состояние частицу характеризуется волновым числом k = π/l. Какова вероятность W обнаружить частицу в области 0 ≤ x ≤ l/4? Изобразите на графике и заштрихуйте площадь, соответствующую найденному значению вероятности.
задача 90130
Определите вероятность нахождения электрона в потенциальной яме шириной l для наинизшего энергетического состояния в области с координатами l/3≤x≤2/3l.
задача 90140
Частица в потенциальной яме шириной l находится в низшем возбужденном состоянии. Определить вероятность нахождения частицы в интервале l/2, равноудаленном от стенок ямы.
|
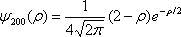 , где ρ — расстояние электрона от ядра, выраженное в атомных единицах. Определить: 1) расстояние ρ1 от ядра, на которых вероятность обнаружить электрон имеет максимум; 2) расстояния ρ2 от ядра, на которых вероятность нахождения электрона равна нулю; 3) построить графики зависимости [ψ200 (ρ)]2 от ρ и ρ2 [ψ200(ρ)]2 от ρ.
, где ρ — расстояние электрона от ядра, выраженное в атомных единицах. Определить: 1) расстояние ρ1 от ядра, на которых вероятность обнаружить электрон имеет максимум; 2) расстояния ρ2 от ядра, на которых вероятность нахождения электрона равна нулю; 3) построить графики зависимости [ψ200 (ρ)]2 от ρ и ρ2 [ψ200(ρ)]2 от ρ.
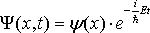 . Покажите, что плотность вероятности нахождения частицы определяется только координатной ψ-функцией.
. Покажите, что плотность вероятности нахождения частицы определяется только координатной ψ-функцией.
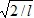 sin(πx/l) описывает основное состояние частицы в бесконечно глубокой прямоугольной потенциальной яме шириной l. Вычислить вероятность нахождения частицы в малом интервале Δl = 0,01l в средней части ямы
sin(πx/l) описывает основное состояние частицы в бесконечно глубокой прямоугольной потенциальной яме шириной l. Вычислить вероятность нахождения частицы в малом интервале Δl = 0,01l в средней части ямы