Заказать решения
Задачи по физике (рус)
Задачі з фізики (укр)
Вопросы по физике:
6 класс Другие предметы
|
обод радиусом вращается с ускорением момент точка скорость колеса найти время
задача 10047
Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой n = 12 с–1, чтобы он остановился в течение времени Δt = 8 с. Диаметр блока D = 30 см. Массу блока m = 6 кг считать равномерно распределенной по ободу.
задача 10047
Блок диаметром D = 30 см и массой m = 6 кг вращается с частотой n = 12 с–1. При каком моменте силы М, приложенному к блоку, он остановится за время Δt = 8 с. Масса блока равномерно распределена по ободу.
задача 12544
Диск радиусом R = 5 см вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением ω = 2At + 5Bt4 (A = 2 рад/с2, В = 1 рад/с5). Определить для точек на ободе диска к концу первой секунды после начала движения: 1) полное ускорение; 2) число оборотов, сделанных диском.
задача 12870
Уравнение вращения колеса радиусом R = 0,5 м имеет вид φ = At + Bt5, где А = 2 рад/с; В = 0,5 рад/с5. Определить полное ускорение в момент t = 1 с точки, находящейся на ободе колеса.
задача 12938
Зависимость угла поворота радиуса вращающегося колеса от времени представлена уравнением φ = 4+10t–3t3. Найти в конце первой секунды вращения угловую скорость колеса, а также линейную скорость и полное ускорение точки на ободе колеса. Радиус колеса 2 см.
задача 13017
Точка А находится на ободе колеса радиусом 69 см, которое катится без скольжения по горизонтальной поверхности со скоростью 5 м/с. Найти полный путь, проходимый точкой A между двумя последовательными моментами ее касания поверхности.
задача 13137
К ободу сплошного однородного диска радиуса R = 0,5 м приложили постоянную касательную силу F = 100 Н. При вращении диска на него действует момент силы трения Mтр = 2 Н·м. Определить массу m диска, если известно, что его постоянное угловое ускорение ε равно 16 рад/с².
задача 13137
Однородный сплошной диск радиусом R = 0,5 м вращается с угловым ускорением ε = 16 рад/с² за счет приложенной к ободу диска постоянной касательной силы F = 100 Н, и момента сил трения Мтр = 2 Н·м. Определить массу m диска.
задача 13306
Линейная скорость v1 точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость v2 точки, находящейся на 6 см ближе к его оси. Определите радиус диска.
задача 13319
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = At2 (А = 0,1 рад/с2). Определите полное ускорение а точки на ободе диска к концу второй секунды после начала движения, если линейная скорость той точки в этот момент равна 0,4 м/с.
задача 13320
Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = At+Bt2 (А = 0,3 м/с2, B = 0,1 м/с3). Определите угол α, который образует вектор полного ускорения а с радиусом колеса через 2 с от начала движения.
задача 13321
Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = At+Bt2 (А = 0,3 м/с2, B = 0,1 м/с3). Определите момент времени, для которого вектор полного ускорения а образует с радиусом колеса угол φ = 4°.
задача 13592
На обод маховика диаметром D = 30 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Трение в подшипниках создает постоянный момент Мтр = 0,1 Н·м. Какую скорость будет иметь груз, спустившись с высоты h = 2 м? Масса маховика М = 20 кг.
задача 13842
К ободу диска массой 5 кг приложена касательная сила 19,6 Н. Какую кинетическую энергию будет иметь диск через 5 с после начала действия силы?
задача 13933
К ободу колеса, которое имеет форму диска радиусом 0,5 м и массой 50 кг, приложенная касательная сила 98 Н. Найти: 1) угловое ускорение колеса; 2) через какое время после начала действия силы колесо будет иметь скорость, соответствующую 100 об/с?
задача 14167
Зависимость угла поворота радиуса вращающегося колеса от времени дана уравнением: φ = 4 + 5t – t2. Найти угловую и линейную скорость вращения колеса, а также полное ускорение точки, лежащей на ободе колеса в конце первой секунды вращения. Радиус колеса 20 см.
задача 14168
Зависимость угла поворота радиуса вращающегося колеса от времени дана уравнением: φ = 4 + 5t2 – t3. Найти в конце первой секунды вращения угловую скорость колеса, а также линейную скорость и полное ускорение точки, лежащей на ободе колеса радиусом 20 см.
задача 14169
Зависимость угла поворота радиуса вращающегося колеса от времени дана уравнением: φ = 4t + 5t2 – t3. Найти в конце второй секунды вращения угловую скорость колеса, а также линейную скорость и полное ускорение точки, лежащей на ободе колеса. Радиус колеса 2 см.
задача 14446
Найти радиус R вращающегося колеса, если известно, что линейная скорость v1 точки, лежащей на ободе, в 2,5 раза больше линейной скорости v2 точки, лежащей на расстоянии r = 5 см ближе к оси колеса.
задача 14459
Найти угловое ускорение ε колеса, если известно, что через время t = 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол α = 60° с вектором ее линейной скорости.
задача 14462
Колесо радиусом R = 5 см вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = А + Bt + Ct2 +Dt3, где D = 1 рад/с3. Для точек, лежащих на ободе колеса, найти изменение тангенциального ускорения Δaτ за единицу времени.
задача 14463
Колесо радиусом R = 5 см вращается так, что зависимость линейной скорости точек, лежащих на ободе колеса, от времени дается уравнением v = At + Bt2, где А = 3 см/с2 и В = 1 см/с3. Найти угол α, составляемый вектором полного ускорения с радиусом колеса в моменты времени t, равные: 0, 1, 2, 3, 4 и 5 с после начала движения.
задача 14464
Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = А + Bt + Ct2 + Dt3, где В = 1 рад/с, С = 1 рад/с2 и D = 1 рад/с3. Найти радиус R колеса, если известно, что к концу второй секунды движения для точек, лежащих на ободе колеса, нормальное ускорение аn = 3,46·102 м/с2.
задача 14629
К ободу однородного диска радиусом R = 0,2 м приложена касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения Mтр = 9,81 Н·м. Найти массу m диска, если известно, что диск вращается с угловым ускорением ε = 100 рад/с2.
задача 14641
Колесо состоит из обода массой 10 кг, диаметром 1 м и шести спиц, масса каждой из которых равна 1 кг. Определить момент инерции колеса относительно оси, проходящей через центр колеса перпендикулярно его плоскости.
задача 14642
Однородный диск массой 3 кг и радиусом 20 см, вращающийся с угловой скоростью 16π рад/с, начинает тормозиться касательной силой 0,05 Н, приложенной к его ободу. Сколько оборотов сделает диск до остановки?
задача 14659
По ободу шкива, насаженного на общую ось с маховым колесом, намотана нить, к концу которой подвешен груз массой m = 1 кг. На какое расстояние h должен опуститься груз, чтобы колесо со шкивом получило скорость, соответствующую частоте колеса n = 60 об/мин? Момент инерции колеса со шкивом J = 0,42 кг·м2, радиус шкива R = 10 см.
задача 15133
Определить полное ускорение в момент времени 3 с точки, находящейся на ободе колеса радиусом 0,5 м, вращающегося согласно уравнения: φ = At + Bt3, где А = 2 с–1, В = 0,2 с–2, φ — угол поворота радиуса колеса. Считая, что вращение колеса происходит в горизонтальной плоскости, изобразить векторы скоростей и ускорений (линейных и угловых), в указанный выше момент времени.
задача 15419
К ободу однородного диска радиусом r = 0,2 м приложена постоянная касательная сила F = 100 Н. При вращении на диск действует сила трения, момент которой М = 5 Н·м. Диск вращается с постоянным угловым ускорением α = 100 рад·с–2. Определить массу диска.
задача 15452
Тело начинает движение из состояния покоя и вращается с постоянным угловым ускорением ε = 0,04 с–2. Через сколько времени точка, принадлежащая этому телу, будет иметь ускорение, направленное под углом 45° к ее скорости?
задача 16059
К ободу однородного диска радиусом 0,2 м приложена касательная сила 10 Н. Найти массу диска, если известно, что диск вращается с угловым ускорением 10 рад/с2.
задача 16129
Маховик массой 4 кг свободно вращается вокруг горизонтальной оси, проходящей через его центр, делая 720 об/мин. Массу маховика можно считать распределенной по его ободу радиусом 40 см. Через 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое делает маховик до полной остановки.
задача 16131
Определить период колебаний переднего колеса велосипеда, поднятого в вертикальное положение. Колесо состоит из обода, массу которого m1 = 3 кг можно считать равномерно распределенной по окружности с радиусом R = 35 см и из укрепленного на ободе вентиля (m2 = 50 г). Моментом инерции спиц и втулки пренебречь.
задача 16710
Колесо радиуса R движется горизонтально со скоростью v0 и вращается с угловой скоростью ω. Точка А на ободе (рис. 8) описывает в пространстве некоторую траекторию. Найти радиус ее кривизны ρ в момент, когда точка находится на уровне центра колеса.
задача 17985
Шкив колеса имеет горизонтальную ось. На обод шкива намотан шнур, к свободному концу которого подвешена гиря массой m, Считая массу шкива равномерно распределенной по ободу, найти натяжение Т шнура при движении груза. Трением и массой шнура пренебречь.
задача 18961
Однородный диск радиуса 0,10 м и массы 5,0 кг вращается вокруг своей оси с угловой скоростью ω = A +Bt, где В = 8 рад/с2. Найдите величину касательной силы, приложенной к ободу диска, считая ее постоянной.
задача 18962
Диск радиуса 20 см и массы 2 кг вращается вокруг своей оси с угловой скоростью ω = 20+8t (рад/с). Найдите касательную силу, приложенную к ободу диска.
задача 19141
К ободу однородного диска радиусом 0,2 м приложена постоянно касательная сила 100 Н. При вращении на диск действует сила трения, момент которой 5 Н·м. Вычислите массу диска, если известно, что он вращается с постоянным угловым ускорением 100 рад/с2, а также кинетическую энергию в момент времени 1 с.
задача 19144
К ободу однородного шара радиусом 0,1 м приложена постоянно касательная сила 50 Н. При вращении на шар действует сила трения, момент которой 4 Н·м. Вычислите массу шара, если известно, что он вращается с постоянным угловым ускорением 80 рад/с2, а также его кинетическую энергию в начальный момент времени.
задача 19176
К ободу однородного цилиндра радиусом 0,3 м приложена постоянно касательная сила 150 Н. При вращении на диск действует сила трения, момент которой 6 Н·м. Вычислите массу тела, если известно, что оно вращается с постоянным угловым ускорением 150 рад/с2, а также его кинетическую энергию в момент времени 1 с.
задача 19609
Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = At + Bt2 (A = 0,3 м/с2, В = 0,1 м/с3). Определите момент времени, для которого вектор полного ускорения a образует с радиусом колеса угол φ = 4°.
задача 19898
К ободу однородного диска радиусом 0,2 м приложена постоянная касательная сила 98,1 Н. При вращении на диск действует момент сил трения
задача 19907
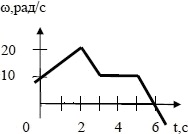
Дан график зависимости угловой скорости от времени для обруча, вращающегося в горизонтальной плоскости относительно вертикальной оси, проходящей через одну из точек на его ободе. Построить график зависимости момента силы, действующей на обруч, от времени. Момент инерции обруча равен 20 кг·м2.
задача 20068
Зависимость угла поворота радиуса (r = 2 м) вращающегося колеса от времени задана уравнением φ = 4+5t–t3. Найти угловую скорость и полное ускорение точки, лежащей на ободе колеса, в конце первой секунды вращения. Каковы средние скорость и ускорение за это время?
задача 20163
Однородный диск массой m и радиусом R начинает вращаться вокруг неподвижной оси, проходящей через центр диска перпендикулярно его плоскости, под действием касательной силы, приложенной к ободу диска. Модуль силы зависит от времени как F = αt2, где α — некоторая положительная постоянная. Найти угловую скорость ω1 диска в момент времени t1 после начала действия силы.
задача 20264
Найти радиус R вращающегося колеса, если известно, что линейная скорость точки v1, лежащей на его ободе, в n = 2,5 раза больше линейной скорости точки v2, лежащей на δх = 6,0 см ближе к оси колеса.
задача 20264
На вращающемся колесе линейная скорость точки v1, лежащей на его ободе, в n = 2,5 раза больше линейной скорости точки v2, лежащей на δх = 6,0 см ближе к оси колеса. Найти радиус R колеса.
задача 20665
Маховик радиусом 1 м вращается по закону φ = t3 – 3t2, рад. Определить нормальное ускорение точки, находящейся на ободе маховика в момент времени, когда касательное ускорение точки обращается в нуль.
задача 20734
Колесо радиусом R = 10 см вращается так, что зависимость угла поворота радиуса колеса от времени задана уравнением φ = 3+2t2+t3, где φ — в радианах, t — в секундах . Найдите для точек, лежащих на ободе колеса: а) линейную скорость, б) нормальное ускорение и в) угловое ускорение ε для момента времени t = 3 с.
задача 21361
К ободу однородного диска радиусом 29 см приложена постоянная касательная сила 63 Н. При вращении на диск действует момент сил трения 2 Н·м. Найти массу диска, если он вращается с постоянным угловым ускорением 70 рад/с.
задача 21388
К ободу диска радиусом R = 5 см приложена касательная сила F = 19,6 Н. Какой момент импульса будет иметь диск через время 5 с после начала действия силы?
задача 22920
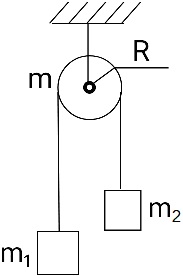
Два груза m1 = 1 кг и m2 = 0,5 кг связаны легким шнуром, перекинутым через блок. Блок радиусом R = 10 см вращается с угловым ускорением β = 20 рад/с2. Найти массу блока, если она равномерно распределена по его ободу.
задача 23143
Радиус-вектор материальной точки в начальный момент времени r(0) = 2i – 4j + k, скорость зависит от времени по закону v(t) = 2ti – (4 – t)j + k. Найти величину перемещения материальной точки за время от t = 3 сек до t = 5 сек.
задача 23954
Колесо начинает вращаться вокруг своей оси с угловым ускорением ε = 4 рад/c2. Через какой промежуток времени угол между вектором скорости и вектором ускорения точки на ободе колеса станет равным α = 45°?
задача 23986
Время разгона автомобиля до скорости 130 км/ч составляет 13 секунд. Каковы в момент окончания разгона автомобиля центростремительное, тангенциальное и полное ускорения точек, расположенных на ободе колеса при разгоне (относительно автомобиля)? Диаметр колеса равен 0,5 м.
задача 23991
Диск находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением ε = 0,25 рад/с2. Через сколько времени угол между векторами скорости и ускорения составит α = 45°?
задача 24047
Обруч начинает вращаться так, что полное ускорение точек обода а = 2,0 м/с2, а тангенциальное ускорение аτ = const. Чему равен момент силы и момент импульса в момент времени, когда скорость обруча V = 0,6 м/с. Масса обруча m = 0,50 кг, радиус r = 0,25 м. Ось вращения проходит через центр обруча перпендикулярно его плоскости.
задача 24263
Колесо радиусом R = 0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением ω = 2At + 5Bt4 (А = 2 рад/с2 и В = 1 рад/с5). Определите полное ускорение точек обода колеса через t = 1 с после начала вращения и число оборотов, сделанных колесом за это время.
задача 24307
К ободу колеса, имеющего форму диска, радиусом R = 0,5 м и массой m = 50 кг приложена касательная сила в 10 Н. Найти: 1) угловое ускорение колеса; 2) через сколько времени после начала действия силы колесо будет иметь скорость, соответствующую 100 об/с?
задача 24797
Колесо вращается по закону φ = 4 + 5t – t3. Найти линейную скорость в конце второй секунды, полное ускорение точек находящегося на ободе колеса радиусом 2 см.
задача 24903
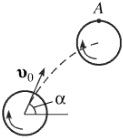
Диск радиуса R, вращающийся вокруг своей оси с угловой скоростью ω, брошен под углом α к горизонту со скоростью v0. Точка A на ободе описывает в пространстве некоторую траекторию (рис. 1.7). Найти радиус ее кривизны ρ в момент наибольшего подъема, если точка A находится при этом над центром колеса.
задача 26296
К ободу диска радиусом R = 0,5 м приложена касательная сила F = 100 Н, сообщающая ему угловое ускорение ε = 7,8 рад/c2. Определить массу колеса m и время t, в течении которого колесо приобретает скорость, соответствующую частоте n = 50 об/c.
задача 26685
Какую работу нужно произвести, чтобы маховику массой m = 0,6 т, распределенной по ободу с диаметром D = 1,6 м, сообщить вращение с частотой n = 240 мин–1?
задача 40540
Точка А находится на ободе колеса радиусом 23 см, которое катится без скольжения по горизонтальной поверхности со скоростью 5 м/с. Найти полный путь, проходимый точкой А между двумя последовательными моментами ее касания поверхности.
задача 40540
По горизонтальной поверхности катится без скольжения колесо радиусом 23 см со скоростью 5 м/с. Точка А находится на ободе колеса. Вычислить полный путь, который проходит точка А между двумя последовательными моментами ее касания поверхности.
задача 40551
Найти полное ускорение в момент времени t = 3 c точки, находящейся на ободе колеса радиусом R = 0,5 м, вращающегося согласно уравнению φ = Аt + Вt3, где А = 2 рад/с, В = 0,2 рад/с3.
задача 40551
Угол поворота колеса радиусом R = 0,5 м зависит от времени согласно уравнению φ = Аt + Вt3, где А = 2 рад/с, В = 0,2 рад/с3. Для точки, расположенной на ободе колеса, определить полное ускорение для момента времени t = 3 c.
задача 40606
Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = At + Вt2 (А = 0,3 м/с2, В = 0,1 м/с3). Определить момент времени, для которого вектор полного ускорения a образует с радиусом колеса угол φ = 45°.
задача 40606
Зависимость линейной скорости точек обода диска от времени задана уравнением v = At + Вt2 (А = 0,3 м/с2, В = 0,1 м/с3). Радиус диска R = 10 см. Найти момент времени, для которого вектор полного ускорения a образует угол φ = 45° с радиусом колеса.
задача 40625
Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе колеса, в 4 раза больше линейной скорости точки, находящейся на 28 см ближе к оси колеса.
задача 40625
Отношение линейной скорости точки, лежащей на ободе вращающегося колеса, к линейной скорости точки, находящейся на 28 см ближе к оси колеса, равно 4. Найти радиус колеса.
задача 40626
Линейная скорость v1 точки, находящейся на ободе вращающегося диска, в четыре раза больше, чем линейная скорость v2 точки, находящейся на 28 см ближе к его оси. Определите радиус диска.
задача 40626
На ободе вращающегося диска находится точка, линейная скорость v1 которой в четыре раза больше, линейной скорости v2 точки, которая находится на 28 см ближе к центру диска. Определить радиус диска.
задача 40642
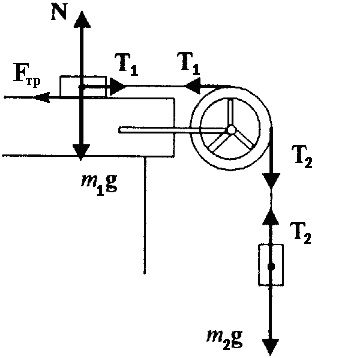
Массы грузов, показанных на рисунке, m1 = 1,5 кг, m2 = 2 кг, масса блока m3 = 1 кг. Коэффициент трения между грузом m1 и горизонтальной поверхностью стола, по которому этот груз движется, равен μ = 0,2. С каким ускорением движутся грузы?
задача 40642
Грузы m1 = 1,5 кг и m2 = 2 кг соединены нитью, лежащей на ободе блока массой m3 = 1 кг. Груз m1 движется с коэффициентом трения равен μ = 0,2. Определить ускорение движения грузов?

задача 40714
На одном валу насажены два колеса с различными диаметрами 16 см и 4 см вращающимися с постоянным угловым ускорением, равным 4 рад/с2. Определить линейные скорости на ободах колес и угловую скорость вращения в конце 2-ой секунды после начала движения.
задача 40714
На вал, вращающийся с постоянным угловым ускорением 4 рад/с2, насажены два колеса с диаметрами 16 см и 4 см. Определить линейные скорости точек на ободах колес и угловую скорость вращения вала через 2 секунды после начала движения.
задача 40787
Маховик, массу которого m = 5 кг можно считать распределенной по ободу радиуса r = 20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой 720 мин–1. При торможении маховик останавливается через промежуток времени Δt = 20 с. Найти число оборотов N, которое сделает маховик до полной остановки.
задача 40819
Сравните кинетическую энергию диска, вращающегося вокруг неподвижной оси и катящегося по горизонтальной плоскости. Линейная скорость точек на ободе диска одинакова.
задача 40878
В центре горизонтальной платформы, которая может свободно вращаться вокруг вертикальной оси, стоит человек и держит велосипедное колесо, вращающееся с угловой скоростью 10 рад/с. Ось колеса расположена вертикально и совпадает с осью платформы. С какой скоростью начнет вращаться платформа, если колесо повернуть вокруг горизонтальной оси на 90°? Момент инерции человека и платформы 6 кг·м2, диаметр колеса 70 см, масса обода колеса 6 кг.
|




