напряженность электрического поля равномерно заряженного тонкого линейная плотность заряда определить расстояние найти радиус
задача 10221
Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда τ = 200 пКл/м. Определить потенциал φ поля в точке пересечения диагоналей.задача 10221
Определить потенциал φ пoля в точке пересечения диагоналей тонкой квадратной равномерно заряженной рамки, если линейная плотность заряда τ = 200 пКл/м.задача 10692
Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда τ = 100 пКл/м. Определить потенциал φ поля в точке пересечения диагоналей.задача 11001
Определить линейную плотность заряда равномерно заряженного тонкого стержня длиной l = 10 см, если на продолжении оси на расстоянии a = 15 см от его середины напряженность электрического поля равна E = 1 кВ/м.задача 11183
С помощью теоремы Гаусса рассчитать поле заряженной с линейной плотностью λ длинной нити.задача 11666
Тонкая нить длиной l = 20 см равномерно заряжена с линейной плотностью τ = 10 нКл/м. На расстоянии а = 10 см от нити, против ее середины, находится точечный заряд Q = 1 нКл. Вычислить силу F, действующую на этот заряд со стороны заряженной нити.задача 12099
Определить силу взаимодействия бесконечной плоскости и тонкого диска диаметром 6 см, если они заряжены с одинаковой плотностью 3 нКл/см2.задача 12131
Два коаксиальных цилиндра несут на себе равномерно распределенный заряд с поверхностными плотностями σ1 и σ2. Используя теорему Гаусса определить напряженность электрического поля в зависимости от расстояния до оси r. Принять σ1 = σ, σ2 = -σ, где σ = 10 нКл/м2. Радиусы цилиндров R1 = R и R2 = 2R, где R = 10 см. Построить график зависимости напряженности Е(r).задача 12214
Две длинные прямые параллельные нити находятся на расстоянии d = 5 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями t1 = –5 нКл/см и t2 = 10 нКл/см. Определить напряженность электрического поля Е в точке, удаленной от первой нити на расстояние r1 = 3 см и от второй на расстояние r2 = 4 см.задача 12317
Поверхностная плотность заряда бесконечной равномерно заряженной плоскости равна 30 нКл/м2. Определить поток вектора напряженности через поверхность сферы диаметром 15 см, рассекаемой этой плоскостью пополам.задача 12318
Поверхностная плотность заряда на бесконечной равномерной заряженной плоскости равна 3·10–10 Кл/м2. Вычислить поток вектора напряженности через поверхность сферы диаметром 1 м, рассекаемой этой плоскостью пополам.задача 13298
Чему равен потенциал электрического поля, созданного двумя равномерно заряженными сферами (радиусы r = 0,12 м, заряды по 32·10–10 Кл) в точке В (см рис. 14.1), если O1O2 = 4r, O2В = 1,5r. Найти напряженность поля в этой же точке.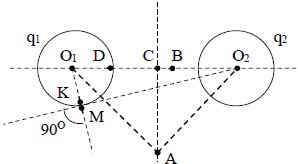
задача 13405
Кольцо радиусом r = 5 см из тонкой проволоки равномерно заряжено с линейной плотностью τ = 14 нКл/м. Определите напряженность поля на оси, проходящей через центр кольца, в точке, удаленной на расстоянии а = 10 см от центра кольца.задача 13405
Кольцо из тонкой проволоки радиусом r = 5 см равномерно заряжено с линейной плотностью τ = 14 нКл/м. Определите напряженность поля в точке, расположенной на нормали к плоскости кольца, проходящей через его центр, и удаленной на расстоянии а = 10 см от центра кольца.задача 13563
Два равномерно заряженных шара с зарядами q1 = –46·10–9 Кл и q2 = 46·10–9 Кл и радиусами 5 см находятся в вакууме так, что расстояние между их центрами O1O2 = 20 см (см рис. 14.1.). Найти напряженность электрического поля в точке В, которая расположена так, что ВО2 = 7,5 см. С какой скоростью упадет протон на поверхность первого шара, если его поместить предварительно в точку В?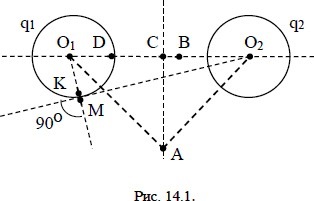
задача 14105
Шар радиуса R = 10 см равномерно заряжен с объемной плотностью ρ = 10–6 Кл/м3. Определить разность потенциалов в двух точках, лежащих на радиальной прямой и удаленных от центра шара на расстоянии S1 = 2 см и S2 = 4 см.задача 14158
Проводник из тонкой проволоки (см. рис.), равномерно заряжен с линейной плотностью τ = 5,5 нКл/м. Определить напряженность электрического поля в т.O, если r = 7 см.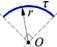
задача 14590
Электрическое поле создано бесконечно длинной равномерно заряженной нитью с отрицательной линейной плотностью заряда τ и положительным точечным зарядом q. Точки 1 - 4 лежат в плоскости, проходящей через нить и заряд q. Вектор градиента потенциала суммарного поля направлен влево и расположен перпендикулярно нити в точке под номером ....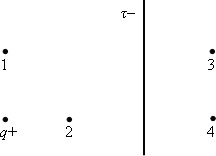
задача 14608
Два коаксиальных цилиндра несут на себе равномерно распределенный заряд с поверхностными плотностями σ1 и σ2. Используя теорему Гаусса, определить напряженность электрического поля в зависимости от расстояния до оси r. Принять σ1 = –σ, σ2 = –2σ, где σ = 10 нКл/м2. Радиусы сфер R1 = R и R2 = 5R, где R = 10 см. Построить график зависимости напряженности E(r).задача 14772
К вертикальной бесконечной равномерно заряженной плоскости прикреплена нить с одноименно заряженным шариком. Как изменится угол отклонения нити при равновесии, если заряд и массу шарика удвоить?задача 14793
На оси равномерно заряженного кольца с зарядом +|q| в точке С закреплен маленький шарик с таким же зарядом.
В точку В (АВ = ВС) поместили положительно заряженную частицу. Определить направление вектора ее ускорения.
задача 14794
Диэлектрический шар (ε>1), заряженный по объему равномерно и положительно, расположен в вакууме. Как изменяются с увеличением расстояния от центра шара напряженность и потенциал электрического поля?задача 14795
График ОАВ на рисунке представляет зависимость E(R) поля равномерно и положительно заряженного шара.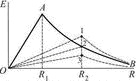
Каким станет график, если радиус шара увеличить от R1 до R2, сохранив заряд шара неизменным?
задача 14800
Вблизи бесконечно длинной равномерно заряженной нити H расположен равномерно заряженный короткий стержень.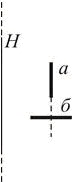
Сравнить силы, действующие на стержень в положениях а и б.
задача 14812
В равномерно заряженном по объему пространстве выделена кубическая поверхность, вписанная в сферу. Определить отношение потоков вектора напряженности электрического поля через эти поверхности.задача 14819
Вблизи равномерно заряженной нити мысленно построим замкнутую поверхность, имеющую форму цилиндра, соосного с нитью. Как изменится поток вектора напряженности электрического поля через полную поверхность цилиндра, если наклонить нить, сохранив пересечение нити с основаниями цилиндра?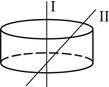
задача 14839
Электрон движется равномерно по плоской круговой траектории. Отличны ли от нуля в центре этой окружности: а) средняя индукция магнитного поля, б) средняя напряженность электрического поля.задача 14959
Тонкое однородное равномерно заряженное кольцо вращается с постоянной угловой скоростью вокруг оси, совпадающей с одним из диаметров кольца. Линейная плотность заряда τ, линейная плотность кольца ρ. Вычислить отношение магнитного момента кольца к моменту импульса.задача 15163
По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью λ. Определить напряженность электрического поля Е, создаваемого таким распределением зарядов в точке, совпадающей с центром кривизны дуги. Длина l нити составляет одну треть длины окружности.задача 15715
Два коаксиальных цилиндра несут на себе равномерно распределенный заряд с поверхностными плотностями σ1 = 3σ и σ2 = –σ, где σ = 10 нКл/м2. Определить напряженность электрического поля в зависимости от расстояния до оси r. Радиусы цилиндров R и 2R, где R = 10 см. Найти зависимость E(r), вычислить E(R1), E(R2), если R1 = 1,5R, R2 = 3R. Построить график зависимости напряженности Е(r).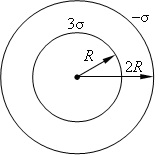
задача 15915
По поверхности сферического сегмента равномерно распределен электрический заряд с поверхностной плотностью σ = 60 нКл/м2. Определить в точке О, совпадающей с центром сферы напряженность Е электрического поля. Угол θ = π/4.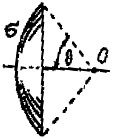
задача 15916
По поверхности сферического сегмента равномерно распределен электрический заряд с поверхностной плотностью σ = 60 нКл/м2. Определить в точке О, совпадающей с центром сферы: 1) напряженность Е электрического поля; 2) силу F, действующую на точечный заряд q = 20 нКл. Угол θ = π/4.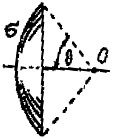
задача 16066
Точечный заряд q = 10 нКл находится в поле, созданном прямой бесконечной нитью, равномерно заряженной с линейной плотностью τ = 0,2 нКл/см. Определить силу F, действующую на заряд, если его расстояние от нити r = 10 см.задача 16069
Пользуясь принципом суперпозиции электрических полей вычислить напряженность поля в точке, лежащей на перпендикуляре, восстановленном в центре заряженного диска, на расстоянии равном его радиусу. Поверхностная плотность заряда на диске 5 мКл/м2, радиус диска 0,05 м.задача 16230
Две большие параллельные пластины, равномерно заряженные одинаковыми зарядами, находятся на близком расстоянии друг от друга. Поток вектора напряженности через квадрат со стороной 20 см, расположенный вне пластин параллельно им, равен 40 В·м. Найдите поверхностную плотность заряда на каждой из пластин. ε0 = 8,85·10–12 Кл2/(Н·м2).задача 16295
Бесконечная равномерно заряженная нить с линейной плотностью заряда 5·10–8 Кл/см расположена горизонтально. Под ней на расстоянии 3 см находится в равновесии шарик массой 0,01 г. 1) Определить заряд шарика. 2) Какую работу нужно совершить, чтобы переместить шарик на расстояние 6 см от нити?задача 16296
Бесконечная равномерно заряженная нить с линейной плотностью заряда 3·10–8 Кл/см расположена горизонтально. Под ней на расстоянии 2 см находится в равновесии шарик массой 0,01 г. 1) Определить заряд шарика. 2) Какую работу нужно совершить, чтобы переместить шарик на расстояние 4 см от нити?задача 16317
Найти модуль вектора напряженности электрического поля, создаваемого бесконечной плоскостью, заряженной равномерно с поверхностной плотностью заряда σ < 0.задача 16443
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ1 = –120 нКл/м2 и σ2 = 60 нКл/м2. Используя теорему Гаусса, найти зависимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, удаленной от оси цилиндров на расстояние r = 1,5R. Построить график зависимости Е(r).задача 16544
Электрическое поле создано квадратом, заряженным по периметру с линейной плотностью τ = 10–7 Кл/м. Сторона квадрата a = 0,2 м. Рассчитать напряженность поля в точке, лежащей на оси квадрата, на расстоянии S = 0,1 м от его центра.задача 17115
Заряд q = 10 нКл равномерно распределен по дуге окружности, радиус которой r = 1 см, с углом раствора равным π рад. Определить напряженность электрического поля в центре окружности.задача 17283
Кольцо радиуса R = 0,15 м равномерно заряжен положительным зарядом Q = 10–6 Кл. Найти силу, с которой заряженное кольцо действует на точечный заряд +q = 10–8 Кл, находящийся на оси кольца, на расстоянии h = 0,1 м от центра кольца?задача 17296
Шар радиуса R заряжен однородно с объемной плотностью ρ. Найти напряженность поля Е и потенциал φ для точек внутри шара.задача 17308
Две параллельные бесконечные плоскости заряжены: одна с плотностью σ1 = +4,42·10–10 Кл/м2, другая с плотностью σ2 = –8,84·10–10 Кл/м2 (рис. 3.7). Найти напряженность поля Е для каждой из областей A, B и С.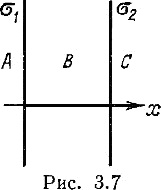
задача 17308
Две параллельные бесконечные плоскости заряжены: одна с плотностью σ1 = +4,42·10–10 Кл/м2, другая с плотностью σ2 = –8,84·10–10 Кл/м2 (рис. 3.7). Найти напряженность поля Е для каждой из областей A, B и С.
задача 17349
Рассчитать потенциал в центре сферы радиуса R = 0,04 м, равномерно заряженной по объему с объемной плотностью ρ = 10–9 Кл/м2.задача 17354
Две бесконечно длинные параллельные нити находятся на расстоянии a = 5 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями τ1 = –5·10–9 Кл/м и τ2 = +10·10–9 Кл/м. Определить напряженность электрического поля в точке, удаленной от первой нити на расстоянии b = 3 см и от второй — c = 4 см.задача 17425
Какую работу надо совершить, чтобы перенести заряд q = 5 нКл из центра равномерно заряженного кольца радиусом R = 10 см, с линейной плотностью τ = 200нКл/м в точку, расположенную на оси кольца на расстоянии 20 см от его центра?задача 17438
Электрическое поле создано двумя бесконечными параллельными равномерно заряженными пластинами с поверхностными плотностями заряда +40 нКл/м2 и –80 нКл/м2. Определить напряженность поля между пластинами.задача 17675
Шар радиусом R заряжен однородно с объёмной плотностью ρ. Найти напряженность поля для точек внутри и вне шара.задача 17784
Электрическое поле создано заряженными кольцом и нитью, лежащей на оси кольца с одной его стороны. Радиус кольца равен 0,2 м, длина нити равна 0,3 м. Линейные плотности зарядов кольца и нити одинаковые и равны 0,4·10–7 Кл/м. Определить напряженность электрического поля в точке, лежащей на оси кольца по другую его сторону на расстоянии 0,4 м от центра.задача 18094
Определить напряженность поля Е в центре полусферы, равномерно заряженной поверхностной плотностью заряда σ.задача 18095
Тонкое кольцо радиуса R равномерно заряжено зарядом q. Найти зависимость Е(r) напряженности поля Е на оси кольца, как функцию расстояния r до его центра. Определить максимальное значение напряженности Ет и соответствующее ему расстояние rm. Зависимость Е(r) изобразить графически.задача 18867
Система состоит из тонкого проволочного кольца и полубесконечной нити. Конец нити совпадает с центром кольца. Радиус кольца R. Кольцо заряжено зарядом q, а нить заряжена равномерно с линейной плотностью λ. Найти силу их взаимодействия.задача 19147
Две параллельные нити, расположенные на расстоянии 6 см, равномерно заряжены с линейными плотностями +3·10–8 Кл/м и –2·10–8 Кл/м соответственно. Вычислить напряжённость электрического поля и силу, действующую на заряд –5·10–8 Кл в точке, расположенной на расстоянии 4 см от первой и 3 см от второй нитей.задача 19200
Длинный цилиндр радиусом R равномерно заряжен с объемной плотностью ρ. Найти потенциал φ поля внутри цилиндра на расстоянии r от его оси. Принять φ(0) = 0.задача 19278
Тонкое кольцо, радиус которого R = 10 см, заряжено линейной плотностью τ = 8 нКл/м. Определить модуль Е напряженности электрического поля в точках, лежащих: а) на оси кольца на расстоянии x = 15 см от его центра; б) в центре кольца; в) на большом расстоянии х >> R от кольца. На каком расстоянии xmax напряженность поля достигнет максимального значения? Вычислить это значение.задача 19297
Длинный прямой провод, расположенный в вакууме, имеет заряд равномерно распределенный по длине. Линейная плотность заряда τ = 10–9 Кл/м. Определить напряженность Е электрического поля на расстоянии 1,5 м от провода в средней его части.задача 19298
Бесконечная очень тонкая прямая нить заряжена однородно с линейной плотностью τ. Используя теорему Гаусса найти модуль напряженности поля Е, как функцию расстояния r от нити.задача 19881
Две бесконечно длинные равномерно заряженные нити с линейной плотностью заряда τ = 5·10–9 Кл/м расположены на расстоянии а = 0,1 м друг от друга. Найти напряженность электрического поля в точке, находящейся на расстоянии b = 0,1 м от каждой нити.задача 19894
Две длинные коаксиальные трубки радиусами R1 = 2 см и R2 = 4 см заряжены равномерно с линейной плотностью зарядов τ1 = 1 нКл/м и τ2 = –0,5 нКл/м соответственно. Пространство между трубками заполнено воздухом. Определить напряженность поля в точках, отстоящих от оси трубок на расстояниях 3 см и 5 см.задача 19996
Определить плотность энергии электрического поля, созданного в вакууме равномерно заряженной прямой длинной нитью с линейной плотностью заряда τ = 3·10–8 Кл/м, в точке, расположенной на расстоянии r0 = 10 cм от середины нити.задача 20177
Бесконечная равномерно заряженная нить и шар расположены, как показано на рис. 8. Заряд шара 10–9 Кл; линейная плотность заряда на нити 5·10–10 Кл/см; а = 10 см. Окружающая среда — воздух. Определить: напряженность поля в точках A и В; работу перемещения заряда 10–8 Кл из точки А в точку В. Считать, что расположение зарядов не нарушено взаимодействием.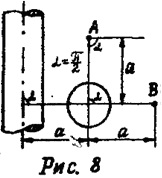
задача 20178
Бесконечно большая равномерно заряженная плоскость и параллельная ей длинная нить расположены, как показано на рис. 11 (перпендикулярно плоскости чертежа); а = 20 см; поверхностная плотность заряда плоскости 10–6 Кл/м2; линейная плотность заряда нити 10–6 Кл/м. Определить: напряженность поля в точках A и В; работу перемещения заряда 10–7 Кл из точки A в точку В. Считать, что распределение зарядов не нарушено взаимодействием.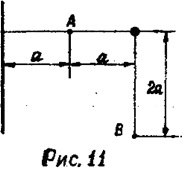
задача 20343
Определить поле в центральной точке А равномерно заряженного по объему полушара радиуса R. Общий заряд полушара равен Q/2.задача 20453
Тонкий стержень равномерно заряжен зарядом q = 1 нКл. Определить напряженность поля в точке, отстоящей от концов стержня на расстоянии r = 20 см и от его середины на расстоянии h = 15 см.задача 20838
Поле создано заряженным по периметру с линейной плотностью х = 10–7 Кл/м квадратом. Сторона квадрата а = 0,2 м. Рассчитать напряженность электрического поля в центре квадрата.задача 20839
Кольцо из проволоки радиуса R = 0,1 м равномерно заряжено зарядом Q = 10–9 Кл. На каком расстоянии на оси кольца от его центра напряженность электрического поля будет максимальной.задача 20844
Поле создается частью сферы радиуса R, получаемой между двумя параллельными плоскостями, одна из которых рассекает сферу пополам, вторая проходит на расстоянии R/2 от первой. Поверхностная плотность сферы равна σ = 10–9 Кл/м2. Параллельные плоскости не заряжены. Вычислить напряженность электрического поля в центре сферы.задача 20999
Электрический заряд с линейной плотностью τ = 10 нКл/м равномерно распределен по тонкой нити изогнутой в кольцо радиусом R. После удаления 1/4 части кольца напряженность поля в центре кривизны стала составлять Е = 4,24 кВ/м. Рассчитайте радиус кольца R. Найдите потенциал поля φ в его центре.задача 21198
Электрическое поле создано длинным цилиндром радиуса 1 см, равномерно заряженным с линейной плотностью заряда 20 мКл/м. Найдите разность потенциалов двух точек этого поля, находящихся на расстояниях 0,5 см и 2 см от оси цилиндра в средней его части.задача 21234
На тонком кольце равномерно распределен заряд с линейной плотностью заряда τ = 20 нКл/см. Радиус кольца R = 5 см. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд q = 40 нКл. Определить силу, действующую на точечный заряд со стороны заряженного кольца, если он удален от центра кольца на: 1) а1 = 10 см; 2) а2 = 2 м.задача 21249
Равномерно заряженный с линейной плотностью заряда λ отрезок нити имеет длину L. Найдите электрическую напряженность в точке А, расположенной на расстоянии L/4 от отрезка напротив его середины.задача 21444
Длинный прямой металлический цилиндр радиуса R заряжен с линейной плотностью заряда λ. Какова зависимость объемной плотности энергии электрического поля от расстояния r до оси цилиндра (ε = 1)?задача 21618
Шар равномерно заряжен с объемной плотностью 0,70 нКл/м3. Найти потенциал его электрического поля как функцию расстояния от центра.задача 21783
Две длинные прямые параллельные нити, заряженные равномерно с линейной плотностью λ, находятся на расстоянии d друг от друга. Найти напряженность поля в точке, лежащей на расстоянии d от обеих нитей.задача 21787
Сплошной шар радиусом 10 см заряжен равномерно зарядом 2 нКл. Найти разность потенциалов между центром шара и точками, лежащими на его поверхности.задача 21888
Процесс электрокопчения состоит в осаждении коптильных компонентов на пищевых продуктах в электрическом поле. Одним из узлов установки для электрокопчения служат два электрода, один из которых является плоскостью, а второй – тонкой проволокой. Считая электроды бесконечно длинными, найти силу, которая действует на каждый метр заряженной проволоки, находящейся в поле плоскости. Считать, что линейная плотность заряда на проволоке 3·10–8 Кл/см, а поверхностная плотность заряда на плоскости 2·10–9 Кл/см2.задача 21937
Электрическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью τ = 1 нКл/см. Какую скорость приобретет электрон, приблизившись под действием поля к нити вдоль линии напряженности с расстояния r1 = 1,5 см до r2 = 1 см?задача 22052
Точечный заряд Q = 20 нКл помещен в центре равномерно заряженного по объему шара радиуса R = 15 см, заряд которого Q = –20нКл, εшара ≈ 1. Определить напряженность поля Е в точках А и В, удаленных от центра шара на расстояниях rA = 20 см и rB = 10 см.задача 22054
Диск радиусом R = 4 см заряжен до поверхностной плотности σ = 2·10–7 Кл/м2. Чему равна напряженность поля в вакууме, созданная заряженным диском в точке, находящейся на перпендикуляре, восстановленном из центра диска на расстояние d = 3 см от него?задача 22068
Кольцо из проволоки радиусом R = 10 см заряжено отрицательно, находится в вакууме и несет заряд Q = –5 нКл. 1) Найти напряженность Е электрического поля на оси кольца на расстоянии L = 0,5 см; 8 см; 10 см; 15 см. Начертить график E = f(L). 2) На каком расстоянии L0 от центра кольца напряженность электрического поля будет максимальной?задача 22929
Бесконечная прямая нить равномерно заряжена с линейной плотностью заряда λ. Найти работу сил поля по перемещению точечного заряда q из точки, находящейся на расстоянии R от нити в точку, находящуюся на расстоянии 2R.задача 23779
Определить напряжённость электростатического поля, создаваемого тонким длинным стержнем, равномерно заряженным с линейной плотностью заряда 20 мКл/м в точке, находящейся в 2 см от стержня.задача 23866
Три плоскопараллельные пластины, расположенные на малом расстоянии друг от друга, равномерно заряжены с поверхностной плотностью σ = 5·10–8 Кл/м2 каждая. Найти напряженность поля в точках, лежащих между пластинами и с внешней стороны. Построить график зависимости напряженности поля от расстояния, взяв за начало отсчета положение первой пластины.задача 23868
Найти объемную плотность энергии w электрического поля на расстоянии r = 2,0 см от бесконечно длинной нити, заряженной с линейной плотностью τ = 4,2 нКл/м.задача 23893
Тонкая проволока, представляющая по форме кольцо радиуса R, заряжена равномерно зарядом q. Найти напряженность поля в центре кольца.задача 23895
Бесконечно длинный цилиндр радиуса R заряжен с объемной плотностью ρ = b/(r2+l2)1/2, l, b — постоянные, r — расстояние от оси цилиндра. Найти E (r).задача 24262
Чему равен потенциал на расстоянии 2 м от равномерно заряженного шарика с зарядом 2·10–8 Кл?задача 24284
Кривые 1 и 2 со ответствуют зависимости модуля напряженности электрического поля на оси равномерно заряженных тонких колец. Определите отношение линейных плотностей зарядов колец τ2/τ1.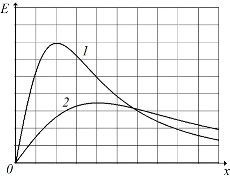
задача 24466
Найти напряженность электростатического поля в центре кривизны тонкого полукольца радиуса R = 8 см и линейную плотность заряда τ на кольце, если известно, что заряд по нему распределен равномерно, а потенциал поля в центре кривизны φ = 31,4 В.задача 24468
Заряд Q = 10–10 Кл равномерно распределен по тонкой нити в форме дуги окружности, длина которой равна 5 см и составляет четверть от длины окружности. Вычислить напряженность и потенциал электрического поля в центре кривизны нити.задача 24606
Заряд 0,5 нКл равномерно распределен по поверхности полого металлического шарика радиусом 2,5 см. Найти потенциал электрического поля в центре, на поверхности шарика и на расстоянии 5 см от центра. Построить график зависимости модуля вектора напряженности поля и потенциала от расстояния до центра шарика.задача 24951
В равномерно заряженной бесконечной пластине вырезали сферическую полость так, как показано на рисунке. Толщина пластины h, объемная плотность заряда ρ. Определите модуль напряженности электрического поля Е в точках А и В, а также исследуйте зависимость Е вдоль прямой ОА от расстояния X до точки О.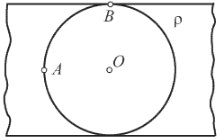
задача 60442
Найти напряженность поля прямой бесконечно длинной нити, равномерно заряженной с линейной плотностью 25 нКл/м, в точке, удаленной от нити на расстояние 37 см.задача 60442
Найти напряженность электрического поля, создаваемого прямой бесконечно длинной равномерно заряженной нитью с линейной плотностью 25 нКл/м, на расстоянии на расстояние 37 см от нити.задача 60481
Поле равномерно заряженной бесконечной плоскости действует в вакууме на заряд 0,2 нКл с силой 22,6 мкН. Определить напряженность электрического поля и поверхностную плотность заряда на плоскости.задача 60481
На заряд 0,2 нКл в вакууме действует поле бесконечной равномерно заряженной плоскости в с силой 22,6 мкН. Найти поверхностную плотность заряда плоскости и напряженность электрического поля.задача 60484
Два бесконечно длинных параллельных провода, расположенных в вакууме заряжены равномерно с линейной плотностью заряда 5•10–8 Кл/м. Расстояние между проводами 0,5 м Определить силу, действующую
Определить силу, действующую  единицу длины провода.
единицу длины провода.