Заказать решения
Задачи по физике (рус)
Задачі з фізики (укр)
Вопросы по физике:
6 класс Другие предметы
|
электроемкость равна между пластинами конденсатор соединить определить найти
задача 11715
Расстояние d между пластинами плоского конденсатора равно 1,33 мм площадь S пластин равна 20 см2. В пространстве между пластинами конденсатора находятся два слоя диэлектриков: слюды толщиной d1 = 0,7 мм и эбонита толщиной d2 = 0,3 мм. Определить электроемкость с конденсатора.
задача 11720
Конденсатор электроемкостью С1 = 0,6 мкФ был заряжен до разности потенциалов U1 = 300 В и соединен со вторым конденсатором электроемкостью С2 = 0,4 мкФ, заряженным до разности потенциалов U1 = 150 В. Найти заряд ΔQ, перетекший с пластин первого конденсатора на второй.
задача 11721
Три одинаковых плоских конденсатора соединены последовательно. Электроемкость С такой батареи конденсаторов равна 89 пФ. Площадь S каждой пластины равна 100 см2. Диэлектрик-стекло. Какова толщина d стекла?
задача 11722
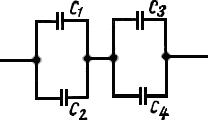
Конденсаторы соединены так, как это показано на рисунке. Электроемкости конденсаторов: C1 = 0,2 мкФ, C2 = 0,1 мкФ, C3 = 0,3 мкФ, С4 = 0,4 мкФ. Определить электроемкость С батареи конденсаторов.
задача 11725
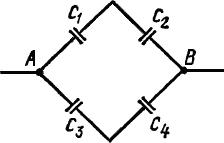
Конденсаторы электроемкостями C1 = 0,2 мкФ, С2 = 0,6 мкФ, С3 = 0,3 мкФ, С4 = 0,5 мкФ соединены так, как это указано на рисунке. Разность потенциалов U между точками А и В равна 320 В. Определить разность потенциалов U1 и заряд Q1на пластинах каждого конденсатора (i = 1, 2, 3, 4).
задача 11726
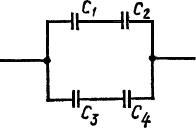
Конденсаторы электроемкостями С1 = 10 нФ, С2 = 40 нФ, С3 = 2 нФ и С4 = 30 нФ соединены так, как это показано на рисунке. Определить электроемкость с соединения конденсаторов.
задача 11727
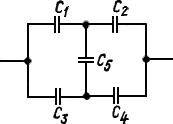
Пять различных конденсаторов соединены согласно схеме, приведенной на рисунке. Определить электроемкость С4, при которой электроемкость всего соединения не зависит от величины электроемкости С5. Принять С1 = 8 пФ, С2 = 12 пФ, С3 = 6 пФ.
задача 11841
Колебательный контур состоит из параллельно соединенных конденсатора электроемкостью С = 1 мкФ и катушки индуктивностью L = 1 мГн. Сопротивление контура ничтожно мало. Найти частоту ν колебаний.
задача 11891
Емкость с плоского конденсатора равняется 1,5 мкФ. Расстояние между пластинами равно 5 мм. Какова будет емкость конденсатора, если на нижнюю пластину поместить лист эбонита толщиной d1 = 3 мм?
задача 11897
Конденсатор электроемкостью С1 = 0,2 мкФ был заряжен, до разности потенциалов U1 = 320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U2 = 450 В, напряжение U на нем изменилось до 400 В. Вычислить емкость С2 второго конденсатора.
задача 12195
Колебательный контур имеет индуктивность L = 1,6 мГц, электроемкость С = 0,04 мкФ и максимальное напряжение Umax на зажимах, равное 200 В. Определить максимальную силу тока Imаx в контуре. Сопротивление контура ничтожно мало.
задача 12519
Гармонические колебания в электрическом контуре начались (t = 0) при максимальном напряжении на конденсаторе Um = 15 B и токе, равном нулю на частоте ν = 0,5 МГц. Электроемкость конденсатора С = 10 нФ. Записать уравнение колебаний тока в контуре.
задача 13790
Плоский конденсатор должен иметь электроемкость 0,2 мкФ и состоять из 46 листов станиоля площадью 62,8 см2 каждый. Определить толщину слоя слюды.
задача 13792
Найти заряд последовательно соединенных конденсаторов, электроемкость которых 2 мкФ и 4 мкФ. Напряжение на батарее конденсаторов 3 В.
задача 14164
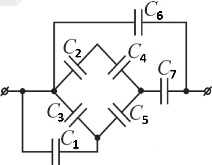
Определить электроемкость батареи конденсаторов (см. рис.): C1 = 1 пФ, C2 = 1 пФ, С3 = 1 пФ, C4 = 4 пФ, C5 = 2 пФ, С6 = 0,82 пФ, С7 = 0,2 пФ.
задача 14826
Батарея последовательно соединенных конденсаторов присоединена к источнику постоянной ЭДС. Пластины одного из конденсаторов раздвигают. Как при этом изменяются: а) электроемкость батареи; б) ее заряд?
задача 14827
Дана батарея последовательно соединенных конденсаторов с электроемкостями и критическими (пробивными) напряжениями. С1 = 2 мкФ, U1 = 3 кВ, С2 = 1 мкФ, U2 = 3,5 кВ, С3 = 4 мкФ, U3 = 1,5 кВ. Пробьет ли эту батарею, если ее подсоединить к источнику ЭДС 7 кВ, а если пробьет, то какой конденсатор пробьет первым?
задача 14832
Батарея конденсаторов АВ заряжена и отключена от источника ЭДС (ключ
задача 15663
Определить электроемкость конденсатора, если диэлектриком является форфоровая пластина толщиной 2 мм, площадь пластины 100 см2, диэлектрическая проницаемость форфора 5.
задача 19132
В идеальном закрытом контуре электроемкость увеличили в 2 раза. Во сколько раз изменится период собственных колебаний?
задача 19457
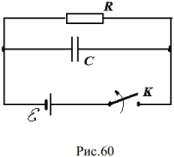
Конденсатор с электроемкостью С = 10 мкФ и резистор сопротивлением R = 1200 Ом соединены параллельно и подключены к источнику, ЭДС которого равна 36 В, через ключ К (рис. 60). В некоторый момент времени ключ К размыкают. Определить заряд на конденсаторе через 0,01 с. Внутренним сопротивлением источника пренебречь.
задача 19542
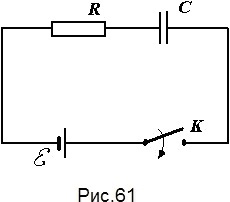
Конденсатор с электроемкостью С = 10,5 мкФ и резистор сопротивлением R = 200 Ом (соединенные последовательно) в некоторый момент времени подключают к источнику, ЭДС которого равна 80 В (рис. 61). Определить энергию поля в конденсаторе через 0,01 с. Внутренним сопротивлением источника пренебречь.
задача 19543
Конденсатор с электроемкостью С = 10,5 мкФ и резистор сопротивлением R = 500 Ом (соединенные последовательно) в некоторый момент времени подключают к источнику, ЭДС которого равна 80 В (рис. 61). Определить энергию поля в конденсаторе через 0,01 с. Внутренним сопротивлением источника пренебречь.

задача 21809
Контур радиоприемника настроен на частоту ν = 9 МГц. Как нужно изменить электроемкость переменного конденсатора этого контура, чтобы приемник был настроен на длину волны λ = 50 м? Скорость электромагнитных волн в вакууме с = 3·108 м/с.
задача 21809
Резонансная частота контура радиоприемника ν = 9 МГц. Во сколько раз нужно увеличить или уменьшить электроемкость переменного конденсатора в контуре, чтобы настроить приемник на длину волны λ = 50 м? Скорость электромагнитных волн в вакууме c = 3·108 м/с.
задача 21889
Вычислить электроемкость тела теленка, считая ее равной емкости электропроводящего шара того же объема (внутри шара e = 1). Среднюю плотность тела теленка принять равной 1 г/см3, а его массу 60 кг.
задача 23867
Электроемкость плоского конденсатора равна С = 111 пФ. Диэлектрик – фарфор (ε = 5). Конденсатор зарядили до разности потенциалов U = 600 В и отключили от источника напряжения. Какую работу А нужно совершить, чтобы вынуть диэлектрик из конденсатора? Трение пренебрежимо мало.
задача 24412
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы.| Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | 1 | – | – | 11 | ~0 | 12 | 1 |
задача 24413
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | ~0 | 10 | 1 | – | – | 12 | ~0 |
задача 24414
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | 1 | – | – | 11 | 1 | – | – |
задача 24415
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | ~0 | 10 | 2 | – | – | – | – |
задача 24416
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | ~0 | – | – | 11 | 1 | – | – |
задача 24417
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | 2 | – | – | – | – | 12 | ~0 |
задача 24418
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | 1 | – | – | 11 | ~0 | 12 | ~0 |
задача 24420
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | ~0 | 10 | ~0 | 11 | ~0 | 12 | 1 |
задача 24421
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | 1 | – | – | – | – | 12 | ~0 |
задача 24422
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | ~0 | 10 | ~0 | 11 | 1 | – | – |
задача 24423
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | – | – | 10 | 1 | – | – | 12 | 1 |
задача 24424
Определите электроемкость системы металлических концентрических сфер. В таблице указаны значения внутренних радиусов Ri и толщин di сфер для соответствующих вариантов. Диэлектрическая проницаемость среды в зазорах между сферами ε = 1. Считать, что с электрической цепью соединены внутренняя и внешняя сферы. Прочерк в ячейке таблицы означает отсутствие соответствующей сферы. | Радиусы Ri и толщины di сфер, см | | R1 | d1 | R2 | d2 | R3 | d3 | R4 | d4 | | 9 | ~0 | 10 | ~0 | 11 | ~0 | 12 | ~0 |
задача 26388
Конденсатор электроемкостью 0,5 мкФ был заряжен до напряжения 350 В. После того как его соединили параллельно со вторым конденсатором, заряженным до напряжения 500 В, напряжение на нем изменилось до 400 В. Вычислить электроемкость второго конденсатора.
задача 26709
Определить электроемкость конденсатора, для изготовления которого использовали ленту алюминиевой фольги длиной 157 см и шириной 9 см. Толщина парафинированной бумаги 0,1 мм, ее относительная диэлектрическая проницаемость равна 2. Какая энергия запасена в конденсаторе, если он заряжен до рабочего напряжения 400 В?
задача 60102
Плоский воздушный конденсатор с площадью пластин 100 см2 заряжен до разности потенциалов 300 В. Определить поверхностную плотность заряда на пластинах, электроемкость и энергию поля конденсатора, если напряженность поля в зазоре между пластинами 60 кВ/м.
задача 60102
Площади пластин плоского воздушного конденсатора 100 см2, разность потенциалов между пластинами 300 В. Напряженность поля в зазоре между пластинами 60 кB/м. Определить электроемкость конденсатора, поверхностную плотность заряда пластин и энергию поля конденсатора.
задача 60104
Резонанс в колебательном контуре с конденсатором электроемкостью 1 мкФ наступает при частоте 4000 Гц. Если параллельно первому конденсатору подключить второй конденсатор, то резонансная частота становится равной 2000 Гц. Определить электроемкость второго конденсатора.
задача 60104
Резонанс в колебательном контуре наступает на частоте 4000 Гц. Электроемкость конденсатора равна 1 мкФ. При параллельном подключении к первому конденсатору второго, резонансная частота снижается до 2000 Гц. Определить электроемкость второго конденсатора.
задача 60389
Коаксиальный электрический кабель состоит из центральной жилы радиусом 1 см и цилиндрической оболочки радиусом 1,5 см, между которыми находится изоляция. Вывести формулу для емкости такого кабеля и вычислить электроемкость кабеля длиной 10 м, если изоляционным материалом служит резина.
задача 60389
Радиус центральной жилы коаксиального электрического кабеля равен 1 см, радиус цилиндрической оболочки 1,5 см. Пространство между ними заполнено изоляцией. Изоляционным материалом служит резина. Вывести формулу емкости такого кабеля и вычислить электроемкость кабеля длиной 10 м.
задача 60390
В цепь переменного тока с действующим значением напряжения 220 В и частотой 50 Гц включены последовательно конденсатор электроемкостью 1 мкФ и реостат с активным сопротивлением 300 Ом. Найти полное сопротивление цепи и действующее значение силы тока.
задача 60390
Действующее напряжение в цепи переменного тока U=220 B, частота 50 Гц. В цепь последовательно включены конденсатор с электроемкостью C=1 мкФ и реостат с активным сопротивлением R=300 Ом. Определить действующую силу тока и полное сопротивление цепи.
задача 60440
Сферический конденсатор состоит из двух тонких концентрических сферических оболочек радиусом 1,5 и 3 см. В пространстве между оболочками находится диэлектрик с диэлектрической проницаемостью 3,2. Вывести формулу для электроемкости такого конденсатора и вычислить его электроемкость.
задача 60440
Сферический конденсатор представляет собой две тонкие концентрические сферы радиусами 1,5 см и 3 см. В пространстве между сферами находится диэлектрик (ε = 3,2). Вывести формулу для электроемкости сферического конденсатора и вычислить его электроемкость.
задача 60441
В цепь переменного тока с действующим значением напряжения 220 В и частотой 50 Гц включены последовательно резистор сопротивлением 100 Ом, конденсатор электроемкостью 32 мкФ и катушка индуктивностью 640 мГн. Найти действующее значение силы тока, сдвиг фаз между силой тока и напряжением и потребляемую мощность.
задача 60441
Резистор сопротивлением R=100 Ом, конденсатор электроемкостью C=32 мкФ и дроссель индуктивностью L=640 мГн включены последовательно в цепь переменного тoкa с действующим напряжением 220B и частотой 50 Гц. Haйти действующее значение силы тока, сдвиг фаз между силой тoкa и напряжением и потребляемую мощность.
задача 70234
Конденсатор электроемкостью 500 пФ составляет с катушкой индуктивности из 1000 витков длиной 40 см и площадью сечения 5 см2 без сердечника колебательный контур. Найти период колебаний такого контура.
|







