Физика и др.
Заказать решения

Задачи по физике (рус)

Задачі з фізики (укр)

Вопросы по физике:
6 класс

Другие предметы

Витамины для ума

Лучшая книга о разуме

бесконечная одномерная потенциальная яма электрон ширина частица энергия стенка высоко находится

задача 10443

Используя соотношение неопределенностей, оценить ширину l одномерного потенциального ящика, в котором минимальная энергия электрона Еmin = 10 эВ.
Решение

задача 10443

Минимальная энергия в одномерном потенциальном ящике электрона равна 10 эВ. С помощью соотношение неопределенностей, оценить ширину l, потенциального ящика.
Решение

задача 10444

Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия α-частицы Emin = 8 МэВ.
Решение

задача 10444

Минимальная энергия альфа-частицы, находящейся в бесконечно глубоком, прямоугольном, одномерном потенциальном ящике, Emin = 8 МэВ. С помощью соотношение неопределенностей оценить ширину l ящика.
Решение

задача 10451

Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l = 0,1 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.
Решение

задача 10451

Ширина бесконечно глубокого, одномерного, прямоугольного потенциального ящика, в котором находится электрон, l = 0,1 нм. Найти наименьшую разность энергетических уровней электрона в электрон-вольтах.
Решение

задача 10452

Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l находится в возбужденном состоянии (n = 3). Определить, в каких точках интервала 0 < х < l плотность вероятности нахождения частицы имеет максимальное и минимальное значения.
Решение

задача 10452

Частица в бесконечно глубокой, прямоугольной, одномерной потенциальной яме шириной l находится на 3-ем возбужденном энергетическом уровне. Определить координаты точек из интервала 0 < х < l, в которых плотность вероятности нахождения частицы имеет максимальное и минимальное значения.
Решение

задача 10454

Частица находится в основном состоянии в бесконечно глубоком, прямоугольном, одномерном потенциальном ящике. Какова вероятность w обнаружить частицу в крайней четверти ящика?
Решение

задача 10458

Электрон находится в бесконечно глубоком, прямоугольном, одномерном потенциальном ящике шириной l. Найти координаты точек в интервале от x = 0 до x = l, в которых плотности вероятности нахождения электрона на 2-ом и 3-ем энергетических уровнях одинаковы? Вычислить плотность вероятности для этих положений. Решение пояснить графиком.
Решение

задача 10458

Электрон находится в бесконечно глубокой, одномерной, прямоугольной потенциальной яме шириной l. Найти координаты точек в интервале от х=0 до х=l, в которых плотности вероятности обнаружения электрона на 2 и 3 энергетических уровнях одинаковы? Найти плотность вероятности для этих положений. Решение пояснить графиком.
Решение

задача 10910

Протон находится в одномерном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия Eмин протона равна 10 МэВ.
Решение

задача 10910

Протон находится в одномерном потенциальном ящике. С помощью соотношения неопределенностей оценить ширину l ящика при условии, что минимальная энергия Eмин протона равна 10 МэВ.
Решение

задача 10913

Используя соотношение неопределенностей, оценить ширину одномерного потенциального ящика, в котором минимальная энергия Емин электрона равна 1 эВ.
Решение

задача 10913

С помощью соотношения неопределенностей оценить ширину одномерного потенциального ящика, для которого минимальная энергия Емин электрона равна 1 эВ.
Решение

задача 10958

Микрочастица массой 10–30 кг находится в одномерной потенциальной яме с вертикальными стенками. Найти отношение разности энергий пятого и четвёртого энергетических уровней к энергии частицы в состоянии с квантовым числом n = 4.
Решение

задача 11216

Электрон находится в одномерной потенциальной яме с вертикальными стенками. Найти отношение разности энергий электрона на втором и третьем энергетических уровнях к подобной разности энергий для микрочастицы массой 2·10–26 кг.
Решение

задача 11217

Микрочастица находится в одномерной потенциальной яме шириной а на четвертом энергетическом уровне. Определить отношение плотностей вероятности обнаружения частицы в середине ямы и на расстоянии а/5 от края ямы.
Решение

задача 11218

Частица массой 6,68·10–27 кг находится в третьем возбужденном состоянии в одномерной прямоугольной потенциальной яме. Максимальное значение плотности вероятности координаты частицы равно 1,7·1010 м–1. Найти в эВ энергию частицы в данном состоянии.
Решение

задача 11220

Используя соотношение неопределенностей, оценить в эВ минимальную энергию микрочастицы (m = 1·10–9 кг), находящейся в одномерной потенциальной яме шириной a = 8 нм.
Решение

задача 11238

Используя соотношение неопределенностей, оценить в эВ минимальную энергию микрочастицы (m = 6,68·10–27 кг), находящейся в одномерной потенциальной яме шириной А = 3,29 нм.
Решение

задача 12108

Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях в интервале L/4 равноудаленном от стенок одномерной потенциальной ямы шириной L.
Решение

задача 12125

Ширина потенциальной ямы L = 3 нм. Чему равна частота излученного фотона при переходе электрона с третьего квантового уровня на первый? Как она изменится при увеличении ширины ямы в три раза?
Решение

задача 12629

В одномерном потенциальном ящике шириной l находится электрон. Вычислить вероятность W нахождения электрона на первом энергетическом уровне в интервале l/4, равноудаленном от стенок ящика.
Решение

задача 12658

Используя соотношение неопределенностей Δx·Δрх ≥ ћ, оцените минимальную энергию Emin протона, находящегося в одномерном потенциальном ящике шириной l = 1
Решение

задача 12862

Частица находится в одномерной бесконечно глубокой потенциальной яме шириной L на втором энергетическом уровне Оценить вероятность нахождения частицы в области, ограниченной координатами х1 = L/4 и x2 = 5L/8. Построить график зависимости |ψn(x)|2 для n = 2 и указать рассматриваемый интервал на чертеже.
Решение

задача 13747

Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в основном состоянии. Определите вероятность обнаружения частицы во второй четверти.
Решение

задача 14194

Электрон находится в бесконечно глубокой одномерной потенциальной яме. Во сколько раз различаются вероятности обнаружения электрона в средней части ямы на отрезке Δx =
Решение

задача 14276

Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 490,2 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x1, х2) обнаружения частицы в интервале от x1 = 0 до х2 = 0,1l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
Решение

задача 14370

Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 37,68 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, х2) обнаружения частицы в интервале от x1 = 0 до х2 = 0,1l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
Решение

задача 14383

Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 601,7 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х1, х2) обнаружения частицы в интервале от x1 = 0 до х2 = 0,1l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
Решение

задача 14526

Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 1354 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от х1 = 0 до х2 = 0,1l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
Решение

задача 14676

Микрочастица с массой m = 10–30 кг находится в одномерной потенциальной яме шириной l = 1 нм и имеет энергию 3,08 эВ. Считая, что энергия частицы много меньше "глубины" ямы, найти графически вероятность ее обнаружения на отрезке от х1 = l/3 до х2 = l/2.
Решение

задача 14750

Микрочастица находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Вычислите отношение вероятностей ω5/ω3 нахождения частицы на отрезке l/3≤x≤l/2 на третьем (n = 3) и пятом (n = 5) энергетических уровнях.
Решение

задача 14895

Электрон находится в одномерной прямоугольной потенциальной яме с очень высокими стенками. Ширина ямы l. Оценить с помощью соотношения неопределенностей силу давления электрона на стенки ямы при минимально возможной его энергии.
Решение

задача 14901

В одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками находится микрочастица. На сколько отличаются вероятности обнаружения частицы ω4–ω3 на отрезке l/3 ≤ x ≤ l/2, если частица находится: 1) на четвертом энергетическом уровне; 2) на третьем энергетическом уровне?
Решение

задача 14902

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится на n-м энергетическом уровне (n = 1). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически.
Решение

задача 14903

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (n = 2). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически.
Решение

задача 14904

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (n = 3). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически.
Решение

задача 14905

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (т.е., на n-м энергетическом уровне). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически. n = 4.
Решение

задача 14906

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (т.е., на n-м энергетическом уровне). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически. n = 5.
Решение

задача 14907

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (т.е., на n-м энергетическом уровне). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически.
Решение

задача 14908

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (т.е., на n-м энергетическом уровне). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически. n = 7.
Решение

задача 14909

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (т.е., на n-м энергетическом уровне). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически. n = 8.
Решение

задача 14910

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (т.е., на n-м энергетическом уровне). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически. n = 9.
Решение

задача 14911

Частица в одномерной прямоугольной "потенциальной яме" шириной L с бесконечно высокими "стенками" находится в возбужденном состоянии (т.е., на n-м энергетическом уровне). Определите, в каких точках "ямы" (0≤x≤L) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически. n = 10.
Решение

задача 15949

Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Найти отношение разности ΔЕn, n+1 соседних энергетических уровней к энергии Еn частицы в трех случаях: 1) n = 2; 2) n = 5; 3) n → ∞.
Решение

задача 16268

Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n = 2). Определите вероятность обнаружения частицы в области (3/8)l < x < (5/8)l.
Решение

задача 16284

Электрон находится в одномерном прямоугольном потенциальном ящике шириной l. Определите среднее значение координаты <x> электрона (0 < x < l ).
Решение

задача 16603

Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 338,5 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность р(х1, х2) обнаружения частицы в интервале от х1 = 0 до х2 = 0,1l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
Решение

задача 16606

Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 150,4 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х1, х2) обнаружения частицы в интервале от х1 = 0 до х2 = 0,4l. 3) Построить зависимость от координаты х плотности вероятности |Ψn(х)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
Решение

задача 16617

Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Энергия частицы Wn = 940,2 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x1, х2) обнаружения частицы в интервале от x1 = 0 до х2 = 0,1l. Построить график зависимости от координаты х плотности вероятности |Ψn(x)|2 обнаружения частицы. Показать на построенной зависимости найденную вероятность.
Решение

задача 16619

Частица электрон с энергией En = 601,7 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10–10 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х1 = 0 до х2 = 0,2l. Построить график зависимости волновой функции Ψn(x) и плотности вероятности |Ψn(x)|2 обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.
Решение

задача 17007

Определите ширину l одномерной прямоугольной "потенциальной ямы" с бесконечно высокими стенками, если при переходе электрона с третьего энергетического уровня на второй излучается энергия ΔЕ = 1 эВ.
Решение

задача 17008

Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками, ширина которой l = 1 нм. Определите наименьшую разность энергетических уровней электрона.
Решение

задача 17012

Вычислить энергию, которая необходима, чтобы перевести частицу, заключенную в потенциальном ящике, с третьего уровня на четвертый. Задачу решить: 1) для электрона при ширине ящика 1 ангстрем и 1 мм; 2) для частицы с массой 1 мкг при ширине ящика 1 мм.
Решение

задача 18062

Электрон находится в бесконечно глубоком одномерном потенциальном ящике шириной L (0 < X < L). Определить вероятность того, что электрон, находящийся в первом возбужденном состоянии, будет обнаружен в интервале 1/4 L < X < 3/4 L.
Решение

задача 18063

Электрон находится в основном состоянии в одномерной потенциальной яме с бесконечно высокими стенками. Оценить силу, с которой электрон действует на стенку ямы, если ее ширина 1 ангстрем.
Решение

задача 18065

В одномерной прямоугольной потенциальной яме шириной 0,3 нм с бесконечно высокими стенками в третьем возбужденном состоянии находится электрон. Определить: 1) минимальную энергию электрона; 2) вероятность обнаружения электрона в средней трети ямы.
Решение

задача 19182

Частица находится в одномерном потенциальном ящике с бесконечно высокими стенками. Пси-функция имеет вид, показанный на рисунке 2.13. Найти вероятность пребывания частицы в области l/8 < х < l/2.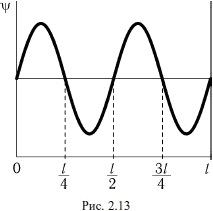
Решение

задача 19183

Частица находится в основном состоянии в одномерной бесконечно глубокой потенциальной яме. Какова вероятность нахождения частицы в средней трети ящика.
Решение

задача 19499

Определить вероятность обнаружения частицы в первой трети одномерного прямоугольного "потенциального ящика" шириной l с бесконечно высокими "стенками", если частица находится в основном состоянии.
Решение

задача 19521

Микрочастица находится в одномерной бесконечно глубокой потенциальной яме шириной l, имея минимальную энергию. Во сколько раз отличаются вероятности обнаружения частицы на отрезке шириной l/4, если этот отрезок лежит: 1. В середине ямы, 2. На краю ямы? Поясните смысл полученного результата графически.
Решение

задача 20664

Электрон находится в одномерном бесконечно глубоком потенциальном ящике шириной l. Вычислить наименьшую разность двух соседних энергетических уровней (в электрон-вольтах) электрона в двух случаях: 1) l = 10 см; 2) l = 1 нм.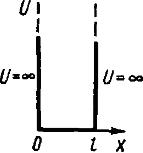
Решение

задача 20695

Используя соотношение неопределенностей, оценить ширину l одномерного потенциального ящика, в котором минимальная энергия Emin.
Решение

задача 20974

Определить при какой ширине потенциальной ямы L дискретность энергии становится сравнимой с энергией теплового движения kТ.
Решение

задача 21056

Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. Определить вероятность обнаружения частицы в пределах от 0 до l/3.
Решение

задача 21086

Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на первом возбужденном уровне. В каких точках ямы плотность вероятности обнаружения частицы максимальна?
Решение

задача 21099

Частица находится в одномерной прямоугольной потенциальной яме шириной а = 3·10–9 м с бесконечными стенками. Волновая функция микрочастицы имеет вид ψ = Asin(8πx/a). Найти максимальное расстояние между точками (в нм), в которых вероятность обнаружения частицы максимальна.
Решение

задача 21305

Микрочастица с массой m находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками шириной а. Разрешенные значения энергии микрочастицы определяются формулой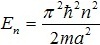 , где n = 1,2,3... Находясь в основном состоянии, микрочастица поглотила фотон с энергией Е = 45 эВ и перешла на четвертый энергетический уровень. Найти наименьший импульс фотона, который может быть излучен этой частицей.
а) 3,1·10–26 кг·м/с; б) 2,5·10–26 кг·м/с; в) 2,1·10–26 кг·м/с;
г) 1,5·10–26 кг·м/с; д) 1,1·10–26 кг·м/с.
Решение

задача 21375

Электрон находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Какова вероятность обнаружения электрона в средней трети ямы, если электрон находится в первом возбуждённом состоянии (n = 2)? Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.
Решение

задача 21829

Электрон движется в одномерной бесконечно глубокой потенциальной яме шириной 0,6 нм, имея энергию 16,6 эВ. Какова вероятность обнаружения этого электрона в первой четверти ямы?
Решение

задача 21862

Частица массы m находится в основном состоянии в одномерной потенциальной яме шириной l с бесконечно высокими стенками. Найти силу давления, которую оказывает частица на стенку.
Решение

задача 21879

Волновая функция частицы массой m для основного состояния в одномерном потенциальном поле U(x) = k·x2/2 имеет вид ψ(x) = A·exp(–α·x2), где A и α — некоторые постоянные. Найти с помощью уравнения Шредингера постоянную α и энергию частицы в этом состоянии.
Решение

задача 21880

Частица находится в прямоугольном одномерном потенциальном ящике с бесконечно высокими стенками в основном состоянии. Какова вероятность обнаружения частицы в крайней трети ящика?
Решение

задача 21984

Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найдите ширину ямы, если минимальное энергетическое расстояние между уровнями электрона в яме равно тепловой энергии KT при комнатной температуре.
Решение

задача 22091

Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина L ямы такова, что энергетические уровни расположены весьма густо. Найти плотность уровней ΔN/ΔE, т. е. их число на единичный интервал энергии в зависимости от Е. Вычислить ΔN/ΔE для Е = 1 эВ, если L = 1 см.
Решение

задача 22096

Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях одномерной потенциальной ямы, ширина которой L, в интервале 0<х<L/4.
Решение

задача 22107

Частица, находящаяся в бесконечно глубоком потенциальном ящике шириной а, находится в возбужденном состоянии с n = 7. Определить вероятность нахождения частицы в центральной трети ящика.
Решение

задача 22122

Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном "ящике" шириной l. Вычислите вероятность того, что электрон, находящийся в возбужденном состоянии n = 3, будет обнаружен в интервале 0<x<(2/3)l.
Решение

задача 22475

Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной 1,5 нм. Найдите плотность вероятности нахождения электрона в тех точках, где она одинакова для электронов, находящихся на первом и втором энергетических уровнях.
Решение

задача 22489

Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Найдите вероятность обнаружить частицу в области l/3 < х < 2l/3. Сравните её с вероятностью обнаружить классическую частицу в этой же области.
Решение

задача 22828

Используя соотношение неопределенностей найти выражение, позволяющее оценить минимальную энергию протона, находящегося в одномерном потенциальном ящике шириной 1 мкм.
Решение

задача 22858

Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. На сколько процентов отличаются энергии двух соседних уровней, если a) n = 3, б) n = 10, в) n = 100.
Решение

задача 23173

Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях в интервале Δx = l/4 равноудаленном от стенок одномерной потенциальной ямы шириной l. Поясните смысл полученного результата графически.
Решение

задача 23210

Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти ширину ямы, если разность энергий между уровнями с n = 2 и n = 3 составляет 0,3 эВ.
Решение

задача 23442

Частица находится в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками". Найти массу частицы, если ширина ямы l = 2,5 нм, а разность энергий 3-го и 2-го энергетических уровней ΔЕ = 0,30 эВ.
Решение

задача 23565

Электрон находится в потенциальном ящике с бесконечно высокими стенками (металл), размеры которого около 1 см. Какую минимальную энергию нужно сообщить электрону для перехода из основного состояния на второй (возбужденный электрон) энергетический уровень (те = 9,1·10–31 кг).
Решение

задача 23710

С помощью соотношения неопределенностей оцените минимальную энергию E1, которой может обладать частица массы m, находящаяся в бесконечно глубокой одномерной потенциальной яме шириной a.
Решение

задача 23719

Частица находится в прямоугольном одномерном потенциальном ящике с бесконечно высокими стенками в основном состоянии. Какова вероятность обнаружения частицы: а) в средней трети ящика; б) в крайней трети ящика?
Решение

задача 23889

Частица находится в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками". Ширина ямы — l. Состояние частицы описывается главным квантовым числом n. Определить: 1) вероятность нахождения частицы в области "ямы" Δ l = x2–x1; 2) точки интервала [х1, х2], в которых плотность вероятности существования частицы максимальна и минимальна. n = 1, x1 = 0,4l, x2 = 0,9l.
Решение

задача 24092

Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном "ящике" шириной l. Вычислите вероятность того, что электрон, находящийся в возбужденном состоянии n = 4, будет обнаружен в интервале (1/4) l<x<(3/4) l.
Решение

задача 24480

В бесконечно глубокой одномерной потенциальной яме шириной l = 792 пм находится электрон в первом возбужденном состоянии. Электрону дополнительно сообщили энергию 7,2 эВ. Как в результате этого изменится плотность вероятности обнаружения электрона в точке х = l/4 потенциальной ямы?
Решение

задача 80307

Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l в основном состоянии. В каких точках ямы плотность вероятности обнаружения частицы максимальна, а в каких — минимальна?
Решение

задача 80307

Частица в бесконечно глубоком одномерном потенциальном ящике шириной l находится в основном состоянии. Найти точки ящика, в которых плотность вероятности обнаружения частицы максимальна, а в каких — минимальна?
Решение